[NOI1999] 棋盤分割(推式子+dp)
阿新 • • 發佈:2017-10-12
blog ron 一個 form div include arch stream images

原棋盤上每一格有一個分值,一塊矩形棋盤的總分為其所含各格分值之和。現在需要把棋盤按上述規則分割成n塊矩形棋盤,並使各矩形棋盤總分的均方差最小。
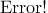 ,其中平均值
,其中平均值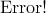 ,xi為第i塊矩形棋盤的總分。
,xi為第i塊矩形棋盤的總分。
請編程對給出的棋盤及n,求出O‘的最小值。
第2行至第9行每行為8個小於100的非負整數,表示棋盤上相應格子的分值。每行相鄰兩數之間用一個空格分隔。 
http://poj.org/problem?id=1191
棋盤分割| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 15655 | Accepted: 5556 |
Description
將一個8*8的棋盤進行如下分割:將原棋盤割下一塊矩形棋盤並使剩下部分也是矩形,再將剩下的部分繼續如此分割,這樣割了(n-1)次後,連同最後剩下的矩形棋盤共有n塊矩形棋盤。(每次切割都只能沿著棋盤格子的邊進行)
原棋盤上每一格有一個分值,一塊矩形棋盤的總分為其所含各格分值之和。現在需要把棋盤按上述規則分割成n塊矩形棋盤,並使各矩形棋盤總分的均方差最小。
請編程對給出的棋盤及n,求出O‘的最小值。
Input
第1行為一個整數n(1 < n < 15)。第2行至第9行每行為8個小於100的非負整數,表示棋盤上相應格子的分值。每行相鄰兩數之間用一個空格分隔。
Output
僅一個數,為O‘(四舍五入精確到小數點後三位)。Sample Input
3 1 1 1 1 1 1 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0 3
Sample Output
1.633
Source
Noi 99
/* 設f(i,a,b,c,d)表示切第i刀,剩余的矩形左上角和右下角的坐標是(a,b)和(c,d), 除了剩余部分其它部分的xi平方和的最小值。 那麽f(i)可以向f(i+1)轉移,只需要暴力枚舉第i+1刀從哪裏切了一刀即可。 */ #include <iostream> #include <cstdio> #include <cmath> using namespace std; const int inf=1<<30;int n, chess[9][9],sum[9][9],dp[9][9][9][9][15]; int getX(int y1, int x1, int y2, int x2) { int a=sum[y2][x2]-sum[y2][x1-1]-sum[y1-1][x2]+sum[y1-1][x1-1]; return a*a; } int main() { scanf("%d", &n); for(int i=1; i<=8; i++) for(int j=1; j<=8; j++) scanf("%d", &chess[i][j]); for(int i=1; i<=8; i++) { for(int j=1; j<=8; j++) sum[i][j]=sum[i][j-1]+chess[i][j]; for(int j=1; j<=8; j++) sum[i][j]+=sum[i-1][j]; } for(int i1=1; i1<=8; i1++) for(int j1=1; j1<=8; j1++) for(int i2=i1; i2<=8; i2++) for(int j2=j1; j2<=8; j2++) dp[i1][j1][i2][j2][0]=getX(i1, j1, i2, j2); for(int i=1; i<n; i++) for(int i1=1; i1<=8; i1++) for(int j1=1; j1<=8; j1++) for(int i2=i1; i2<=8; i2++) for(int j2=j1; j2<=8; j2++) { dp[i1][j1][i2][j2][i]=inf; //左右切割 for(int k=j1; k<j2; k++) dp[i1][j1][i2][j2][i]=min(dp[i1][j1][i2][j2][i], min(dp[i1][j1][i2][k][i-1]+dp[i1][k+1][i2][j2][0], dp[i1][j1][i2][k][0]+dp[i1][k+1][i2][j2][i-1])); //上下切割 for(int k=i1; k<i2; k++) dp[i1][j1][i2][j2][i]=min(dp[i1][j1][i2][j2][i], min(dp[i1][j1][k][j2][i-1]+dp[k+1][j1][i2][j2][0], dp[i1][j1][k][j2][0]+dp[k+1][j1][i2][j2][i-1])); } printf("%d\n",dp[1][1][8][8][n-1]); return 0; }
[NOI1999] 棋盤分割(推式子+dp)
