矩陣乘法的理解(轉)
大多數人在高中,或者大學低年級,都上過一門課《線性代數》。這門課其實是教矩陣。

剛學的時候,還蠻簡單的,矩陣加法就是相同位置的數字加一下。
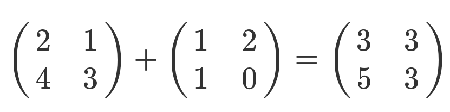
矩陣減法也類似。
矩陣乘以一個常數,就是所有位置都乘以這個數。
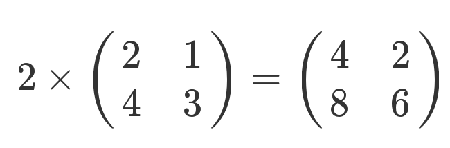
但是,等到矩陣乘以矩陣的時候,一切就不一樣了。
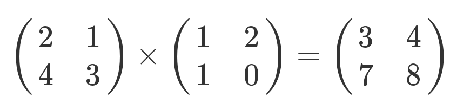
這個結果是怎麽算出來的?
教科書告訴你,計算規則是,第一個矩陣第一行的每個數字(2和1),各自乘以第二個矩陣第一列對應位置的數字(1和1),然後將乘積相加( 2 x 1 + 1 x 1),得到結果矩陣左上角的那個值3。
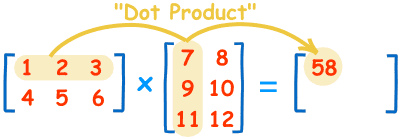
也就是說,結果矩陣第m行與第n列交叉位置的那個值,等於第一個矩陣第m行與第二個矩陣第n列,對應位置的每個值的乘積之和。
怎麽會有這麽奇怪的規則?
我一直沒理解這個規則的含義,導致《線性代數》這門課就沒學懂。研究生時發現,線性代數是向量計算的基礎,很多重要的數學模型都要用到向量計算,所以我做不了復雜模型。這一直讓我有點傷心。
前些日子,受到一篇文章的啟發,我終於想通了,矩陣乘法到底是什麽東西。關鍵就是一句話,矩陣的本質就是線性方程式,兩者是一一對應關系。如果從線性方程式的角度,理解矩陣乘法就毫無難度。
下面是一組線性方程式。
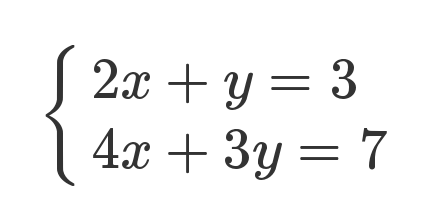
矩陣的最初目的,只是為線性方程組提供一個簡寫形式。
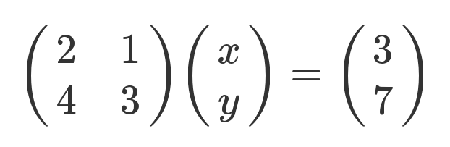
老實說,從上面這種寫法,已經能看出矩陣乘法的規則了:系數矩陣第一行的2和1,各自與 x 和 y 的乘積之和,等於3。不過,這不算嚴格的證明,只是線性方程式轉為矩陣的書寫規則。
下面才是嚴格的證明。有三組未知數 x、y 和 t,其中 x 和 y 的關系如下。
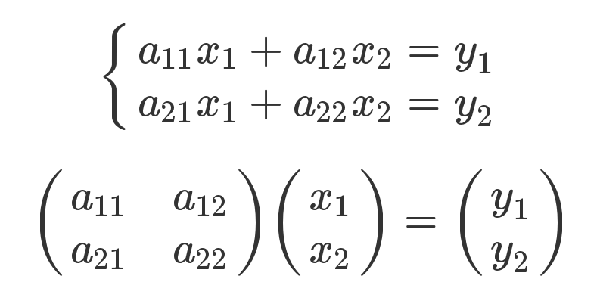
x 和 t 的關系如下。
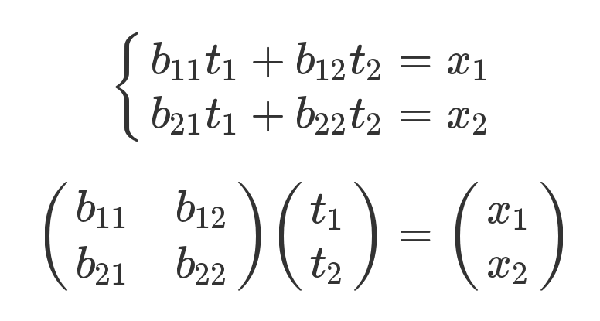
有了這兩組方程式,就可以求 y 和 t 的關系。從矩陣來看,很顯然,只要把第二個矩陣代入第一個矩陣即可。
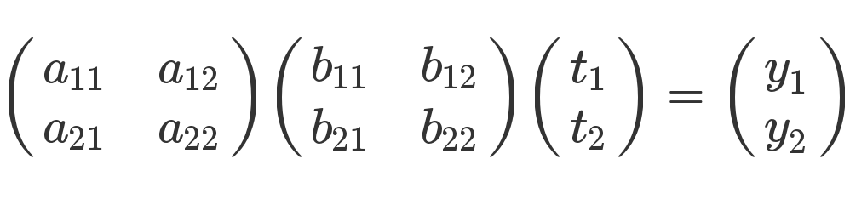
從方程式來看,也可以把第二個方程組代入第一個方程組。
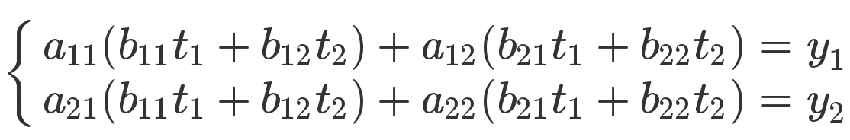
上面的方程組可以整理成下面的形式。
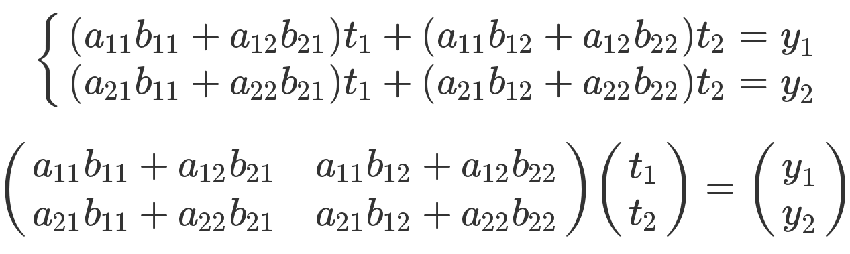
最後那個矩陣等式,與前面的矩陣等式一對照,就會得到下面的關系。
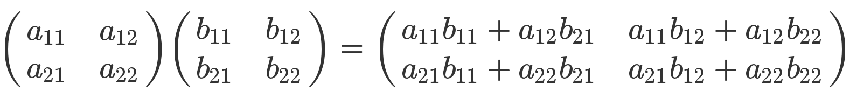
矩陣乘法的計算規則,從而得到證明。
矩陣乘法的理解(轉)
