子集生成算法
阿新 • • 發佈:2017-10-15
輸入 ges 集合 clas n) int for iostream []
原創、轉載請註明出處
給定一個集合(沒有重復元素),輸出所有子集。
首先考慮1~n的所有子集:
為了不出現{1,2}和{2,1}的情況,采用定序的方法。想象一棵解答樹,子節點的元素一定比父節點大。因為定序,解答樹葉子結點的深度不同。
解答樹上的每一個結點有個值,從根節點到葉子結點路徑上的結點值為一個集合,每加一個結點就輸出一次。
代碼如下(輸入n):
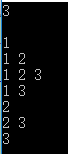
#include<iostream> using namespace std; void f(int A[], int cur, int n) { for(int i = 1; i < cur; i ++) { cout<< A[i] << ‘ ‘; } cout << endl; for(int i = A[cur - 1] + 1; i <= n; i ++) { A[cur] = i; f(A, cur + 1, n); } } int main() { int n; cin >> n; int A[1000]; A[0] = 0; f(A, 1, n); return 0; }
對於任意集合S,把上面的1~n當作鍵值(下標)就可以了(輸入n和S):

#include<iostream> using namespace std; void f(int S[], int A[], int cur, int n) { for(int i = 1; i < cur; i ++) { cout << S[A[i]] << ‘ ‘; } cout << endl; for(int i = A[cur - 1] + 1; i <= n; i ++) { A[cur] = i; f(S, A, cur+ 1, n); } } int main() { int n; cin >> n; int S[1000],A[1000]; for(int i = 1; i <= n; i ++) { cin >> S[i]; } A[0] = 0; f(S, A, 1, n); return 0; }
關鍵點:定序、一個結點代表一個子集
子集生成算法
