2. 程式人生 > >Code VS 1002 搭橋

Code VS 1002 搭橋

阿新 • • 發佈：2017-10-21
return 方法 input 技術 區域 pri 距離 [] log

題目描述 Description

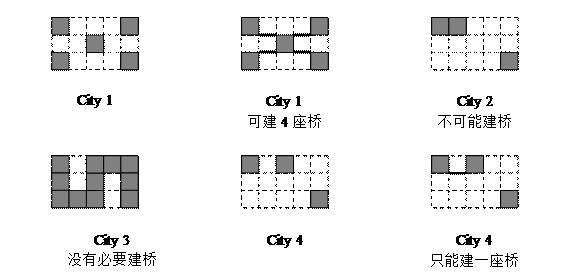
有一矩形區域的城市中建築了若幹建築物，如果某兩個單元格有一個點相聯系，則它們屬於同一座建築物。現在想在這些建築物之間搭建一些橋梁，其中橋梁只能沿著矩形的方格的邊沿搭建，如下圖城市1有5棟建築物，可以搭建4座橋將建築物聯系起來。城市2有兩座建築物，但不能搭建橋梁將它們連接。城市3只有一座建築物，城市4有3座建築物，可以搭建一座橋梁聯系兩棟建築物，但不能與第三座建築物聯系在一起。

技術分享

輸入描述 Input Description

在輸入的數據中的第一行包含描述城市的兩個整數r 和c, 分別代表從北到南、從東到西的城市大小(1 <= r <= 50 and 1 <= c

<= 50). 接下來的r 行, 每一行由c 個(“#”)和(“.”)組成的字符. 每一個字符表示一個單元格。“#”表示建築物，“.”表示空地。

輸出描述 Output Description

在輸出的數據中有兩行，第一行表示建築物的數目。第二行輸出橋的數目和所有橋的總長度。

樣例輸入 Sample Input

樣例1

3 5

#...#

..#..

#...#

樣例2

3 5

##...

.....

....#

樣例3

3 5

#.###

#.#.#

###.#

樣例4:

3 5

#.#..

.....

....#

樣例輸出 Sample Output

樣例1

5

4 4

樣例2

2

0 0

樣例3

1

0 0

樣例4

3

1 1

-----------------------------------------------------------------------------------------------------------------（分割線）

弄了幾乎快2個半小時..............

主要是在建圖上.......................

一開始居然連題目都看不懂.....

￥%&%#@……%&&%￥%......

思路：

這題，主要是dfs+最小生成樹，算法是簡單.....但建圖不好建。

這題第一問很明顯是求聯通塊的個數。

第二問是要求最小生成樹，邊及其長度總和。

因為聯通塊不是一個整體，所以需要做的事是求每個聯通塊間的最小距離。

這裏說兩種方法。

第一種，開四重循環，枚舉點對，然後每次都更新聯通塊間的最小距離。

第二種，掃描法，枚舉每一個城市點，然後以六個方向進行掃描（聽著代碼長度就不會少），然後每次掃描都更新某兩聯通塊間的距離。

　　　　假設當前枚舉的點是（x,y) , 則這六個方向為： （x,i）,(x+1,i) (x-1,i) ,(y,i),(y+1,i),(y-1,i），每次掃描到和當前點的聯通塊編號不相等的點時就更新最小距離。

我用的是第二種，覺得第一種沒挑戰性...........

下面代碼的g[i][j]表示聯通塊編號i與聯通塊編號為j的最小距離。

有問題留言。

#include<cstdio>
#include<cstring>
#include<algorithm>
#define N 60
#define M 250900
using namespace std;

int G[N][N];                //圖數組 

int en,n,r,c;            //邊數，聯通塊個數，題目所描述的，r,c。 


struct edge{
    int s,e,d;
}ed[M];

bool operator < (const edge &a, const edge &b){            //重載運算符 
    return a.d < b.d;
}

void add_edge(int s,int e,int d){                //建邊 
    en++;
    ed[en].s= s,ed[en].e =e ,ed[en].d = d;
}
int fa[M];

int getf(int now){                        //並查集 
    if(now == fa[now])return now;
    else return fa[now] = getf(fa[now]);
}

void kruskal(){                        //kruskal算法 
    sort(ed+1,ed+en+1);
    for(int a = 1; a <= n; a++)fa[a] = a;
    int ans = 0,num = 0;
    for(int a = 1; a <= en; a++){
        int f1 = getf(ed[a].s);
        int f2 = getf(ed[a].e);
        if(f1 != f2){
            fa[f1] = f2;
            ans += ed[a].d;
            num++;
        }
    }
    printf("%d %d\n",num,ans);
}


int tx[] = {0,0,1,1,-1,-1,1,-1};
int ty[] = {1,-1,1,-1,1,-1,0,0};

void dfs(int x,int y){                //求聯通塊 
    G[x][y] = n;
    for(int i = 0; i < 8; i++){
        int xx = tx[i]+x;
        int yy = ty[i]+y;
        if(xx >= 1 && xx <= r && yy >= 1 && yy <= c && (G[xx][yy] == -1))
            dfs(xx,yy);
    }
}


int g[1009][1009];
 
void cread(int x,int y){            //將六個方向再細分，變成十二個方向（笑...） 
    int xx,yy;
    xx = x+1,yy = y+1;;
    while(xx >= 1 && xx <= r && yy >= 1 && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != 0)g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],yy-y-1);
        yy++;
    }
    yy = y-1;
    while(xx >= 1 && xx <= r && yy >= 1 && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != 0)g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],y-yy-1);
        yy--;
    }
    xx = x,yy = y+1;
    while(xx >= 1 && xx <= r && yy >= 1 && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != 0)g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],yy-y-1);
        yy++;
    }
    yy = y-1;
    while(xx >= 1 && xx <= r && yy >= 1 && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != 0)g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],y-yy-1);
        yy--;
    }
    xx = x-1,yy = y+1;
    while(xx >= 1 && xx <= r && yy >= 1 && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != 0)g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],yy-y-1);
        yy++;
    }
    yy = y-1;
    while(xx >= 1 && xx <= r && yy >= 1 && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != 0)g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],y-yy-1);
        yy--;
    }
    
    yy = y,xx = x+1;
    while(xx >= 1 && xx <= r && yy >= 1 && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != 0)g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],xx-x-1);
        xx++;
    }
    xx = x-1;
    while(xx >= 1 && xx <= r && yy >= 1 && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != 0)g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],x-xx-1);
        xx--;
    }
    yy = y+1,xx = x+1;
    while(xx >= 1 && xx <= r && yy >= 1 && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != 0)g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],xx-x-1);
        xx++;
    }
    xx = x-1;
    while(xx >= 1 && xx <= r && yy >= 1 && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != 0)g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],x-xx-1);
        xx--;
    }
    yy = y-1;xx = x+1;
    while(xx >= 1 && xx <= r && yy >= 1 && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != 0)g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],xx-x-1);
        xx++;
    }
    xx = x-1;
    while(xx >= 1 && xx <= r && yy >= 1 && yy <= c && (G[xx][yy] != G[x][y])){
        if(G[xx][yy] != 0)g[G[x][y]][G[xx][yy]] = min(g[G[x][y]][G[xx][yy]],x-xx-1);
        xx--;
    }
}

int main(){
    scanf("%d%d",&r,&c);
    for(int i = 1; i <= r; i++){
        char s[55];
        scanf("%s",s);
        for(int j = 0; j < c; j++)
            if(s[j] == ‘#‘)G[i][j+1] = -1;
            else G[i][j+1] = 0;
    }
    for(int i = 1; i <= r; i++){
        for(int j = 1; j <= c; j++){
            if(G[i][j] == -1){
                n++;
                dfs(i,j);
            }
        }
    }
    
    memset(g,0x3f,sizeof(g));
    
    printf("%d\n",n);
    for(int i = 1; i <= r; i++)
      for(int j = 1; j <= c; j++)
         if(G[i][j] != 0)cread(i,j);
    
    for(int i = 1; i <= n; i++)
       for(int j = 1; j <= n; j++)
          if(g[i][j] != g[0][0])add_edge(i,j,g[i][j]);
    kruskal();
    return 0;
}

Code VS 1002 搭橋

相關推薦

Code VS 1002 搭橋

return 方法 input 技術 區域 pri 距離 [] log 題目描述 Description 有一矩形區域的城市中建築了若幹建築物，如果某兩個單元格有一個點相聯系，則它們屬於同一座建築物。現在想在這些建築物之間搭建一些橋梁，其中橋梁只能沿著矩形的方格的邊沿搭

區間DP code[vs]1258 關路燈

兩個 輸出 sample flask cst ostream 所有 %d 整數 1258 關路燈 時間限制: 1 s 空間限制: 128000 KB 題目等級 : 大師 Master 題目描述 Descriptio

codevs 1002 搭橋

clu style edi fin int operator ans 輸入 pri 題目描述 Description 有一矩形區域的城市中建築了若幹建築物，如果某兩個單元格有一個點相聯系，則它們屬於同一座建築物。現在想在這些建築物之間搭建一些橋梁，其

code vs 1245 最小的N個和

ace define efault cnblogs http 兩個 ble 輸入一個正整數n all 1245 最小的N個和 時間限制: 1 s 空間限制: 128000 KB 題目等級 : 鉆石 Diamond

code vs 1216 跳馬問題

image tab nbsp cor 一個 總數 phy mut ack 1216 跳馬問題 時間限制: 1 s 空間限制: 128000 KB 題目等級 : 黃金 Gold 題解

[CODE[VS]] P2188 最長上升子序列

std lis ++ 2個 兩個 整數 spa post 滿足 題目描述 Description LIS問題是最經典的動態規劃基礎問題之一。如果要求一個滿足一定條件的最長上升子序列，你還能解決嗎？ 給出一個長度為N整數序列，請求出它的包含第K個元素的最長上升子序列。

CODE[VS] 2008 你已經愛我多久了

hint code BE fin AD min names -m mon 題目描述 Description 小A和小B是一對情侶，並且他們都喜歡數學。向其他戀愛中的女孩一樣，小B總是喜歡問小A一些奇怪的問題。 今天，小B問小A：“你已經愛我多久了。&r

CODE[VS] 2692 小明過生日

opened 輸入 stream 就是 iostream 小明 TP put AD 題目描述 Description 今天是小明的生日，請問下一個生日在什麽時候.格式：年 月 日。 輸入描述 Input Description 小明的生日

CODE[VS] 3411 洪水

bfs gif 100% using dfs AI fault 是否 bfc 題目描述 Description 小浣熊松松和朋友到野外露營，沒想到遇上了&pi;年一次的大洪水，好在松松是一只愛觀察的小浣熊，他發現露營地的地形和洪水有如下性質： ①露營地可

CODE[VS] 3164 質因數分解

AC def tro esp efault color pri NPU 難度 題目描述 Description （多數據）給出t個數，求出它的質因子個數。 數據沒坑，難度降低。 輸入描述 Input Description 第一行 t

P1887 乘積最大3 || CODE [VS] 3370 乘積最大3

badge printf 最小 AC 問題 輸出 方案 一行 space 題目描述 請你找出M個和為N的正整數，他們的乘積要盡可能的大。 輸出字典序最小的一種方案。 輸入輸出格式 輸入格式： 一行，兩個正整數N,M 輸出格式： M個和為N的

CODE[VS] 1470 數列處理

des ace 思路 ted script sort rip fault png 題目描述 Description 輸入一列整數，輸出它們的總和、最大值、最小值、並從大到小輸出。 輸入描述 Input Description 第1行：一個

CODE[VS] 2221 搬雕像 ——2011年臺灣高級中學咨詢學科能力競賽

struct 競賽 分享圖片 fault 真的 abs tex 一次 -s 題目描述 Description 王先生是一位收藏家，他收集了非常多有名的雕像。某天，為了美觀，他想要將收藏臺上的雕像按照某種方式重新擺放，由於雕像都有一定的重量，所以他決定雇用一位年輕人，小

CODE[VS] 2664 上廁所

spa 整數 排除 ret 輸出 src 分鐘 can 就會 題目描述 Description 李宸同學在離下課k分鐘的時候想要上廁所，已知只要他憋超過60分鐘，他就會憋死，下課了，廁所有n個坑，每個坑都有人，求李宸同學能否在60分鐘內上到廁所若能打印&ldquo

code[vs] 3500 快速冪入門

blank problem image 一切都 code 應該 分享 () pri 3500 快速冪入門 題目描述 Description 輸入3個數a,b,c，求a^b mod c=? 輸入描述 Input Description 三

CODE[VS] 1262 不要把球傳我

ace 輸入一個整數 一切都 cstring rip cst 循環 一行 mat 題目描述 Description CCC的足球比賽和傳統的足球比賽有一點不同， 一次進球當且僅當先後接觸到球的4名隊員的球衣編號是升序排列的。 球員的球衣編號從過1到99，並且每個

CODE[VS] 1502 這個月有幾天

out hint sin src span inf IT www 技術 題目描述 Description 輸入一個年代和一個月份，打印該月的天數 輸入描述 Input Description 一個年代和一個月份 輸出描述 O

CODE[VS] 1860 最大數 1998年NOIP全國聯賽提高組

body all 真的 題目 class namespace nbsp out tro 題目描述 Description 　　設有n個正整數（n≤20），將它們聯接成一排，組成一個最大的多位整數。 輸入描述 Input Description

CODE[VS] 2951 打字比賽

double esp 簡單的 struct 分享圖片 ane 如果 輸出 fault 題目描述 Description 樂樂學習編程有兩年之久，練就了過硬的指法，打字速度超快，他被選拔代表班級參加校園文化周活動之漢字錄入比賽。 比賽規則：組織方提供一篇文章，利用

CODE[VS] 1621 混合牛奶 USACO

牛奶 mes () 整數 inpu rip break 等於 names 題目描述 Description 牛奶包裝是一個如此低利潤的生意,所以盡可能低的控制初級產品(牛奶)的價格變的十分重要.請幫助快樂的牛奶制造者(Merry Milk Makers)以可能的最