題面在最下方。

首先最短路判斷一下有沒有輸出 -1 的情況。

然後把握答案可以二分求解的特點，那就很容易解決了。

令邊中最大的年代為 maxx

那麽就在[1,maxx]中進行二分求解，枚舉年代mid，跑一遍最短路，不走年代<=mid的邊，然後判斷dis[n]是否>=T，如果>=說明mid可能偏大，否則mid可能偏小。

怎麽優化？

把所有邊的年代存下來，sort一次，然後在這些數據裏面二分（mid只能是出現過的年代）。

優化你的最短路算法，例如SPFA的LLL優化與SLF優化

二分暴力求解即可。

 1 #include<cstdio>
 2 #include<cstring>
 3
 
 #include<algorithm>
 4 using namespace std;
 5 template<class T> inline void read(T &_a){
 6     int _ch=getchar();_a=0;
 7     while(_ch<‘0‘ || _ch>‘9‘)_ch=getchar();
 8     while(_ch>=‘0‘ && _ch<=‘9‘){_a=(_a<<1)+(_a<<3)+_ch-‘0‘;_ch=getchar();}
 9 }
10 
11
 
 const int maxn=20001,maxm=100001;
12 int n,m,T,egcnt,head[maxn],q[maxn],dis2[maxn],dis[maxn],tail,h,maxx;
13 bool ins[maxn],vis[maxn];
14 struct edge{
15     int next,to,dis,year;
16 }w[maxm<<1];
17 
18 inline void addedge(int from,int to,int dis,int year)
19 {
20     w[++egcnt].dis=dis;
21     w[egcnt].to=to;
 
22     w[egcnt].year=year;
23     w[egcnt].next=head[from];
24     maxx=max(maxx,year);
25     head[from]=egcnt;
26 }
27 
28 inline void spfa(int y){
29     memset(dis,0x7f,sizeof(dis));
30     dis[1]=0; q[1]=1; h=0; tail=1;
31     while(h!=tail)
32     {
33         h=h%20000+1;
34         int now=q[h];
35         ins[now]=false;
36         for (register int i=head[now];i;i=w[i].next)
37          if(w[i].year>y){
38             if(dis[w[i].to]>dis[now]+w[i].dis)
39             {
40                 dis[w[i].to]=dis[now]+w[i].dis;
41                 if(!ins[w[i].to])
42                 {
43                     ins[w[i].to]=true;
44                     tail=tail%20000+1;
45                     q[tail]=w[i].to;
46                 }
47             }
48         }
49     }
50 }
51 
52 int main()
53 {
54     read(n); read(m); read(T);
55     for (register int i=1,s,t,l,y;i<=m;++i) read(s),read(t),read(l),read(y),addedge(s,t,l,y);
56     spfa(0);
57     if(dis[n]>=T) { printf("-1 %d",dis[n]); return 0; }
58     int l=1,r=maxx;
59     while(l<=r)
60     {
61         memset(vis,0,sizeof(vis));
62         int mid=l+r>>1;
63         spfa(mid);
64         if(dis[n]<T) l=mid+1;
65          else r=mid-1;
66     }
67     printf("%d",r+1);
68     return 0;
69 }

【題目描述】由於A學校生物實驗室裏那個不負責的數據分析員，實驗室的病毒威力被錯誤估算，導致了可怕的病毒泄漏，現在病毒即將在校園內傳播開來。校園裏一共有n個建築物，生物實驗室總是位於一號建築物且在0時刻受到病毒入侵。這n個建築物由m條單向道路相連（也有可能有建築物被孤立）。每條道路有兩個信息：它的長度，它是多少年前修建的。當一個建築物被病毒入侵，從被入侵的時刻起，病毒會從所有由這個建築物通向其他建築物的道路按著這條道路的方向以1個單位每秒的速度行進。校長得知這個事情後，決定放棄這個學校逃跑。校長總是位於編號為n的行政樓，從零時刻開始需要共T秒來逃出行政樓，且逃出行政樓即視為逃出了這個學校。也就是說，如果病毒入侵行政樓的時間不小於T，則校長能夠成功逃離。有些時候，校長沒有足夠的時間逃離，因為病毒到達行政樓的時間太快了。為了讓校長能夠逃離學校，不得不拆除校園內的一些道路以延緩行政樓的被入侵時間（拆除道路視為在0時刻被拆的道路全部消失）。當然，如果使得病毒根本無法到達行政樓，也是可以的。但是，拆除道路會影響學校的歷史氣息，且破壞程度定義為拆除的道路中最古老的一條的年齡。請求出保證校長能夠安全撤離的情況下，最小的破壞程度。

【輸入格式】第一行包含三個整數：n,m,T。接下來m行，每行描述一條有向道路。每行4個整數，si,ti,Li,Yi，分別表示這條道路的起點，終點，長度，這條道路的年齡。

【輸出格式】如果不需要拆除任何道路，輸出一行兩個數：-1和行政樓的被感染時刻（當然這個時刻大於等於T），以空格隔開。否則輸出一行包含一個數：最小的破壞程度。

【輸入樣例一】

5515

12635

24840

13645

34325

45550

【輸出樣例一】

25

【樣例解釋一】

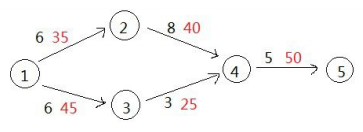
每條邊上的黑字對應這條路的長度，紅字對應年齡。校長將在第15秒逃出學校，如果不拆除任何道路，行政樓將在第14秒受到入侵。你可以拆除4到5的道路，使得行政樓免於入侵，這樣的破壞程度是50。但是最好的方法是拆掉3到4之間的道路，這樣使得行政樓在第19秒受到入侵，校長就可以逃離了。

【輸入樣例二】

3 2 10

1 2 5 30

2 3 6 50

【輸出樣例二】

-1 11

【數據範圍】

對於 60%的數據，n,m<=100.

對於 100%的數據，n<=20000, m<=100000. 數據保證在不拆除任何道路的情況下，從 1 號樓到 n 號樓一定存在路徑。

疫情延遲 NOIP模擬 二分答案 圖論