學習方法 深度學習 變體 復雜 鏈接 線性規劃 con images 叠代

轉自：http://www.cnblogs.com/caocan702/p/5666175.html

借鑒前人的文章鏈接

http://blog.csdn.net/zouxy09/article/details/8777094

http://www.gene-seq.com/bbs/thread-2853-1-1.html

http://ibillxia.github.io/blog/2012/09/26/convex-optimization-overview/

UFLDL教程

http://ufldl.stanford.edu/wiki/index.php/%E7%A8%80%E7%96%8F%E7%BC%96%E7%A0%81

如果我們把輸出必須和輸入相等的限制放松，同時利用線性代數中基的概念，即O = a₁

*Φ₁ + a₂*Φ₂+….+ a_n*Φ_n， Φ_i是基，a_i是系數，我們可以得到這樣一個優化問題：

Min |I – O|，其中I表示輸入，O表示輸出。

通過求解這個最優化式子，我們可以求得系數a_i和基Φ_i，這些系數和基就是輸入的另外一種近似表達。

因此，它們可以用來表達輸入I，這個過程也是自動學習得到的。如果我們在上述式子上加上L1的Regularity限制，得到：

Min |I – O| + u*(|a₁| + |a₂| + … + |a_n |)

這種方法被稱為Sparse Coding。通俗的說，就是將一個信號表示為一組基的線性組合，而且要求只需要較少的幾個基就可以將信號表示出來。“稀疏性”定義為：只有很少的幾個非零元素或只有很少的幾個遠大於零的元素。要求系數 a_i

是稀疏的意思就是說：對於一組輸入向量，我們只想有盡可能少的幾個系數遠大於零。選擇使用具有稀疏性的分量來表示我們的輸入數據是有原因的，因為絕大多數的感官數據，比如自然圖像，可以被表示成少量基本元素的疊加，在圖像中這些基本元素可以是面或者線。同時，比如與初級視覺皮層的類比過程也因此得到了提升（人腦有大量的神經元，但對於某些圖像或者邊緣只有很少的神經元興奮，其他都處於抑制狀態）。

稀疏編碼算法是一種無監督學習方法，它用來尋找一組“超完備”基向量來更高效地表示樣本數據。雖然形如主成分分析技術（PCA）能使我們方便地找到一組“完備”基向量，但是這裏我們想要做的是找到一組“超完備”基向量來表示輸入向量（也就是說，基向量的個數比輸入向量的維數要大）。超完備基的好處是它們能更有效地找出隱含在輸入數據內部的結構與模式。然而，對於超完備基來說，系數a_i

不再由輸入向量唯一確定。因此，在稀疏編碼算法中，我們另加了一個評判標準“稀疏性”來解決因超完備而導致的退化（degeneracy）問題。

比如在圖像的Feature Extraction的最底層要做Edge Detector的生成，那麽這裏的工作就是從Natural Images中randomly選取一些小patch，通過這些patch生成能夠描述他們的“基”，也就是右邊的8*8=64個basis組成的basis，然後給定一個test patch, 我們可以按照上面的式子通過basis的線性組合得到，而sparse matrix就是a，下圖中的a中有64個維度，其中非零項只有3個，故稱“sparse”。

Sparse coding分為兩個部分：

1）Training階段：給定一系列的樣本圖片[x1, x 2, …]，我們需要學習得到一組基[Φ1, Φ2, …]，也就是字典。

稀疏編碼是k-means算法的變體，其訓練過程也差不多（EM算法的思想：如果要優化的目標函數包含兩個變量，如L(W, B)，那麽我們可以先固定W，調整B使得L最小，然後再固定B，調整W使L最小，這樣叠代交替，不斷將L推向最小值。

訓練過程就是一個重復叠代的過程，按上面所說，我們交替的更改a和Φ使得下面這個目標函數最小。

每次叠代分兩步：

a）固定字典Φ[k]，然後調整a[k]，使得上式，即目標函數最小（即解LASSO問題）。見下

b）然後固定住a [k]，調整Φ [k]，使得上式，即目標函數最小（即解凸QP問題）。見下

不斷叠代，直至收斂。這樣就可以得到一組可以良好表示這一系列x的基，也就是字典。

2）Coding階段：給定一個新的圖片x，由上面得到的字典，通過解一個LASSO問題得到稀疏向量a。這個稀疏向量就是這個輸入向量x的一個稀疏表達了。

例如：

LASSO問題

使用數理統計模型從海量數據中有效挖掘信息越來越受到業界關註。在建立模型之初，為了盡量減小因缺少重要自變量而出現的模型偏差，通常會選擇盡可能多的自變量。然而，建模過程需要尋找對因變量最具有強解釋力的自變量集合，也就是通過自變量選擇(指標選擇、字段選擇)來提高模型的解釋性和預測精度。指標選擇在統計建模過程中是極其重要的問題。Lasso算法則是一種能夠實現指標集合精簡的估計方法。 Tibshirani(1996)提出了Lasso(The Least Absolute Shrinkage and Selectionator operator)算法。這種算法通過構造一個懲罰函數獲得一個精煉的模型；通過最終確定一些指標的系數為零，LASSO算法實現了指標集合精簡的目的。這是一種處理具有復共線性數據的有偏估計。Lasso的基本思想是在回歸系數的絕對值之和小於一個常數的約束條件下，使殘差平方和最小化，從而能夠產生某些嚴格等於0的回歸系數，得到解釋力較強的模型。R統計軟件的Lars算法的軟件包提供了Lasso算法。根據模型改進的需要，數據挖掘工作者可以借助於Lasso算法，利用AIC準則和BIC準則精煉簡化統計模型的變量集合，達到降維的目的。因此，Lasso算法是可以應用到數據挖掘中的實用算法。Lasso是一個線性模型，用於評估稀少系數下的數據類型。當參數值較少時Lasso算法非常有用，可以有效降低數據誤差。 　　原始文章在這裏，http://statweb.stanford.edu/~tibs/lasso/lasso.pdf 凸QP問題 在一般情況下，求解任意一個函數的全局最優值是很困難的。但是對於一種特定類型的函數——凸函數（convex function）， 我們可以很有效的求解其全局最優值。這裏的“有效”是指在實際問題求解中，能在多項式復雜度的時間裏求解。 人們將這類函數的最值問題稱為凸優化問題（Convex Optimal Problem）

凸集的定義：一個集合C是凸集，當且僅當對任意x,y∈C和θ∈RR且0≤θ≤1，都有

θx+(1?θ)y∈C. 其幾何意義在於，在集合C中任取兩個點，連接兩點的直線段上的任一點也在集合C中。下圖是凸集和非凸集的例子：

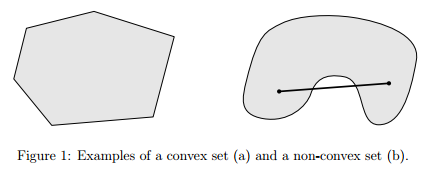
常見的凸集有：n維實數空間；一些範數約束形式的集合；仿射子空間；凸集的並集；n維半正定矩陣集；凸優化中的一個核心概念就是凸函數。

凸函數定義：一個函數f:Rn→R是凸函數當且僅當其定義域（設為D(f)）是凸集， 且對任意的x,y∈D(f)和θ∈R且0≤θ≤1，都有

f(θx+(1?θ)y≤θf(x)+(1?θ)f(y))

設f(x)為一元函數，那麽上式的幾何意義在於，曲線上任意兩點處的割線在函數曲線的上方，常見的凸函數有指數函數（f(x)=ax，a>1）、負對數函數（f(x)=?logax，a>1，x>0）、開口向上的二次函數等。

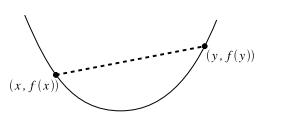
有了凸集和凸函數的定義，現在我們重點討論凸優化問題的求解方法。凸優化的一般描述為：

其中f(x)為凸函數，C是一個凸集，這是不帶約束條件的情況下的凸優化問題。對於帶約束條件的問題而言，其一般描述為：
其中f(x)為凸函數，gi(x)對所有的ii均為凸函數，hj(x)均為仿射函數。註意gi(x)不等式中不等號的方向。

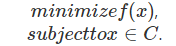
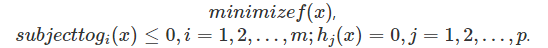
凸問題中的全局優化：首先要分清楚什麽是局部最優，什麽是全局最優。局部最優是指在該最優值附近的點對應的函數值 都比該最優值大，而全局最優是指對可行域裏所有點，其函數值都比該最優值大。對於凸優化問題，它具有一個很重要的特性， 那就是所有的局部最優值都是全局最優的。

（1）線性規劃（Linear Programing, LP）: 目標函數和約束條件函數都是線性函數的情況，一般形式如下：

（2）二次規劃（Quadratic Programing, QP）: 目標函數為二次函數，約束條件為線性函數，一般形式為：

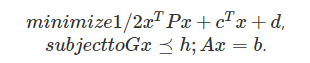
LP可以看做是QP的特例，QP包含LP。

（3）二次約束的二次規劃（Quadratically Constrained Quadratic Programming, QCQP）: 目標函數和約束條件均為 二次函數的情況，QP可以看做是QCQP的特例，QCQP包含QP。

（4）半正定規劃（Semide?nite Programming，SDP）QCQP可以看做是SDP的特例，SDP包含QCQP。SDP在machine learning中有非常廣泛的應用。

凸優化應用舉例

下面我們來看幾個實例。
（1）支持向量機（Support Vector Machines，SVM）：凸優化在machine learning中的一個典型的應用就是基於支持向量機分類器， 它可以用如下優化問題表示：

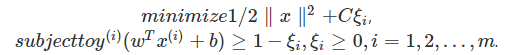
其中決策變量w∈Rn,ξ∈Rn,b∈R. C∈R,x(i),y(i),i=1,2,…,m由 具體問題定義。可以看出，這是一個典型的QP問題。

（2）帶約束的least squares問題：其一般描述為

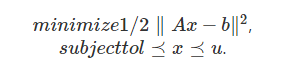
這也是一個很典型的QP問題。

（3）Maximum Likelihood for Logistic Regression：該問題的目標函數為:其中g(z)g(z)為Sigmoid函數，

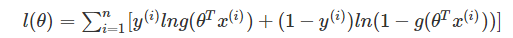
對於凸優化問題，目前沒有一個通用的解析式的 解決方案，但是我們仍然可以用非解析的方法來有效的求解很多問題。內點法被證明是很好的解決方案， 特別具有實用性，在某些問題中，能夠在多項式時間復雜度下，將解精確到指定精度。

《神經網絡與深度學習》（三） 稀疏編碼