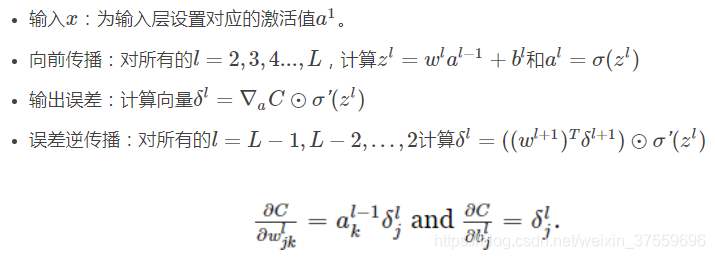神經網路和深度學習(三)—— 反向傳播工作原理
反向傳播演算法工作原理
在上一篇文章,我們看到了神經網路如何通過梯度下降演算法學習,從而改變權重和偏差。但是,前面我們並沒有討論如何計算代價函式的梯度,這是一個很大的遺憾。這一篇文章,我們將介紹一種稱為反向傳播的快速計算梯度的演算法。
使用反向傳播演算法學習的神經網路比其他早期的方法要快很多,這使得使用神經網路可以解決之前不能解決的問題。如今,反向傳播演算法是神經網路中最重要的組成部分。
你完全可以忽略反向傳播演算法,把它當作一個黑盒子去使用神經網路。那麼我們為什需要詳細的瞭解這個演算法呢?這當然是為了理解神經網路的學習過程。反向傳播演算法的核心是一個對於任何權重或者偏差計算其關於代價函式的偏導數的表示式。這個表示式告訴我們改變權重和偏差時,代價函式的變化快慢。雖然這個表示式很複雜,但是它卻有自己的數學之美,每一個元素擁有一個自然的直觀解釋。因此反向傳播不僅僅是為了學習的一個快速演算法,它實際上給了我們一個視角去深入瞭解在改變權重和偏差時,網路整體的行為的變化。這才是我們詳細瞭解反向傳播演算法的意義所在。
熱身: 一種基於矩陣計算神經網路輸出的快速方法
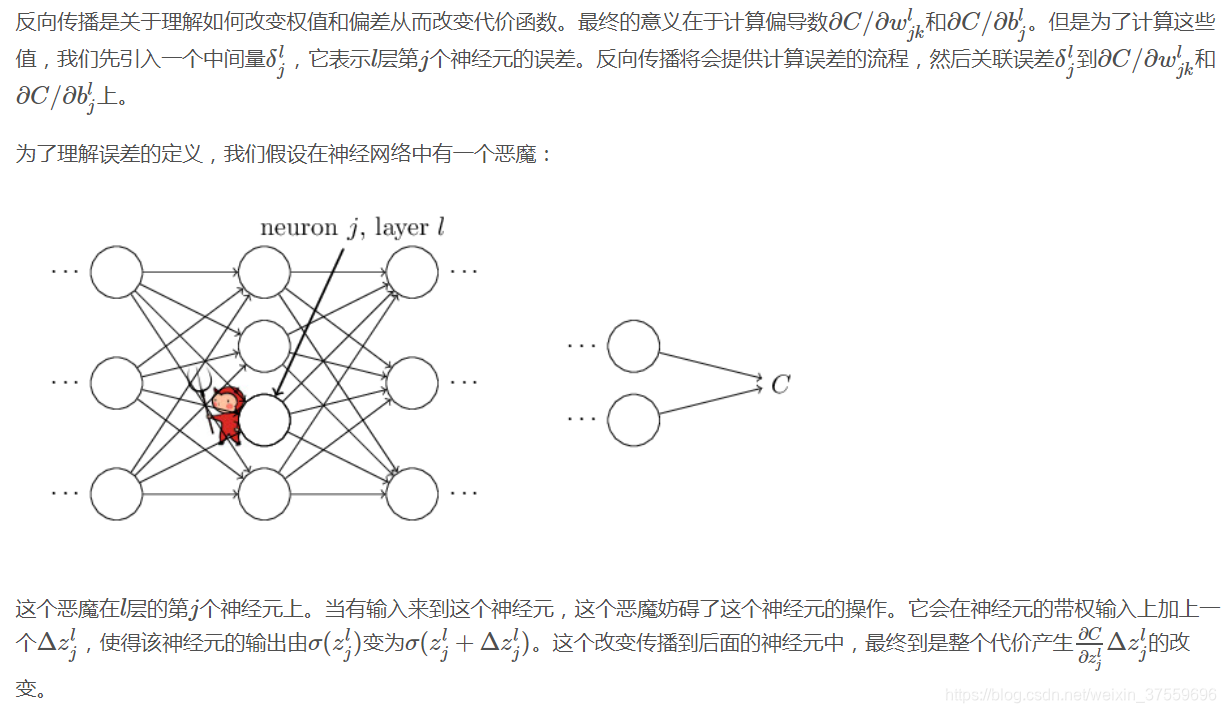
在討論反向傳播演算法之前,我們使用一種基於矩陣的計算神經網路輸出的快速方法來做預熱。這可以讓我們在學習反向傳播時更加熟悉各種記號和表示方法。
這個記號剛開始很繞,需要一點時間熟悉。經過一段時間的掌握一會發現這樣的表達很簡單自然。這個記號很彆扭的地方在於j和k的順序,你可能和我一樣剛開始覺得j和k的位置需要換一下更舒服,但是下面我將告訴你為什麼這樣做。
即,向量化f就是對向量中所有元素進行平方計算。
有了這些定義,公式(23)就可以重寫為下面這個美妙而簡介的向量形式了:
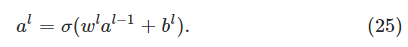
第二個假設是代價可以寫成神經網路輸出的函式:
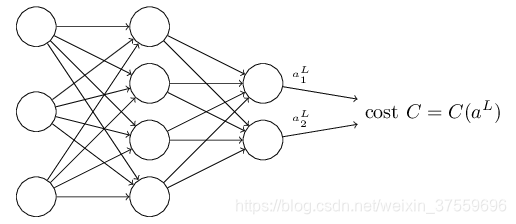
比如,二次代價函式滿足這個需求,因為二次代價函式對一個單個的訓練樣本x可以寫作:
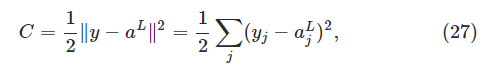

這種按元素乘積的操作有時被稱作Hadamard乘積或者Schur乘積。
反向傳播的四個基本方程
解決方案:反向傳播基於四個基本方程。這些方程給了我們計算誤差δ l δl和代價函式梯度的方法(別忘了我們的目的是計算代價函式關於權重和偏差的梯度,但是這些都是基於計算誤差所求得,後面會講述的很明白)。後面的公式其實不難,你第一眼看上起可能很複雜,當你靜下心看完後面的證明你會覺得這些公式很簡潔,而且用程式碼很容易實現。首先,我們會證明這些公式的正確性,然後以為程式碼的形式給出它們的演算法形式;然後用python程式碼實現它們;在本文的最後,我們會發展出⼀個關於反向傳播⽅程含義的直覺畫⾯,以及人們如何能夠從零開始發現這個規律。
證明:這裡先給出(BP1)的證明(實在是不想用latex敲公式了,直接參考了其他人翻譯的):

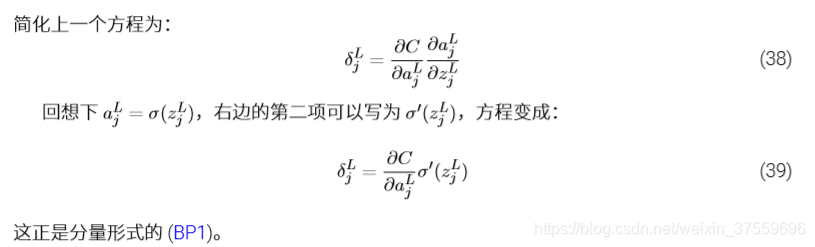

證明:

方程3: 代價函式關於任意偏差的改變率(偏導數)(反向傳播函式的返回值之一):

方程4: 代價函式關於任意權重的改變率(偏導數)(反向傳播函式的返回值之一):

同樣這裡公式右邊的量都可以通過前面的公式求出,上式可以簡寫為:

下面總結一下這四個方程:

反向傳播演算法
反向傳播演算法給出了一種計算代價函式梯度的方法,我們用演算法的形式明確地寫出來:
輸出:代價函式的梯度。
這個演算法是針對一個輸入樣本x時,計算代價函式梯度,但是我們前面講過,我們在標準的梯度下降演算法中,是對所有樣本的梯度值求和取平均,在隨機梯度演算法中我們是對一個小批量資料的梯度值求和取平均。下面假設給定小批量樣本大小為m,則隨機梯度下降演算法為:

程式碼改進:我們對於隨機梯度下降的實現是對⼀ 個小批量資料中的訓練樣本進行遍歷。所以也可以更改反向傳播演算法使得它同時對⼀個小批量資料中的所有樣本進行梯度計算。這個想法其實就是我們可以用⼀個矩陣 X=[x1,x2,…,xm]X=[x1,x2,…,xm],其中每列就是在小批量資料中的向量,而不是單個的輸⼊向量xx。 我們通過乘權重矩陣,加上對應的偏置進行前向傳播,在所有地方應用S型函式。然後按照類似的過程進行反向傳播,這會提高程式碼的速度(在我的膝上型電腦上,在MNIST分類問題上,我相較於上一篇文章的實現獲得了2倍的速度提升)。