線性 實驗 tab 下一個 約束 特征 方式 等於 b2c

『教程』L0、L1與L2範數

一、L0範數、L1範數、參數稀疏

L0範數是指向量中非0的元素的個數。如果我們用L0範數來規則化一個參數矩陣W的話，就是希望W的大部分元素都是0，換句話說，讓參數W是稀疏的。 　　既然L0可以實現稀疏，為什麽不用L0，而要用L1呢？一是因為L0範數很難優化求解（NP難問題），二是L1範數是L0範數的最優凸近似，而且它比L0範數要容易優化求解。所以大家才把目光和萬千寵愛轉於L1範數。

總結：L1範數和L0範數可以實現稀疏，L1因具有比L0更好的優化求解特性而被廣泛應用。

參數稀疏的優點，

1）特征選擇(Feature Selection)：

大家對稀疏規則化趨之若鶩的一個關鍵原因在於它能實現特征的自動選擇。一般來說，x_i

的大部分元素（也就是特征）都是和最終的輸出y_i沒有關系或者不提供任何信息的，在最小化目標函數的時候考慮x_i這些額外的特征，雖然可以獲得更小的訓練誤差，但在預測新的樣本時，這些沒用的信息反而會被考慮，從而幹擾了對正確y_i的預測。稀疏規則化算子的引入就是為了完成特征自動選擇的光榮使命，它會學習地去掉這些沒有信息的特征，也就是把這些特征對應的權重置為0。

2）可解釋性(Interpretability)：

另一個青睞於稀疏的理由是，模型更容易解釋。例如患某種病的概率是y，然後我們收集到的數據x是1000維的，也就是我們需要尋找這1000種因素到底是怎麽影響患上這種病的概率的。假設我們這個是個回歸模型：y=w₁

*x₁+w₂*x₂+…+w₁₀₀₀*x₁₀₀₀+b（當然了，為了讓y限定在[0,1]的範圍，一般還得加個Logistic函數）。通過學習，如果最後學習到的w*就只有很少的非零元素，例如只有5個非零的w_i，那麽我們就有理由相信，這些對應的特征在患病分析上面提供的信息是巨大的，決策性的。也就是說，患不患這種病只和這5個因素有關，那醫生就好分析多了。但如果1000個w_i都非0，醫生不得不面對這1000種因素。

二、L1範數、L2範數

　　L2範數的規則項||W||₂最小，可以使得W的每個元素都很小，都接近於0，但與L1範數不同，它不會讓它等於0，而是接近於0。

L2範數的好處如下，

1）學習理論的角度：

從學習理論的角度來說，L2範數可以防止過擬合，提升模型的泛化能力。

2）優化計算的角度：

從優化或者數值計算的角度來說，L2範數有助於處理 condition number不好的情況下矩陣求逆很困難的問題。

病態條件：

咱們先看左邊的那個，第一行假設是我們的AX=b，第二行我們稍微改變下b，得到的x和沒改變前的差別很大。第三行我們稍微改變下系數矩陣A，可以看到結果的變化也很大。換句話來說，這個系統的解對系數矩陣A或者b太敏感了。

　　因為一般我們的系數矩陣A和b是從實驗數據裏面估計得到的，所以它是存在誤差的，如果我們的系統對這個誤差是可以容忍的還好，但系統對這個誤差太敏感了，我們的解的誤差更大，所以這個方程組系統就是ill-conditioned病態的。

　　右邊那個就叫well-condition的系統了。

condition number：

　　如果方陣A是非奇異的，那麽A的 condition number 定義為：

κ(A)=∥A∥∥A?1∥ κ(A)=∥A∥∥A?1∥

　　如果方陣 A 是奇異的，那麽 A 的 condition number 就是正無窮大了，實際上，每一個可逆方陣都存在一個 condition number。

對condition number來個一句話總結：condition number 是一個矩陣（或者它所描述的線性系統）的穩定性或者敏感度的度量，如果一個矩陣的 condition number 在1附近，那麽它就是well-conditioned的，如果遠大於1，那麽它就是 ill-conditioned 的。

　　總結：L2範數不但可以防止過擬合，還可以讓我們的優化求解變得穩定和快速。

L1和L2的差別，

1）下降速度：

我們知道，L1和L2都是規則化的方式，我們將權值參數以L1或者L2的方式放到代價函數裏面去。然後模型就會嘗試去最小化這些權值參數。而這個最小化就像一個下坡的過程，L1和L2的差別就在於這個“坡”不同，如下圖：L1就是按絕對值函數的“坡”下降的，而L2是按二次函數的“坡”下降。所以實際上在0附近，L1的下降速度比L2的下降速度要快，會非常快得降到0。

2）模型空間的限制：

實際上，對於L1和L2規則化的代價函數來說，我們可以寫成以下形式：

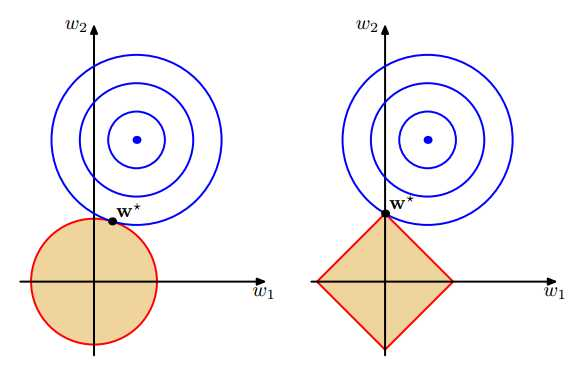
也就是說，我們將模型空間限制在w的一個L1-ball 中。為了便於可視化，我們考慮兩維的情況，在(w1, w2)平面上可以畫出目標函數的等高線，而約束條件則成為平面上半徑為C的一個 norm ball 。等高線與 norm ball 首次相交的地方就是最優解：

可以看到，L1-ball 與L2-ball 的不同就在於L1在和每個坐標軸相交的地方都有“角”出現，而目標函數的測地線除非位置擺得非常好，大部分時候都會在角的地方相交。註意到在角的位置就會產生稀疏性，例如圖中的相交點就有w1=0，而更高維的時候（想象一下三維的L1-ball 是什麽樣的？）除了角點以外，還有很多邊的輪廓也是既有很大的概率成為第一次相交的地方，又會產生稀疏性。

相比之下，L2-ball 就沒有這樣的性質，因為沒有角，所以第一次相交的地方出現在具有稀疏性的位置的概率就變得非常小了。這就從直觀上來解釋了為什麽L1-regularization 能產生稀疏性，而L2-regularization 不行的原因了。

總結：L1會趨向於產生少量的特征，而其他的特征都是0，而L2會選擇更多的特征，這些特征都會接近於0。Lasso在特征選擇時候非常有用，而Ridge就只是一種規則化而已。

有關上面配圖的解釋：

首先，我們要優化的是這個問題 。

其次， 和

這個優化問題是等價的，即對一個特定的 總存在一個 使得這兩個問題是等價的（這個是優化裏的知識）。

最後，下面這個圖表達的其實

這個優化問題，把 的解限制在黃色區域內，同時使得經驗損失盡可能小。

直觀來講：用梯度下降的方法，當w小於1的時候，L2正則項的懲罰效果越來越小，L1正則項懲罰效果依然很大，L1可以懲罰到0，而L2很難。

三、先驗知識角度理解L1和L2正則化與參數稀疏

作者：amnesia
鏈接：https://www.zhihu.com/question/37096933/answer/70668476
來源：知乎
著作權歸作者所有。商業轉載請聯系作者獲得授權，非商業轉載請註明出處。

首先你要知道L1範式和L2範式是怎麽來的,然後是為什麽要把L1或者L2正則項加到代價函數中去.
L1,L2範式來自於對數據的先驗知識.如果你認為,你現有的數據來自於高斯分布,那麽就應該在代價函數中加入數據先驗P(x),一般由於推導和計算方便會加入對數似然,也就是log(P(x)),然後再去優化,這樣最終的結果是,由於你的模型參數考慮了數據先驗,模型效果當然就更好.
哦對了,如果你去看看高斯分布的概率密度函數P(x),你會發現取對數後的log(P(x))就剩下一個平方項了,這就是L2範式的由來--高斯先驗.
同樣,如果你認為你的數據是稀疏的,不妨就認為它來自某種laplace分布.不知你是否見過laplace分布的概率密度函數,我貼出一張維基上的圖,
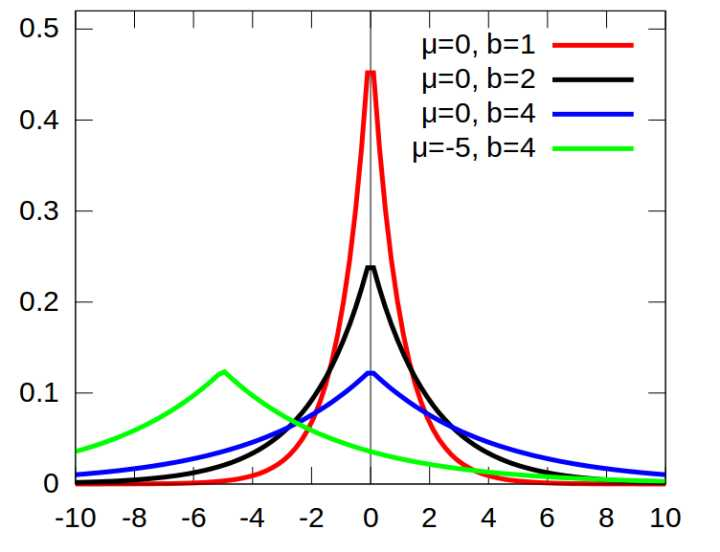
laplace分布是尖尖的分布,是不是很像一個pulse?從這張圖上,你應該就能看出,服從laplace分布的數據就是稀疏的了(只有很小的概率有值,大部分概率值都很小或為0).
那麽,加入了laplace先驗作為正則項的代價函數是什麽?
再看看laplace分布的概率密度函數(還是來自維基百科), 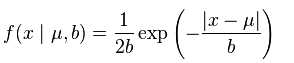看到沒,如果取對數,剩下的是一個一次項|x-u|,這就是L1範式.
所以用L1範式去正則,就假定了你的數據是laplace分布,是稀疏的.

四、數值計算角度理解L1和L2正則化與參數稀疏

作者：王赟 Maigo
鏈接：https://www.zhihu.com/question/37096933/answer/70426653
來源：知乎
著作權歸作者所有。商業轉載請聯系作者獲得授權，非商業轉載請註明出處。 假設費用函數 L 與某個參數 x 的關系如圖所示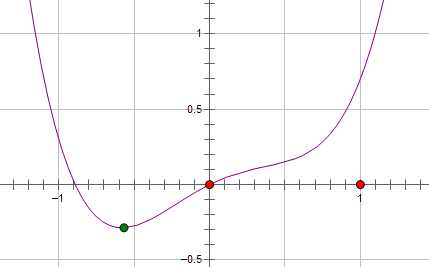： 則最優的 x 在綠點處，x 非零。

現在施加 L2 regularization，新的費用函數（）如圖中藍線所示：

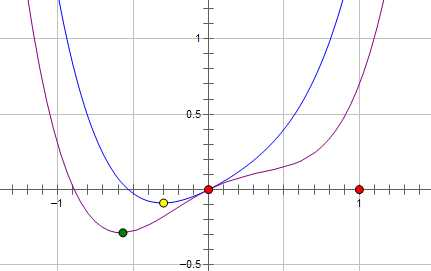最優的 x 在黃點處，x 的絕對值減小了，但依然非零。

而如果施加 L1 regularization，則新的費用函數（）如圖中粉線所示：

最優的 x 就變成了 0。這裏利用的就是絕對值函數的尖峰。

兩種 regularization 能不能把最優的 x 變成 0，取決於原先的費用函數在 0 點處的導數。
如果本來導數不為 0，那麽施加 L2 regularization 後導數依然不為 0，最優的 x 也不會變成 0。
而施加 L1 regularization 時，只要 regularization 項的系數 C 大於原先費用函數在 0 點處的導數的絕對值，x = 0 就會變成一個極小值點。

上面只分析了一個參數 x。事實上 L1 regularization 會使得許多參數的最優值變成 0，這樣模型就稀疏了。

『教程』L0、L1與L2範數_簡化理解