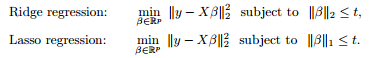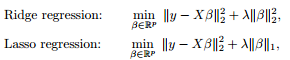關於L0,L1和L2範數的規則化
本文主要整理一下機器學習中的範數規則化學習的內容:
- 規則化
-什麼是規則化
-為什麼要規則化
-規則化的理解
-怎麼規則化
-規則化的作用 - 範數
-L0範數和L1範數
-L2範數
-L1範數和L2範數 - 補充
-condition number
-微博、知乎部分討論 - 參考附錄
規則化
什麼是規則化?
回顧一下機器學習演算法的3個要點:1.根據資料找合適的模型;2.定義損失以評估模型;3.設計求解優化的方法。
再回顧一下監督學習:規則化引數(防止模型過分擬合訓練資料)的同時最小化誤差(模型擬合訓練資料的偏差)。
Regularization, in mathematics and statistics and particularly in the fields of machine learning and inverse problems, refers to a process of introducing additional information in order to solve an ill-posed problem or to prevent overfitting. —— from wikipedia
Regularization是引入額外的資訊來解決ill-posed問題或者防止overfitting的過程。
規則化的表現形式:
第一項是衡量模型對樣本的預測與真實的誤差(二者越接近越好),最小化誤差指該部分。
第二項是對引數w的規則化函式Ω(w)約束模型(使模型簡單)。最小化模型測試誤差指該部分。
為什麼要規則化?
為了解決ill-posed問題或者防止overfitting,期望獲得一個能夠很好地解釋資料而且simple的模型,或者從統計角度來說,是找一個減少過度擬合的估計方法。
一般從線性迴歸問題也稱最小二乘問題(Least Squares Problem, LSP)和邏輯迴歸問題(Logistic Regression Problem, LRP)引入。前者想象預測的變數是數字,後者預測的變數是“是/否”的這種分類答案。這兩個問題中會出現下面的情況導致overfitting:
- When the number of observations or training examples m is not large enough compared to the number of feature variables n, over-fitting may occur. 樣本數量m選不如特徵維度n大
- Tends to occur when large weights are found in x. 待預測的向量x的有過大的權重,也就是擬合函式的係數過大【考慮太過全面,把noise 或者 error in the data都考慮進去了,過分擬合。這樣導致擬合函式波動大。同一量級上考慮,係數小曲線偏平滑,係數大,曲線偏陡峭】
針對1.解決方法是:
- 減少特徵數量
- 可以人工選擇重要的特徵變數以減少特徵數。
- 自動的,特徵選擇(Feature Selection) -> 稀疏性 -> 正則化
-增加樣本數量
針對2.解決方法是:
- 正則化
當然還有其他的方法,本文不介紹了。eg.cross-validation, early stopping, pruning, Bayesian priors on parameters or model comparison
規則化的理解
讓模型簡單,意味著要採取措施降低模型複雜度(過多引數導致模型複雜–稀疏 is ok),使用規則項來約束模型(約束了待學習的模型引數w,也就變相約束了模型)的特性。
還有幾種種理解角度:
角度一
經驗風險=平均損失函式 ,結構風險=損失函式+正則化項(懲罰項)
正則化是結構風險最小化的策略。正則化項一般是模型複雜度的單調遞增函式,模型越複雜,正則化值就越大。比如,模型引數向量的範數。角度二
正則化項的引入其實是利用了先驗知識,體現了人對問題的解的認知程度或者對解的估計。這樣就可以將人對該問題的理解和需求(先驗知識)融入到模型的學習當中,對模型引數設定先驗,強行地讓學習到的模型具有人想要的特性,例如稀疏、低秩、平滑等等。(正則與稀疏、低秩和平滑的關係)
L1正則是laplace先驗,l2是高斯先驗,分別由引數sigma確定。角度三
附錄的Sparsity and the Lasso
最小二乘問題中,ranx(A)<樣本數量。對要解決的問題加限制條件(角度二中的先驗)–>[subject to]
影象表示出來是這樣的:
利用對偶,KKT等轉化成這樣:為什麼要凸的,這就用著了。
本質上都差不多,切入點不同,就可以從不同方面理解了。
怎麼規則化?
前面提到,正則化項一般是模型複雜度的單調遞增函式,模型越複雜,正則化值就越大(為了給予複雜模型以懲罰,因為優化的時候要最小化函式,想要得到simple模型,越複雜,懲罰越大),並且優化過程還想得到稀疏的引數。(看怎麼理解稀疏了,L1引數大多為0,L2引數大多接近0)。下面介紹的是用向量範數的形式來規則化,看範數那一節。
為什麼引數要稀疏呢?——特徵選擇;問題的可解釋性
1. 特徵選擇:large-scale 可能大部分特徵是對於最終的輸出y是無影響的或者影響很小的。訓練時最小化目標函式,如果考慮這些特徵會得到更小的誤差,但是會對新樣本的預測結果產生影響。Lasso regularization的引入是為了完成特徵自動選擇,它會在優化過程中主動去學習去掉這些沒有用的特徵,把特徵對應的權重置為0。【L1】
2. 可解釋性:例如一回歸問題,假設迴歸模型為:y=w1*x1+w2*x2+…+w1000*x1000+b。通過學習,如果最後學習到的w*,只有很少的非零元素,大部分w*為0或接近於0,例如只有5個非零的wi,那可以認為y只受這5個xi(因素)的影響,更有利於人們對問題的認識和分析,抓住影響問題的主要方面(因素)更符合認知習慣。【L2】
【正則與平滑】實際上,這些引數值越小,通常對應于越光滑的函式,也就是更加簡單的函式。
【正則與稀疏】為什麼正則化會使引數稀疏呢?
規則化的作用?
- 防止過擬合(平衡了偏差與方差,擬合能力與泛化能力,結構風險和經驗風險);
- 正則化導致的稀疏性是有益的:特徵選擇以及把人對於問題的認知作為先驗引入優化過程中;
- 降低condition number,處理因其過大導致逆矩陣不好求的情況;
範數
L0範數和L1範數
L0範數是指向量中非0的元素的個數。
L1範數是指向量中各個元素絕對值之和,也稱Lasso regularization
如果用L0範數來規則化一個引數矩陣W的話,就是希望W的大部分元素都是0,也就是讓引數W是稀疏的。L0應該不算是norm。像L1,L2等可以轉換到convex或者本身就是convex的這種算norm。(能用來優化)
為什麼L1範數會使權值稀疏?
見L1範數和L2範數部分。
L2範數
指向量各元素的平方和再求平方根。讓L2範數的規則項最小,可以使得W的每個元素都很小,都接近於0,但與L1範數不同,它不會讓它等於0,而是接近於0。
L2範數好處
1.學習理論角度——L2範數可以防止過擬合,提升模型的泛化能力
2.優化計算角度——L2範數有助於處理 矩陣 condition number不好的情況下矩陣求逆很困難的問題
為什麼L2範數有助於處理矩陣condition number不好的情況下矩陣求逆很困難的問題?
以最小二乘問題LSP為例,新增正則項(add “preference” for certain parameter values)之後的cost function J :
用同樣的方法,求得新的解的表示式為
此時,該問題是well-posed,加入了L2正則後,改善了
L1範數和L2範數
Unlike the L2-regularization which restricts large values, the L1-regularization term penalizes all factors equally, which can create sparse answers.
參考附錄9
- example 1

解釋一下,考慮向量
L2範數結果,考慮減小
L1範數結果,不論擾動給x1還是x2,前後的reduction都是
用L2範數懲罰模型,懲罰程序中,不太可能有任何元素被置為0。主要看值小的那一項(給x2添擾動,值小的靠近0,看看他的變化情況),
L1範數懲罰可以使稀疏;L2懲罰過程中,元素朝著0移動的這種reduction越來越小,意味著移動速度越來越慢,一定程度上阻礙了稀疏性。可以根據範數的影象,看導數。
- example 2
考慮含有引數
本文主要整理一下機器學習中的範數規則化學習的內容:
規則化
-什麼是規則化
-為什麼要規則化
-規則化的理解
-怎麼規則化
-規則化的作用
範數
-L0範數和L1範數
-L2範數
-L1範數和L2範數
補充
-condition numbe
如果是Square loss,那就是最小二乘了;
如果是Hinge Loss,那就是著名的SVM了;
如果是exp-Loss,那就是牛逼的 Boosting了;
如果是log-Loss,那就是Logistic Regression了;
L0範數是指向量中非0的元素的 [0 證明 基本上 復雜度 所有 img 方法 風險 機器學習 機器學習中的範數規則化之(一)L0、L1與L2範數
[email protected]/* */
http://blog.csdn.net/zouxy09
轉自:http://blog.csdn.n spa http span get font lan pan href -s http://blog.csdn.net/zouxy09/article/details/24971995【轉】範數規則化L0、L1與L2範數 實驗 方程 為什麽 over 大數據 來講 退回 數據庫 解釋 今天看到一篇講機器學習範數規則化的文章,講得特別好,記錄學習一下。原博客地址(http://blog.csdn.net/zouxy09)。
今天我們聊聊機器學習中出現的非常頻繁的問題:過擬合與規則化。我
今天我們聊聊機器學習中出現的非常頻繁的問題:過擬合與規則化。我們先簡單的來理解下常用的L0、L1、L2和核範數規則化。最後聊下規則化項引數的選擇問題。這裡因為篇幅比較龐大,為了不嚇到大家,我將這個五個部分分成兩篇博文。知識有限,以下都是我一些淺顯的
今天我們聊聊機器學習中出現的非常頻繁的問題:過擬合與規則化。我們先簡單的來理解下常用的L0、L1、L2和核範數規則化。最後聊下規則化項引數的選擇問題。這裡因為篇幅比較龐大,為了不嚇到大家,我將這個五個部分分成兩篇博文。知識有限,以下都是我一些淺顯的看法,如果理解存在錯誤
監督機器學習問題無非就是“minimizeyour error while regularizing your parameters”,也就是在規則化引數的同時最小化誤差。最小化誤差是為了讓我們的模型擬合我們的訓練資料,而規則化引數是防止我們的模型過分擬合我們的訓練資料。多麼
機器學習中的範數規則化之(一)L0、L1與L2範數
今天我們聊聊機器學習中出現的非常頻繁的問題:過擬合與規則化。我們先簡單的來理解下常用的L0、L1、L2和核範數規則化。最後聊下規則化項引數的選擇問題。這裡因為篇幅比較龐大,為了不嚇到大家,我將這個五
今天我們聊聊機器學習中出現的非常頻繁的問題:過擬合與規則化。我們先簡單的來理解下常用的L0、L1、L2和核範數規則化。最後聊下規則化項引數的選擇問題。這裡因為篇幅比較龐大,為了不嚇到大家,我將這個五個部分分成兩篇博文。知識有限,以下都是我一些淺顯的看法,如果理解存在錯誤,希 線性 實驗 tab 下一個 約束 特征 方式 等於 b2c
『教程』L0、L1與L2範數
一、L0範數、L1範數、參數稀疏
L0範數是指向量中非0的元素的個數。如果我們用L0範數來規則化一個參數矩陣W的話,就是希望W的大部分元素都是0,換句話說,讓參數W
在深度學習中,監督類學習問題其實就是在規則化引數同時最小化誤差。最小化誤差目的是讓模型擬合訓練資料,而規則化引數的目的是防止模型過分擬合訓練資料。
引數太多,會導致模型複雜度上升,容易過擬合,也就是訓練誤差小,測試誤差大。因此,我們需要保證模型足夠簡單,並在此基礎上訓練誤差小,這樣訓練得到的引數 OK,回到問題本身。我們選擇引數λ的目標是什麼?我們希望模型的訓練誤差和泛化能力都很強。這時候,你有可能還反映過來,這不是說我們的泛化效能是我們的引數λ的函式嗎?那我們為什麼按優化那一套,選擇能最大化泛化效能的λ呢?Oh,sorry to tell you that,因為泛化效能並不是λ的簡單的函式!它具有很
1 L0範數
L0範數表示向量中非0元素的個數,即希望資料集中的大部分元素都是0(即希望資料集是稀疏的),
所以可以用於ML中做稀疏編碼,特徵選擇,即通過L0範數來尋找最少最優的稀疏特徵項。
但不幸的是,L0範數的最優化問題是一個NP hard問題,而且理論上有證明
正則化(Regularization)
機器學習中幾乎都可以看到損失函式後面會新增一個額外項,常用的額外項一般有兩種,一般英文稱作ℓ1-norm和ℓ2-norm,中文稱作L1正則化和L2正則化,或者L1範數和L2範數。
L1正則化和L2正則化可以看做是損失 知識 tin gis res 學習 sdn 一個 們的 ssi 監督機器學習問題無非就是再規則化參數的同時最小化誤差。
*最小化誤差是為了讓我們的模型擬合我們的訓練數據,而規則化參數是防止我們的模型過分擬合我們的訓練數據
規則化參數的作用:
*使得模型簡單,且具有好的
正則化和範數規則化
文章安排:文章先介紹了正則化的定義,然後介紹其在機器學習中的規則化應用L0、L1、L2規則化範數和核範數規則化,最後介紹規則化項引數的選擇問題。
正則化(regularization)來源於線性代數理論中的不適定問題,求解不適定問題的普遍方法是:用一族與
先看上面l21範數的定義,注意原始矩陣是n行t列的,根號下平方是對列求和,也就是說是在同一行中進行操作的,根號部分就相當於一個l2範數,由此可以看出l21範數實則為矩陣X每一行的l2範數之和。
在矩陣稀疏表示模型中,把它作為正則化項有什麼作用呢?前面說到它是每一行的l2範數之和,在最小 作為一個非理工科的經管學生,在數學基礎有限的情況的,理解難免不足。文章多有copy。
參考部落格:
https://blog.csdn.net/zouxy09/article/details/24971995
1.前言
為什麼探討L0,L1,L2範數,機器學習中出現的非 OK,回到問題本身。我們選擇引數λ的目標是什麼?我們希望模型的訓練誤差和泛化能力都很強。這時候,你有可能還反映過來,這不是說我們的泛化效能是我們的引數λ的函式嗎?那我們為什麼按優化那一套,選擇能最大化泛化效能的λ呢?Oh,sorry to tell you that,因為泛化效能並不是λ的簡單的函式!它具有很 相關推薦
關於L0,L1和L2範數的規則化
常用loss以及L0,L1以及L2範數
機器學習中的範數規則化之(一)L0、L1與L2範數
【轉】範數規則化L0、L1與L2範數
機器學習中的範數規則化之L0、L1與L2範數
機器學習中的範數規則化之 L0、L1與L2範數
轉:機器學習中的範數規則化之(一)L0、L1與L2範數
轉載:機器學習中的範數規則化之(一)L0、L1與L2範數
機器學習中的範數規則化之 L0、L1與L2範數
機器學習中的範數規則化之(一)L0、L1與L2範數、核範數與規則項引數選擇
『教程』L0、L1與L2範數_簡化理解
深度學習——L0、L1及L2範數
L0、L1、L2範數與核範數(二)
L0、L1、L2範數學習筆記
L1範數和L2範數的區別
L1和L2範式
機器學習中的正則化和範數規則化
機器學習中的範數規則化之L21範數
範數規則化
【機器學習】範數規則化之(二)核範數與規則項引數選擇