矩陣、歐拉角、軸-角對、四元數隨筆
一、矩陣
在 3D 遊戲中,可以使用矩陣來表示一個物體的旋轉。
1) 優點:
個人認為,理解起來最為直觀。
像現成的DXSDK庫中也提供了十分完善的相關接口
一個矩陣即可表示多種變換的組合
2) 缺點:
每次計算都會產生誤差,因此,需要經常規範化。
耗的內存較多些。
二、歐拉角
歐拉角指的是:以世界坐標系為參考坐標系(一定記住是世界坐標系),使用x,y,z三個值來分別表示繞(世界的)x軸、y軸、z軸旋轉的角度量值。其取值是在[0, 360]間。一般用roll, pitch, yaw來表示這些分量的旋轉值。因為是以世界坐標系為參考坐標系,因此每一次的旋轉都不會影響到後續的旋轉轉軸。即:它無法表示任意軸的旋轉。
1) 優點:
理解起來很直觀。
2) 缺點:
會有萬向鎖問題。
三、軸-角對
其實軸-角對與歐拉角(個人認為)是有一定的關系的。因為歐拉角說的是分別(註意:是分別)繞(以世界坐標系為參考坐標系的)三個軸旋轉一定的角度。其實這三次的旋轉可以最終轉換到一次變換。即:最終可表示為:繞某一旋轉軸旋轉一定角度的變換。(意思就是說:那三次變換我們最終可以計算出旋轉軸以及繞該旋轉軸旋轉的角度量)。
1) 缺點:
軸-角對表示法:插值不平滑,可能會有跳躍。(文檔上說,歐拉角同樣存在這個問題)
2) 優點:
可解決歐拉角的萬向鎖問題。
四、四元數
四元數定義:q = w + xi + yj + zk
註意:
1) 四元數可以歸一化,並且只有歸一化的四元數才用來描述旋轉
2) 四元數與軸-角對很像。因為四元數描述的也是一個旋轉軸與一個繞著該旋轉軸旋轉的量值(即:角度或弧度)。但四元數與軸-角對不等價。它們的關系如下:
假如:軸-角對的值如下:
軸為:n
角為:theta
則,對應的四元數中的w、x、y、z的值分別為:
w = cos(theta / 2)
x = nx * sin(theta / 2) // nx 是軸 n 的 x 分量
y = ny * sin(theta / 2) // ny 是軸 n 的 y 分量
z = nz * sin(theta / 2) // nz 是軸 n 的 z 分量
3) 四元數的乘法意義:
Q = Q1 * Q2表示的是:Q先做Q2的旋轉,再做Q1的旋轉的結果,而且多個四元數的旋轉也是要以合並的。
4) 四元數做一次乘法需要16次乘法和加法,而3x3矩陣需要27次。所以有多次旋轉操作時,使用四元數計算效率更高些。
5) 四元數的插值過度平滑。最常用的是線性插值。
關於軸-角對的理解可參照Alex四元數解算的程序(角度+每軸的分量)。
在3D圖形學中,最常用的旋轉表示方法便是四元數和歐拉角,比起矩陣來具有節省存儲空間和方便插值的優點。本文主要歸納了兩種表達方式的轉換,計算公式采用3D笛卡爾坐標系:
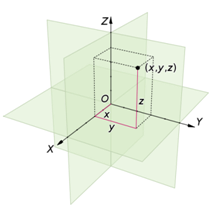
圖1 3D Cartesian coordinate System (from wikipedia)
定義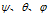 分別為繞Z軸、Y軸、X軸的旋轉角度,如果用Tait-Bryan angle表示,分別為Yaw、Pitch、Roll。
分別為繞Z軸、Y軸、X軸的旋轉角度,如果用Tait-Bryan angle表示,分別為Yaw、Pitch、Roll。
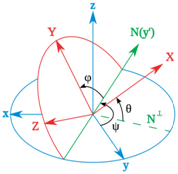
圖2 Tait-Bryan angles (from wikipedia)
一、四元數的定義
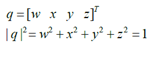
通過旋轉軸和繞該軸旋轉的角度可以構造一個四元數 :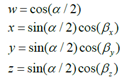
其中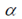 是繞旋轉軸旋轉的角度,
是繞旋轉軸旋轉的角度,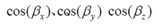 為旋轉軸在x,y,z方向的分量(由此確定了旋轉軸)。
為旋轉軸在x,y,z方向的分量(由此確定了旋轉軸)。
二、歐拉角到四元數的轉換
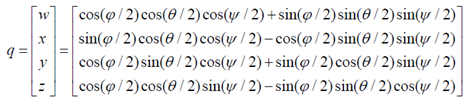
三、四元數到歐拉角的轉換

arctan和arcsin的結果是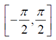 ,這並不能覆蓋所有朝向(對於
,這並不能覆蓋所有朝向(對於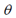 角
角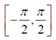 的取值範圍已經滿足),因此需要用atan2來代替arctan。
的取值範圍已經滿足),因此需要用atan2來代替arctan。
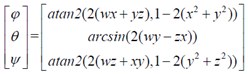
四、在其他坐標系下使用
在其他坐標系下,需根據坐標軸的定義,調整一下以上公式。如在Direct3D中,笛卡爾坐標系的X軸變為Z軸,Y軸變為X軸,Z軸變為Y軸(無需考慮方向)。
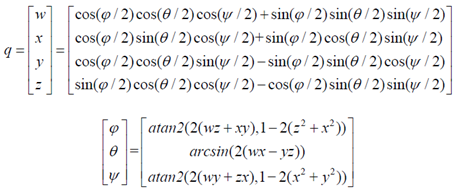
矩陣、歐拉角、軸-角對、四元數隨筆
