線性時不變系統的定義

線性時不變系統（LTI）是離散時間系統中特別重要的一種系統，該系統包含線性以及時不變性，用卷積來表征。

前面有講過序列$x[n]$可以表示成幅度加權的延遲單位樣本序列的和的形式

$x[n] = \displaystyle{ \sum_{k=-\infty}^{\infty}x[k]\delta[n-k] }$

因此離散時間系統可以表示成如下形式

$y[n] = T\left\{ \displaystyle{ \sum_{k=-\infty}^{\infty}x[k]\delta[n-k] } \right\}$

如果系統是線性的，那麽由於式子中的變量為$n$，根據疊加原理，$\displaystyle{ \sum_{k=-\infty}^{\infty}x[k] }$可以移出$T$

$y[n] = \displaystyle{ \sum_{k=-\infty}^{\infty}x[k]T\{ \delta[n-k] \} }$

我們令$h_k[n] = T\{\delta[n-k]\}$，$h_k[n]$就是該線性系統對輸入為$\delta[n-k]$所產生的輸出，也就是系統對位於$n=k$處脈沖的響應，被稱為脈沖響應（impulse response）。

如果系統是時不變的，這意味著如果$h[n]$是系統對$\delta[n]$的響應，那麽$h[n-k]$就是系統對$\delta[n-k]$的響應，此時可以得到

$y[n] = \displaystyle{ \sum_{k=-\infty}^{\infty}x[k]h[n-k] }$

上面的式子表明，對於一個線性時不變系統，如果我們知道其的全部輸入$x[n]$以及該系統的脈沖響應$h[n]$，則能得到其全部輸出$y[n]$。該式子一般被稱為卷積和（convolution sum），並用下述操作符號表示

$y[n] = x[n]*h[n]$

LTI系統的兩種解釋/計算方式

如上一小節所述，線性時不變系統對應的算式為

$y[n] = \displaystyle{ \sum_{k=-\infty}^{\infty}x[k]h[n-k] }$

單獨分析每一個輸入脈沖

LTI系統可以理解為：對於序列$x[n]$中的某一項脈沖$x[k_0]$，其在經過LTI系統後得到的脈沖響應為$x[k_0]h[n-k_0]$，把序列$x[n]$的所有脈沖的脈沖響應線性相加就得到最終輸出$y[n]$。

假設有一個LTI系統，其輸入序列$x[n]$、系統脈沖響應$h[n]$如下

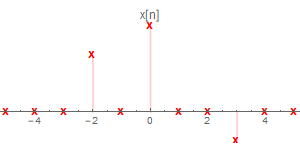
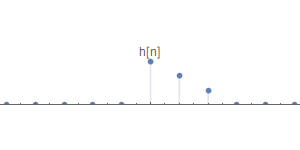
可以看到$x[n]$有三個脈沖$x_{-2}[n],x_{0}[n],x_{3}[n]$，我們把這三個脈沖單獨取出來，分別計算它們經過LTI系統後的的脈沖響應。

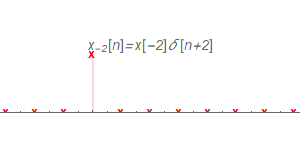
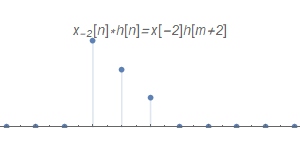
把$x_{-2}[n]$看作加權$x[-2]$與$\delta[n+2]$的乘積，按照LTI系統的時不變性質，$\delta[n+2]$的脈沖響應就是$h[n+2]$；又因為LTI系統的線性性質，可以得到$x_{-2}[n]$的脈沖響應為$x[-2]h[n+2]$。同理，剩下的脈沖響應如下

$x_{0}[n]$

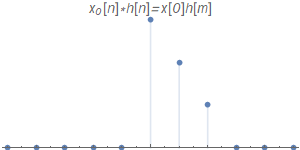
$x_{3}[n]$

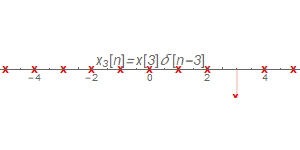
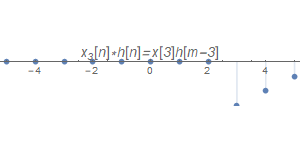
最後由於LTI系統具有線性性質，因此把所有的脈沖響應結果線性相加，即可得到$x[n]$經過系統後的輸出$y[n]$

單獨分析每一個輸出脈沖

$y[n]$是系統的輸出序列，對於某一時間點$n_0$的輸出脈沖$y[n_0]$，我們可以通過卷積分析該輸出脈沖如何通過計算得到，按照這種計算方法對所有時間點的輸出脈沖進行計算，就能得到整個輸出序列$y[n]$。

我們首先取某時間點$n_0$，其輸出脈沖為

$y[n_0] = \displaystyle{ \sum_{k=-\infty}^{\infty}x[k]h[n_0-k] }$

此時，式子當中的$n_0$為常量，$k$為變量，我們接下來觀察$h[n_0-k]$是通過$h[k]$做何種變化得到的。

1. 令$h_1[k]=h[-k]$，即$h[k]$對$k=0$軸進行對稱反轉即可得到$h_1[k]$
2. 令$h_2[k]=h_1[k-n_0]$，即$h_1[k]$向右移動$n_0$個單位即可得到$h_2[k]$

$h_2[k] = h_1[k-n_0]=h[-(k-n_0)]=h[n_0-k]$

在知道輸入$x[k]$的情況下，現在我們又得到了$h[n_0-k]$，如此一來就能通過上述式子的乘積求和計算得到$y[n_0]$。通過改變$n_0$，就能得到輸出序列$y[n]$。

假設有一LTI系統的脈沖響應$h[n]$及其輸入$x[n]$如下

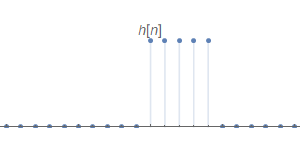
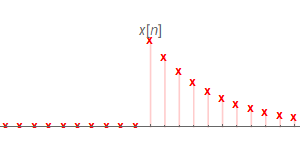
當$n_0<0$的時候，$h[n_0-k]$與$x[k]$並沒有相交，因此$y[n_0]=0$

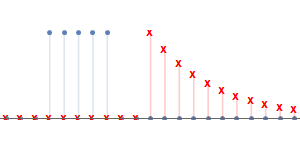
從$n_0=0$開始，$h[n_0-k]$與$x[k]$部分相交，直到$n_0=4$開始完全相交，因此在這段時間內計算得到的$y[n_0]$呈上升趨勢

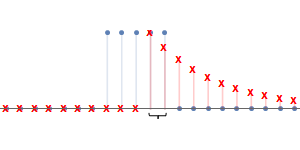
在$n_0=4$時有最大值$y[4]$，然後$y[n_0]$呈下降趨勢

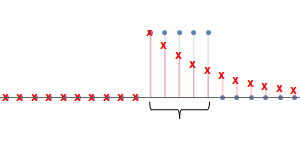
最終得到的$y[n]$如下

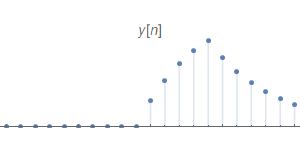
線性時不變系統的性質

交換律、分配律、結合律

LTI系統由離散時間卷積來定義，而卷積滿足交換律、分配律、結合律。

交換律推導：

$\begin{align*}
y[n] &=x[n]*h[n] \\
&=\sum_{m=-\infty}^{\infty}x[n-m]h[m] \\
&=\sum_{p=-\infty}^{\infty}x[p]h[n-p] \quad letting\ p=n-m \\
&=\sum_{p=-\infty}^{\infty}h[n-p]x[p] \\
&=h[n]*x[n]
\end{align*}$

分配律推導：

$\begin{align*}
y[n] &=x[n]*h[n] \\
&=x[n]*(h_1[n]+h_2[n]) \\
&=\sum_{m=-\infty}^{\infty}x[n-m](h_1[m]+h_2[m]) \\
&=\sum_{m=-\infty}^{\infty}x[n-m]h_1[m]+\sum_{m=-\infty}^{\infty}x[n-m]h_2[m] \\
&=x[n]*h_1[n]+x[n]*h_2[n]
\end{align*}$

結合律推導：

$\begin{align*}
y[n] &=(x[n]*h_1[n])*h_2[n] \\
&=z[n]*h_2[n] \\
&=\sum_{m=-\infty}^{\infty}z[n-m]h_2[m] \\
&=\sum_{p=-\infty}^{\infty}z[p]h_2[n-p] \quad letting\ p=n-m\\
&=\sum_{p=-\infty}^{\infty}\left ( \sum_{i=-\infty}^{\infty}x[p-i]h_1[i] \right )h_2[n-p] \\
&=\sum_{p=-\infty}^{\infty}\left ( \sum_{q=-\infty}^{\infty}x[q]h_1[p-q] \right )h_2[n-p] \quad letting\ q=p-i\\
&=\sum_{q=-\infty}^{\infty}x[q]\left ( \sum_{p=-\infty}^{\infty}h_1[p-q]h_2[n-p] \right ) \\
&=\sum_{q=-\infty}^{\infty}x[q]\left ( \sum_{m=-\infty}^{\infty}h_1[n-q-m]h_2[m] \right ) \\
&=\sum_{k=-\infty}^{\infty}x[n-k]\left ( \sum_{m=-\infty}^{\infty}h_1[k-m]h_2[m] \right ) \quad letting\ k=n-q \\
&=x[n]*(h_1[n]*h_2[n])
\end{align*}$

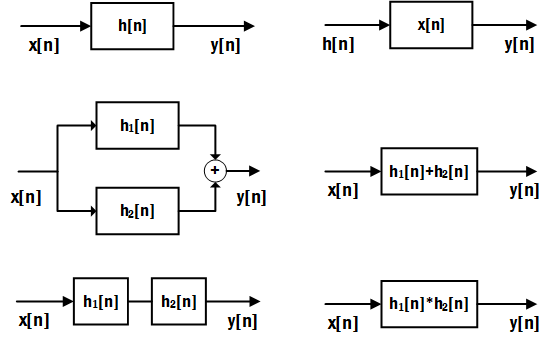
因此LTI系統有如下性質：

• 一個LTI系統在輸入為$x[n]$和單位脈沖響應為$h[n]$，與輸入為$h[n]$和單位脈沖響應為$x[n]$將得到相同的輸出。
• 一個LTI系統如果由並聯的兩個部分組成，其單位脈沖響應分別為$h_1[n],h_2[n]$，那麽整個系統的單位脈沖響應等價於$h[n]=h_1[n]+h_2[n]$。
• 一個LTI系統如果由級聯的兩個部分組成，其單位脈沖響應分別為$h_1[n],h_2[n]$，那麽整個系統的單位脈沖響應等價於$h[n]=h_1[n]*h_2[n]$。

穩定性

認為一個穩定系統就是對每個有界的輸入均產生一個有界的輸出。當單位脈沖響應是絕對可加時，LTI系統才是穩定的，即

$B_h=\displaystyle{ \sum_{k=-\infty}^{\infty}|h[k]|<\infty }$

證明：

$\displaystyle{ |y[n]|=\left | \sum_{k=-\infty}^{\infty}h[k]x[n-k] \right |\leqslant\sum_{k=-\infty}^{\infty}|h[k]||x[n-k]| }$

如果$x[n]$是有界的，則存在一個足夠大的數$B_x$，使得

$|x[n]|\leqslant B_x$

用$B_x$替換$|x[n-k]|$可以得到一個更大的數值，即

$|y[n]|\leqslant B_xB_h$

因此，當單位脈沖響應是絕對可加時，LTI系統是穩定的。

因果性

因果系統就是其輸出$y[n_0]$僅僅與$n\leqslant n_0$時的輸入樣本$x[n]$有關的系統，如果一個LTI系統是因果系統，則該系統應滿足

$h[n]=0, \quad n<0$

證明：

設某時刻$n_1$的輸出為$y[n_1]$，有

$\begin{align*}
y[n_1] &= \sum_{k=-\infty}^{\infty}x[k]h[n_1-k] \\
&=\sum_{k=-\infty}^{n_1}x[k]h[n_1-k]+\sum_{k=n_1+1}^{\infty}x[k]h[n_1-k]
\end{align*}$

因為是因果系統，即$y[n_1]$與輸入序列$x[k]$的$k>n_1$部分無關，即

$\displaystyle{ \sum_{k=n_1+1}^{\infty}x[k]h[n_1-k] =0}$

令$m=n_1-k,k=n_1-m$，代入上式，得到

$\displaystyle{ \sum_{m=-\infty}^{-1}x[n_1-m]h[m]=0 }$

其中$x[m]$為可變的輸入序列，要使上式成立，則需要

$h[m]=0,\quad m<0$

級聯系統的某些應用

LTI系統用卷積來表征，並且從前一小節我們得知級聯系統由離散時間卷積來表征。兩個序列之間的卷積運算會帶來很多涉及系統問題的簡化。

一個很常用的應用就是將一個移位樣本序列與任何$x[n]$進行卷積，其結果只是將$x[n]$做相同的移位：

$x[n] * \delta[n-n_d] = \delta[n-n_d] * x[n] = x[n-n_d]$

這種移位的應用在LTI系統互聯與分析中也常常用到，如一個前向差分與一個理想延遲（延遲一個樣本）級聯就能得到一個後向差分：

$\begin{align*}
h[n] &=(\delta[n+1]-\delta[n])*\delta[n-1] \\
&=\delta[n-1]*(\delta[n+1]-\delta[n]) \\
&=\delta[n]-\delta[n-1]
\end{align*}$

另外，級聯系統引入了逆系統（inverse system）的概念，

$h[n] * h_i[n] = h_i[n] * h[n] = \delta[n]$

如果兩個系統級聯後得到的是$\delta[n]$，則這兩個系統互為逆系統。

[離散時間信號處理學習筆記] 2. 線性時不變系統