離散數學學習筆記-2-群 子群
阿新 • • 發佈:2018-12-21
群 環 域
群的第一定義
非空封閉結合律 有一有逆
滿足前三個叫做半群,

第二定義的推導


第二定義:

推導第一定義:推導過程
首先證明 a和a-1滿足交換律,這樣就可以證明 左單位就是右單位

群的分類


叫做阿貝爾群

性質: 單位元和逆元唯一性


階數的定義 : 這個就要注意了,群的運算不確定,這個次方表示連續運算m次,
並且是最小的正整數
運算可能是加法噢
不同元的階數可能不同(但是有規律)

有逆元代表滿足消去律------那麼有逆元是不是就沒有零因子了
那麼三者就是等價的咯(前提是有限群)


有限群的另一個定義就是消去律 和 有解是等價,有解不就要有逆了(無限群大部分元素沒有逆)

群的同態==========這裡只說同態,預設是滿同態就行了


上面證明可以得到;

變換

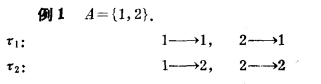
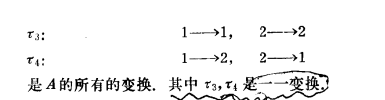
重點來了: (複合運算) 注意這個集合說的是 所有變換 而不是所有一一變換

請注意集合是所有變換,單位元是 恆等變換


===========很顯然一一對映就可以解決了
證明來了—已知滿射,證明單射

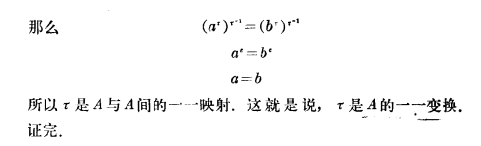
變換群登場-----元素 A集合的一一對映




重點來了!!! 怎麼看怎麼像輪換
也就是同構的那個變換群是 A集合的所有一一變換的一部分!

置換群

這個就驗證之前的說法 全體置換是對稱群,那麼上面同構的只是子群
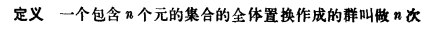

表示方法
把第一行看成自變數 第二行就是因變數



迴圈置換

分解




迴圈群

也就是一個迴圈群肯定和一個加群同構


子群
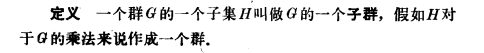


合併一下條件 關鍵是找出單位元(很多證明都是利用單位元搞事情)

子群條件


生成子群

