前端學數據結構之集合
前面的話
本文將詳細介紹集合,這是一種不允許值重復的順序數據結構
數據結構
集合是由一組無序且唯一(即不能重復)的項組成的。這個數據結構使用了與有限集合相同的數學概念,但應用在計算機科學的數據結構中。
在深入學習集合的計算機科學實現之前,我們先看看它的數學概念。在數學中,集合是一組不同的對象(的集)。比如說,一個由大於或等於0的整數組成的自然數集合:N={0,1,2,3,4,5,6,…}。集合中的對象列表用“{}”(大括號)包圍。
還有一個概念叫空集。空集就是不包含任何元素的集合。比如24和29之間的素數集合。由於24和29之間沒有素數(除了1和自身,沒有其他正因數的大於1的自然數),這個集合就是空集。空集用“{}”表示
也可以把集合想象成一個既沒有重復元素,也沒有順序概念的數組。在數學中,集合也有並集、交集、差集等基本操作。下面將介紹這些操作
創建集合
下面要實現的類就是以ECMAScript6中Set類的實現為基礎的。
以下是Set類的骨架:
function Set() { var items = {}; }
有一個非常重要的細節,我們使用對象而不是數組來表示集合(items)。但也可以用數組實現。 同時,JavaScript的對象不允許一個鍵指向兩個不同的屬性,也保證了集合裏的元素都是唯一的
接下來,需要聲明一些集合可用的方法(我們會嘗試模擬與ECMAScript 6實現相同的Set類)
add(value):向集合添加一個新的項。
remove(value):從集合移除一個值。
has(value):如果值在集合中,返回true,否則返回false。
clear():移除集合中的所有項。
size():返回集合所包含元素的數量。與數組的length屬性類似。
values():返回一個包含集合中所有值的數組。
【has】
首先要實現的是has(value)方法。這是因為它會被add、remove等其他方法調用。
既然我們使用對象來存儲集合的值,就可以用JavaScript的in操作符來驗證給定的值是否是items對象的屬性
下面看看它的實現:
this.has = function(value){ return value in items; };
但這個方法還有更好的實現方式,所有JavaScript對象都有hasOwnProperty方法。這個方法返回一個表明對象是否具有特定屬性的布爾值。代碼如下:
this.has = function(value){ return items.hasOwnProperty(value); };
【add】
接下來要實現add方法:
this.add = function(value){ if (!this.has(value)){ items[value] = value; //{1} return true; } return false; };
對於給定的value,可以檢查它是否存在於集合中。如果不存在,就把value添加到集合中(行{1}),返回true,表示添加了這個值。如果集合中已經有這個值,就返回false,表示沒有添加它。
[註意]添加一個值的時候,把它同時作為鍵和值保存,因為這樣有利於查找這個值
【remove】
在remove方法中,我們會驗證給定的value是否存在於集合中。如果存在,就從集合中移除value(行{2}),返回true,表示值被移除;否則返回false。
下面來實現remove方法:
this.remove = function(value){ if (this.has(value)){ delete items[value]; //{2} return true; } return false; };
既然用對象來存儲集合的items對象,就可以簡單地使用delete操作符從items對象中移除屬性(行{2})
使用Set類的示例代碼如下:
var set = new Set(); set.add(1); set.add(2);
在執行以上代碼之後,在控制臺(console.log)輸出items 變量,Chrome就會輸出如下內容:
Object {1: 1, 2: 2}
可以看到,這是一個有兩個屬性的對象。屬性名就是添加到集合的值,同時它也是屬性值
【clear】
如果想移除集合中的所有值,可以用clear方法:
要重置items對象,需要做的只是把一個空對象重新賦值給它(行{3})。我們也可以叠代集合,用remove方法依次移除所有的值,但既然有更簡單的方法,那樣做就太麻煩了
this.clear = function(){ items = {}; // {3} };
【size】
size方法(返回集合中有多少項)方法有三種實現方式。 第一種方法是使用一個length變量,每當使用add或remove方法時控制它;第二種方法,使用JavaScript內建的Object類的一個內建函數(ECMAScript 5以上版本):
JavaScript的Object類有一個keys方法,它返回一個包含給定對象所有屬性的數組。在這種情況下,可以使用這個數組的length屬性(行{4})來返回items對象的屬性個數。以下代碼只能在現代瀏覽器中運行
this.size = function(){ return Object.keys(items).length; //{4} };
第三種方法是手動提取items對象的每一個屬性,記錄屬性的個數並返回這個數字。這個方法可以在任何瀏覽器上運行,和之前的代碼是等價的:
遍歷items對象的所有屬性(行{5}),檢查它們是否是對象自身的屬性(避免重復計數—— 行{6})。如果是,就遞增count變量的值(行{7}),最後在方法結束時返回這個數字
[註意]不能簡單地使用for-in語句遍歷items對象的屬性,遞增count變量的值。 還需要使用has方法(以驗證items對象具有該屬性),因為對象的原型包含了額外的屬性(屬性既有繼承自JavaScript的Object類的,也有屬於對象自身,未用於數據結構的)
this.sizeLegacy = function(){ var count = 0; for(var prop in items) { //{5} if(items.hasOwnProperty(prop)) //{6} ++count; //{7} } return count; };
【values】
values方法也應用了相同的邏輯,提取items對象的所有屬性,以數組的形式返回:
this.values = function(){ let values = []; for (let i=0, keys=Object.keys(items); i<keys.length; i++) { values.push(items[keys[i]]); } return values; };
以上代碼只能在現代瀏覽器中運行
如果想讓代碼在任何瀏覽器中都能執行,可以用與之前代碼等價的下面這段代碼:
this.valuesLegacy = function(){ let values = []; for(let key in items) { //{7} if(items.hasOwnProperty(key)) { //{8} values.push(items[key]); } } return values; };
所以,首先遍歷items對象的所有屬性(行{7}),把它們添加一個數組中(行{8}),並返回這個數組。該方法類似於sizeLegacy方法,但我們添加一個數組,而不是計算屬性個數
【使用Set類】
數據結構已經完成了,下面來試著執行一些命令,測試我們的Set類:
var set = new Set(); set.add(1); console.log(set.values()); //輸出["1"] console.log(set.has(1)); //輸出true console.log(set.size()); //輸出1 set.add(2); console.log(set.values()); //輸出["1", "2"] console.log(set.has(2)); //true console.log(set.size()); //2 set.remove(1); console.log(set.values()); //輸出["2"] set.remove(2); console.log(set.values()); //輸出[]
現在我們有了一個和ECMAScript6中非常類似的Set類實現
集合操作
對集合可以進行如下操作
1、並集:對於給定的兩個集合,返回一個包含兩個集合中所有元素的新集合
2、交集:對於給定的兩個集合,返回一個包含兩個集合中共有元素的新集合
3、差集:對於給定的兩個集合,返回一個包含所有存在於第一個集合且不存在於第二個集合的元素的新集合
4、子集:驗證一個給定集合是否是另一集合的子集
【並集】
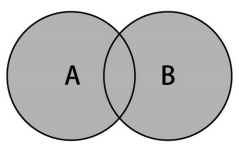
並集的數學概念是集合A和B的並集,表示為A∪B,定義如下:
A∪B = { x | x ∈ A∨x ∈ B }
意思是x(元素)存在於A中,或x存在於B中。下圖展示了並集操作:
現在來實現Set類的union方法:
首先需要創建一個新的集合,代表兩個集合的並集(行{1})。接下來,獲取第一個集合(當前的Set類實例)所有的值(values),遍歷並全部添加到代表並集的集合中(行{2})。然後對第二個集合做同樣的事(行{3})。最後返回結果
this.union = function(otherSet){ let unionSet = new Set(); //{1} let values = this.values(); //{2} for (let i=0; i<values.length; i++){ unionSet.add(values[i]); } values = otherSet.values(); //{3} for (let i=0; i<values.length; i++){ unionSet.add(values[i]); } return unionSet; };
測試一下上面的代碼:
var setA = new Set(); setA.add(1); setA.add(2); setA.add(3); var setB = new Set(); setB.add(3); setB.add(4); setB.add(5); setB.add(6); var unionAB = setA.union(setB); console.log(unionAB.values());
輸出為["1", "2", "3", "4", "5", "6"]。註意元素3同時存在於A和B中,它在結果的 集合中只出現一次
【交集】
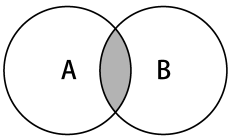
交集的數學概念是集合A和B的交集,表示為A∩B,定義如下:
A∩B = { x | x ∈ A∧x ∈ B }
意思是x(元素)存在於A中,且x存在於B中。下圖展示了交集操作:
現在來實現Set類的intersection方法:
intersection方法需要找到當前Set實例中,所有存在於給定Set實例中的元素。首先創建一個新的Set實例,這樣就能用它返回共有的元素(行{1})。接下來,遍歷當前Set實例所有的值(行{2}),驗證它們是否也存在於otherSet實例(行{3})。可以用前面實現的has方法來驗證元素是否存在於Set實例中。然後,如果這個值也存在於另一個Set實例中,就將其添加到創建的intersectionSet變量中(行{4}),最後返回它。
this.intersection = function(otherSet){ let intersectionSet = new Set(); //{1} let values = this.values(); for (let i=0; i<values.length; i++){ //{2} if (otherSet.has(values[i])){ //{3} intersectionSet.add(values[i]); //{4} } } return intersectionSet; }
測試一下上面的代碼:
var setA = new Set(); setA.add(1); setA.add(2); setA.add(3); var setB = new Set(); setB.add(2); setB.add(3); setB.add(4); var intersectionAB = setA.intersection(setB);
console.log(intersectionAB.values());
輸出為["2", "3"],因為2和3同時存在於兩個集合中
【差集】
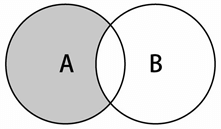
差集的數學概念,集合A和B的差集,表示為A-B,定義如下:
意思是x(元素)存在於A中,且x不存在於B中。下圖展示了集合A和B的差集操作:
現在來實現Set類的difference方法:
intersection方法會得到所有同時存在於兩個集合中的值。而difference方法會得到所有存在於集合A但不存在於B的值。因此這兩個方法在實現上唯一的區別就是行{3}。只獲取不存在於otherSet實例中的值,而不是也存在於其中的值。行{1}、{2}和{4}是完全相同的
this.intersection = function(otherSet){ let intersectionSet = new Set(); //{1} let values = this.values(); for (let i=0; i<values.length; i++){ //{2} if (!otherSet.has(values[i])){ //{3} intersectionSet.add(values[i]); //{4} } } return intersectionSet; }
測試一下上面的代碼:
var setA = new Set(); setA.add(1); setA.add(2); setA.add(3); var setB = new Set(); setB.add(2); setB.add(3); setB.add(4); var differenceAB = setA.difference(setB);
console.log(differenceAB.values());
輸出為["1"],因為1是唯一一個僅存在於setA的元素
【子集】
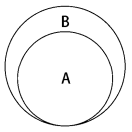
子集的數學概念是集合A是B的子集(或集合B包含了A),表示為A⊆B,定義如下:
∀x { x ∈ A → x ∈ B }
意思是集合A中的每一個x(元素),也需要存在於B中。下圖展示了集合A是集合B的子集:
現在來實現Set類的subset方法:
首先需要驗證的是當前Set實例的大小。如果當前實例中的元素比otherSet實例更多,它就不是一個子集(行{1})。子集的元素個數需要小於或等於要比較的集合。
接下來要遍歷集合中的所有元素(行{2}),驗證這些元素也存在於otherSet中(行{3})。如果有任何元素不存在於otherSet中,就意味著它不是一個子集,返回false(行{4})。如果所有元素都存在於otherSet中,行{4}就不會被執行,那麽就返回true(行{5})。
this.subset = function(otherSet){ if (this.size() > otherSet.size()){ //{1} return false; } else { let values = this.values(); for (let i=0; i<values.length; i++){ //{2} if (!otherSet.has(values[i])){ //{3} return false; //{4} } } return true; //{5} } };
檢驗一下上面的代碼效果如何:
var setA = new Set(); setA.add(1); setA.add(2); var setB = new Set(); setB.add(1); setB.add(2); setB.add(3); var setC = new Set(); setC.add(2); setC.add(3); setC.add(4); console.log(setA.subset(setB)); console.log(setA.subset(setC));
我們有三個集合:setA是setB的子集(因此輸出為true),然而setA不是setC的子集(setC 只包含了setA中的2,而不包含1),因此輸出為false
【完整代碼】
關於集合的完整代碼如下
function Set() { let items = {}; this.add = function(value){ if (!this.has(value)){ items[value] = value; return true; } return false; }; this.delete = function(value){ if (this.has(value)){ delete items[value]; return true; } return false; }; this.has = function(value){ return items.hasOwnProperty(value); //return value in items; }; this.clear = function(){ items = {}; }; /** * Modern browsers function * IE9+, FF4+, Chrome5+, Opera12+, Safari5+ * @returns {Number} */ this.size = function(){ return Object.keys(items).length; }; /** * cross browser compatibility - legacy browsers * for modern browsers use size function * @returns {number} */ this.sizeLegacy = function(){ let count = 0; for(let key in items) { if(items.hasOwnProperty(key)) ++count; } return count; }; /** * Modern browsers function * IE9+, FF4+, Chrome5+, Opera12+, Safari5+ * @returns {Array} */ this.values = function(){ let values = []; for (let i=0, keys=Object.keys(items); i<keys.length; i++) { values.push(items[keys[i]]); } return values; }; this.valuesLegacy = function(){ let values = []; for(let key in items) { if(items.hasOwnProperty(key)) { values.push(items[key]); } } return values; }; this.getItems = function(){ return items; }; this.union = function(otherSet){ let unionSet = new Set(); //{1} let values = this.values(); //{2} for (let i=0; i<values.length; i++){ unionSet.add(values[i]); } values = otherSet.values(); //{3} for (let i=0; i<values.length; i++){ unionSet.add(values[i]); } return unionSet; }; this.intersection = function(otherSet){ let intersectionSet = new Set(); //{1} let values = this.values(); for (let i=0; i<values.length; i++){ //{2} if (otherSet.has(values[i])){ //{3} intersectionSet.add(values[i]); //{4} } } return intersectionSet; }; this.difference = function(otherSet){ let differenceSet = new Set(); //{1} let values = this.values(); for (let i=0; i<values.length; i++){ //{2} if (!otherSet.has(values[i])){ //{3} differenceSet.add(values[i]); //{4} } } return differenceSet; }; this.subset = function(otherSet){ if (this.size() > otherSet.size()){ //{1} return false; } else { let values = this.values(); for (let i=0; i<values.length; i++){ //{2} if (!otherSet.has(values[i])){ //{3} return false; //{4} } } return true; } }; }
【ES6】
ES6版本的代碼如下
let Set2 = (function () { const items = new WeakMap(); class Set2 { constructor () { items.set(this, {}); } add(value){ if (!this.has(value)){ let items_ = items.get(this); items_[value] = value; return true; } return false; } delete(value){ if (this.has(value)){ let items_ = items.get(this); delete items_[value]; return true; } return false; } has(value){ let items_ = items.get(this); return items_.hasOwnProperty(value); } clear(){ items.set(this, {}); } size(){ let items_ = items.get(this); return Object.keys(items_).length; } values(){ let values = []; let items_ = items.get(this); for (let i=0, keys=Object.keys(items_); i<keys.length; i++) { values.push(items_[keys[i]]); } return values; } getItems(){ return items.get(this); } union(otherSet){ let unionSet = new Set(); let values = this.values(); for (let i=0; i<values.length; i++){ unionSet.add(values[i]); } values = otherSet.values(); for (let i=0; i<values.length; i++){ unionSet.add(values[i]); } return unionSet; } intersection(otherSet){ let intersectionSet = new Set(); let values = this.values(); for (let i=0; i<values.length; i++){ if (otherSet.has(values[i])){ intersectionSet.add(values[i]); } } return intersectionSet; } difference(otherSet){ let differenceSet = new Set(); let values = this.values(); for (let i=0; i<values.length; i++){ if (!otherSet.has(values[i])){ differenceSet.add(values[i]); } } return differenceSet; }; subset(otherSet){ if (this.size() > otherSet.size()){ return false; } else { let values = this.values(); for (let i=0; i<values.length; i++){ if (!otherSet.has(values[i])){ return false; } } return true; } }; } return Set2; })();
ES6
ECMAScript 2015新增了Set類。我們可以基於ES6的Set開發我們的Set類
和我們的Set不同,ES6的Set的values方法返回Iterator,而不是值構成的數組。另一個區別是,我們實現的size方法返回set中存儲的值的個數,而ES6的Set則有一個size屬性
let set = new Set(); set.add(1); console.log(set.values()); // 輸出@Iterator console.log(set.has(1)); // 輸出true console.log(set.size); // 輸出1
可以用delete方法刪除set中的元素:
set.delete(1);
clear方法會重置set數據結構,這跟我們實現的功能一樣
【集合】
我們的Set類實現了並集、交集、差集、子集等數學操作,然而ES6原生的Set並沒有這些功能
我們可以創建一個新的集合,用來添加兩個集合中所有的元素(行{1})。叠代這兩個集合(行{2}、行{3}),把所有元素都添加到並集的集合中。代碼如下:
let unionAb = new Set(); //{1} for (let x of setA) unionAb.add(x); //{2} for (let x of setB) unionAb.add(x); //{3}
模擬交集操作需要創建一個輔助函數,來生成包含setA和setB都有的元素的新集合(行 {1})。代碼如下:
let intersection = function(setA, setB) { let intersectionSet = new Set(); for (let x of setA) { if (setB.has(x)) { //{1} intersectionSet.add(x); } } return intersectionSet; }; let intersectionAB = intersection(setA, setB);
交集可以用更簡單的語法實現,代碼如下:
intersectionAb = new Set([x for (x of setA) if (setB.has(x))]);
這和intersection函數的效果完全一樣
交集操作創建的集合包含setA和setB都有的元素,差集操作創建的集合包含的則是setA有 而setB沒有的元素。看下面的代碼:
let difference = function(setA, setB) { let differenceSet = new Set(); for (let x of setA) { if (!setB.has(x)) { //{1} differenceSet.add(x); } } return differenceSet; }; let differenceAB = difference(setA, setB);
intersection函數和difference函數只有行{1}不同,因為差集中只添加setA有而setB 沒有的元素
差集也可以用更簡單的語法實現,代碼如下:
differenceAB = new Set([x for (x of setA) if (!setB.has(x))]);
【set代碼】
基於ES6的set開發的類的完整代碼如下
let set = new Set(); //--------- Union ---------- let unionAb = new Set(); for (let x of setA) unionAb.add(x); for (let x of setB) unionAb.add(x); //--------- Intersection ---------- let intersection = function(setA, setB){ let intersectionSet = new Set(); for (let x of setA){ if (setB.has(x)){ intersectionSet.add(x); } } return intersectionSet; }; let intersectionAB = intersection(setA, setB); //alternative - works on FF only //intersectionAb = new Set([x for (x of setA) if (setB.has(x))]); //--------- Difference ---------- let difference = function(setA, setB){ let differenceSet = new Set(); for (let x of setA){ if (!setB.has(x)){ differenceSet.add(x); } } return differenceSet; }; let differenceAB = difference(setA, setB); //alternative - works on FF only //differenceAB = new Set([x for (x of setA) if (!setB.has(x))]);
前端學數據結構之集合
