這個馬拉車算法Manacher‘s Algorithm是用來查找一個字符串的最長回文子串的線性方法，由一個叫Manacher的人在1975年發明的，這個方法的最大貢獻是在於將時間復雜度提升到了線性，這是非常了不起的。對於回文串想必大家都不陌生，就是正讀反讀都一樣的字符串，比如 "bob", "level", "noon" 等等，那麽如何在一個字符串中找出最長回文子串呢，可以以每一個字符為中心，向兩邊尋找回文子串，在遍歷完整個數組後，就可以找到最長的回文子串。但是這個方法的時間復雜度為O(n*n)，並不是很高效，下面我們來看時間復雜度為O(n)的馬拉車算法。

由於回文串的長度可奇可偶，比如"bob"是奇數形式的回文，"noon"就是偶數形式的回文，馬拉車算法的第一步是預處理，做法是在每一個字符的左右都加上一個特殊字符，比如加上‘#‘，那麽

bob --> #b#o#b#

noon --> #n#o#o#n#

這樣做的好處是不論原字符串是奇數還是偶數個，處理之後得到的字符串的個數都是奇數個，這樣就不用分情況討論了，而可以一起搞定。接下來我們還需要和處理後的字符串t等長的數組p，其中p[i]表示以t[i]字符為中心的回文子串的半徑，若p[i] = 1，則該回文子串就是t[i]本身，那麽我們來看一個簡單的例子：

# 1 # 2 # 2 # 1 # 2 # 2 #
1 2 1 2 5 2 1 6 1 2 3 2 1

由於第一個和最後一個字符都是#號，且也需要搜索回文，為了防止越界，我們還需要在首尾再加上非#號字符，實際操作時我們只需給開頭加上個非#號字符，結尾不用加的原因是字符串的結尾標識為‘\0‘，等於默認加過了。通過p數組我們就可以找到其最大值和其位置，就能確定最長回文子串了，那麽下面我們就來看如何求p數組，需要新增兩個輔助變量mx和id，其中id為最大回文子串中心的位置，mx是回文串能延伸到的最右端的位置，這個算法的最核心的一行如下：

p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;

可以這麽說，這行要是理解了，那麽馬拉車算法基本上就沒啥問題了，那麽這一行代碼拆開來看就是

如果mx > i, 則 p[i] = min(p[2 * id - i], mx - i)

否則， p[i] = 1

當 mx - i > P[j] 的時候，以S[j]為中心的回文子串包含在以S[id]為中心的回文子串中，由於 i 和 j 對稱，以S[i]為中心的回文子串必然包含在以S[id]為中心的回文子串中，所以必有 P[i] = P[j]，見下圖。

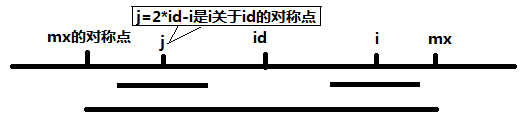
當 P[j] >= mx - i 的時候，以S[j]為中心的回文子串不一定完全包含於以S[id]為中心的回文子串中，但是基於對稱性可知，下圖中兩個綠框所包圍的部分是相同的，也就是說以S[i]為中心的回文子串，其向右至少會擴張到mx的位置，也就是說 P[i] >= mx - i。至於mx之後的部分是否對稱，就只能老老實實去匹配了。

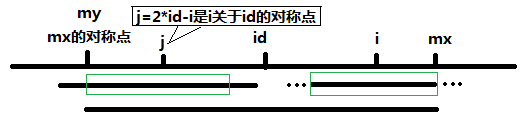
對於 mx <= i 的情況，無法對 P[i]做更多的假設，只能P[i] = 1，然後再去匹配了。

參見如下實現代碼：

#include <vector>
#include <iostream>
#include <string>

using namespace std;

string Manacher(string s) {
    // Insert ‘#‘
    string t = "$#";
    for (int i = 0; i < s.size(); ++i) {
        t += s[i];
        t += "#";
    }
    // Process t
    vector<int> p(t.size(), 0);
    int mx = 0, id = 0, resLen = 0, resCenter = 0;
    for (int i = 1; i < t.size(); ++i) {
        p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;
        while (t[i + p[i]] == t[i - p[i]]) ++p[i];
        if (mx < i + p[i]) {
            mx = i + p[i];
            id = i;
        }
        if (resLen < p[i]) {
            resLen = p[i];
            resCenter = i;
        }
    }
    return s.substr((resCenter - resLen) / 2, resLen - 1);
}

int main() {
    string s1 = "12212";
    cout << Manacher(s1) << endl;
    string s2 = "122122";
    cout << Manacher(s2) << endl;
    string s = "waabwswfd";
    cout << Manacher(s) << endl;
}

Manacher's Algorithm 馬拉車算法