題目描述

在一個 n*m 的棋盤上，每個格子有一個權值，初始時，在某個格子的頂點處一只面朝北的螞蟻，我們只知道它的行走路線是如何轉彎，卻不知道每次轉彎前走了多長。

螞蟻轉彎是有一定特點的，即它的轉彎序列一定是如下的形式：右轉，右轉，左轉，左轉，右轉，右轉…左轉，左轉，右轉，右轉，右轉。即兩次右轉和兩次左轉交替出現的形式，最後兩次右轉（最後兩次一定是右轉）後再多加一次右轉。我們還知道，螞蟻不會在同一個位置連續旋轉兩次，並且螞蟻行走的路徑除了起點以外，不會到達同一個點多次，它最後一定是回到起點然後結束自己的行程，而且螞蟻只會在棋盤格子的頂點處轉彎。

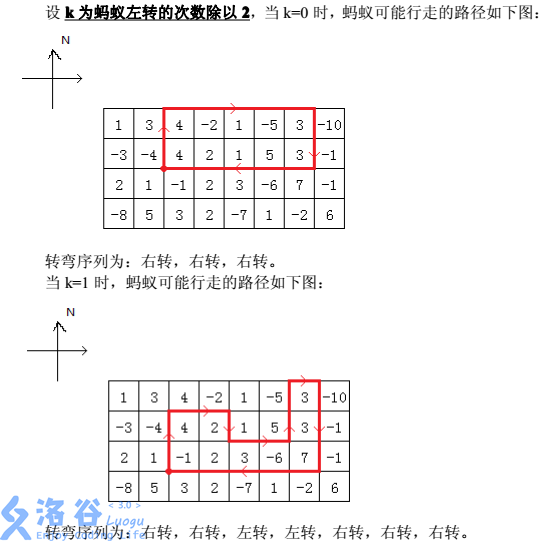
現在已知棋盤大小、每個格子的權值以及左轉次數/2 的值，問螞蟻走出的路徑圍出的封閉圖形，權值之和最大可能是多少。

輸入輸出格式

輸入格式：

在輸入文件ant.in 中，第一行三個數n,m,k。意義如題目描述。

接下來一個n 行m 列的整數矩陣，表示棋盤。

輸出格式：

一個數，表示螞蟻所走路徑圍出的圖形可能的最大權值和。

輸入輸出樣例

2 5 2
-1 -1 -1 -1 -1
-1 -1 -1 -1 -1

-8

說明

【樣例說明】

除了第一行的第二個和第一行的第四個都要圍起來才至少合法。

【數據規模與約定】

10%的數據所有格子中權值均非負

另20%的數據n=2

另30%的數據k=0

100%的數據1≤n≤100,1≤m≤100,0≤k≤10 保證存在合法路徑，數據有梯度，格子中每個元素的值絕對值不超過 10000

P3335 這個題思維難度還是有的。。(至少我是這麽想的。。大佬就別吐槽我了)

首先，通過題目描述，我們可以在紙上畫一畫，可以發現，圖像一定是像長城一樣的

就是好多個矩形它們的底在一條直線上，高和寬不同，而且，還有一點就是它是高低相間的

而且由右轉形成高峰，由左轉形成低谷。

那麽我們可以枚舉圖的右下角(i,j)，那麽有兩種情況：

一:第j-1列和第j列在同一個矩形裏；

二:第j-1列和第j列在不同的矩形裏；

我們要記錄的狀態與點(i,j),p(指的是當前枚舉的是第p個矩形),h(當前枚舉的舉行高度為i-h+1)有關

所以用f[i][j][p][h]來記錄‘一’情況的狀態，用g[i][j][p][h][0/1]來記錄‘二’情況的狀態

這裏0表示上一個矩形高度高於h，1表示低於h；

那麽轉移就好寫了：

f[i][j][p][h]=max(f[i][j-1][p][h],g[i][j-1][p-1][h][p%2])+s[i][j]-s[h-1][j];

對了，這裏這個s數組求的是每一列的前綴和，可以在輸入中預處理出來，方便計算用；

關於g數組的維護，我們已經維護出f數組的第j列了

那麽這一列所在的矩形要麽是低谷，要麽是高峰，我們都要考慮

->高峰：

g[i][j][p][h][0]=max(f[i][j][p][h-1],g[i][j][p][h-1][0]);

->低谷：

g[i][j][p][h][1]=max(f[i][j][p][h+1],g[i][j][p][h+1][1]);

當然我們可以在計算過程中更新答案，還可以省掉i這一維

因為從方程中就可以看出來i其實沒有參與轉移

 1 #pragma GCC optimize(2)
 2 #pragma G++ optimize(2)
 3 #pragma GCC target ("avx")
 4 #include<iostream>
 5 #include<algorithm>
 6 #include<cmath>
 7 #include<cstdio>
 8 #include<cstring>
 9 using namespace std;
10 const int maxn=120;
11 const int Inf=1000000001; 
12 int n,m,k,ans;
13 int a[maxn][maxn];
14 int f[maxn][25][maxn];
15 int g[maxn][25][maxn][2];
16 int s[maxn][maxn];
17 void ini()
18 {
19     scanf("%d%d%d",&n,&m,&k);
20     //因為有2*k次左轉，所以總矩形數就是k*2+1 
21     k=k*2+1;
22     for(int i=1;i<=n;i++)
23     {
24         for(int j=1;j<=m;j++)
25         {
26             scanf("%d",&a[i][j]);
27             s[i][j]=s[i-1][j]+a[i][j];
28         }
29     }
30     //預處理 因為要求最大值，所以邊界賦值為-Inf； 
31     for(int p=1;p<=k;p++)
32     {
33         for(int h=1;h<=n;h++)
34         {
35             f[0][p][h]=-Inf;
36             g[0][p][h][0]=-Inf;
37             g[0][p][h][1]=-Inf;
38         }
39     }
40 }
41 void dp()
42 {
43     ans=-Inf;
44     for(int i=1;i<=n;i++)
45     {
46         for(int j=1;j<=m;j++)
47         {
48             for(int p=1;p<=k;p++)
49             {
50                 for(int h=i;h>=1;h--)//維護f數組 
51                 {
52                     f[j][p][h]=max(f[j-1][p][h],g[j-1][p-1][h][p%2])+s[i][j]-s[h-1][j];
53                 }
54                 //維護g數組 
55                 g[j][p][1][0]=-Inf;
56                 //0指當前矩形比下一個高，所以從高到低更新，才可以確保取最大值的矩形一定是高的 
57                 for(int h=2;h<=i;h++)
58                 {
59                     g[j][p][h][0]=max(f[j][p][h-1],g[j][p][h-1][0]);
60                 }
61                 g[j][p][i][1]=-Inf;
62                 //1指當前矩形比下一個底，所以從低到高更新，才可以確保取最大值的矩形一定是低的
63                 for(int h=i-1;h>=1;h--)
64                 {
65                     g[j][p][h][1]=max(f[j][p][h+1],g[j][p][h+1][1]);
66                 }
67             }
68             //更新答案，因為最後一列一定是高的，所以用0轉移； 
69             ans=max(ans,max(f[j][k][i],g[j][k][i][0]));
70         }
71     }
72 }
73 int main()
74 {
75     ini();//讀入一些數據 
76     dp();
77     printf("%d\n",ans);
78     return 0;
79 }

bzoj 3111 螞蟻 動態規劃