【PTA-天梯賽訓練】六度空間(廣搜)
阿新 • • 發佈:2018-03-16
六度空間 style lan 輸出 back pty ima 格式 網上 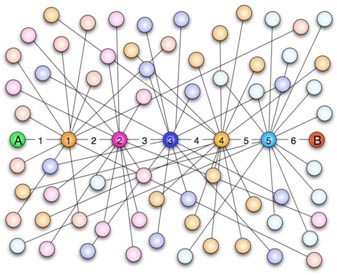
圖1 六度空間示意圖輸出樣例:
“六度空間”理論又稱作“六度分隔(Six Degrees of Separation)”理論。這個理論可以通俗地闡述為:“你和任何一個陌生人之間所間隔的人不會超過六個,也就是說,最多通過五個人你就能夠認識任何一個陌生人。”如圖1所示。

圖1 六度空間示意圖
“六度空間”理論雖然得到廣泛的認同,並且正在得到越來越多的應用。但是數十年來,試圖驗證這個理論始終是許多社會學家努力追求的目標。然而由於歷史的原因,這樣的研究具有太大的局限性和困難。隨著當代人的聯絡主要依賴於電話、短信、微信以及因特網上即時通信等工具,能夠體現社交網絡關系的一手數據已經逐漸使得“六度空間”理論的驗證成為可能。
假如給你一個社交網絡圖,請你對每個節點計算符合“六度空間”理論的結點占結點總數的百分比。
輸入格式:
輸入第1行給出兩個正整數,分別表示社交網絡圖的結點數N(1<N≤104,表示人數)、邊數M(≤33*N,表示社交關系)。隨後的M行對應M條邊,每行給出一對正整數,分別是該條邊直接連通的兩個結點的編號(節點從1到N編號)。
輸出格式:
對每個結點輸出與該結點距離不超過6的結點數占結點總數的百分比,精確到小數點後2位。每個結節點輸出一行,格式為“結點編號:(空格)百分比%”。
輸入樣例:
10 9
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
輸出樣例:
1: 70.00% 2: 80.00% 3: 90.00% 4: 100.00% 5: 100.00% 6: 100.00% 7: 100.00% 8: 90.00% 9: 80.00% 10: 70.00%
思路:深搜過不了,因為會爆棧,只能用廣搜了。
#include<bits/stdc++.h> using namespace std; int vis[10005],n,m; vector<int>G[10005]; //vector類型的二維數組,保存每個點下一次所能接觸的所有元素 struct node { int x,d; //x-點 d-深度 }a; //a 結構體 int bfs(int x,int s) //s記為認識的人數 ,不定義s的值,s的值就是1(自己) { int i,D; queue<node>q; q.push(node{x,0}); //將第一個點x和深度0的結構體壓入隊列q,tip:只有一次 while(!q.empty()) //隊列不為空 { a=q.front(); //結構體 a 是隊首元素 q.pop(); //再刪除隊首元素 D=a.d+1; //深度+1 for(i=0;i<G[a.x].size();i++) //每一行 { int X=G[a.x][i]; //X為每一行的各元素 if(!vis[X]&&D<=6) //未被訪問過且深度小於等於6 { vis[X]=1; s++; q.push(node{X,D}); //推入一個點為X,深度為D的結構體 } } } return s; } int main() { int i,u,v; scanf("%d%d",&n,&m); while(m--) { scanf("%d%d",&u,&v); G[u].push_back(v); //建立u-v結點之間的聯系 G[v].push_back(u); } for(i=1;i<=n;i++) { memset(vis,0,sizeof vis); vis[i]=1; printf("%d: %.2lf%%\n",i,bfs(i,1)*100.0/n); } return 0; }
【PTA-天梯賽訓練】六度空間(廣搜)
