#1184 : 連通性二·邊的雙連通分量

描述

在基本的網絡搭建完成後，學校為了方便管理還需要對所有的服務器進行編組，網絡所的老師找到了小Hi和小Ho，希望他倆幫忙。

老師告訴小Hi和小Ho：根據現在網絡的情況，我們要將服務器進行分組，對於同一個組的服務器，應當滿足：當組內任意一個連接斷開之後，不會影響組內服務器的連通性。在滿足以上條件下，每個組內的服務器數量越多越好。

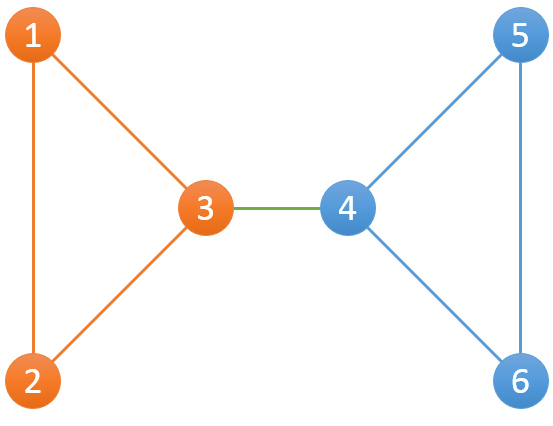
比如下面這個例子，一共有6個服務器和7條連接：

其中包含2個組，分別為{1,2,3},{4,5,6}。對{1,2,3}而言，當1-2斷開後，仍然有1-3-2可以連接1和2；當2-3斷開後，仍然有2-1-3可以連接2和3；當1-3斷開後，仍然有1-2-3可以連接1和3。{4,5,6}這組也是一樣。

老師把整個網絡的情況告訴了小Hi和小Ho，小Hi和小Ho要計算出每一臺服務器的分組信息。

提示：邊的雙連通分量

輸入

第1行：2個正整數，N,M。表示點的數量N，邊的數量M。1≤N≤20,000, 1≤M≤100,000

第2..M+1行：2個正整數，u,v。表示存在一條邊(u,v)，連接了u,v兩臺服務器。1≤u<v≤N

保證輸入所有點之間至少有一條連通路徑。

輸出

第1行：1個整數，表示該網絡的服務器組數。

第2行：N個整數，第i個數表示第i個服務器所屬組內，編號最小的服務器的編號。比如分為{1,2,3},{4,5,6}，則輸出{1,1,1,4,4,4}；若分為{1,4,5},{2,3,6}則輸出{1,2,2,1,1,2}

代碼

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<vector>
 5 #include<stack>
 6 #include<algorithm>
 7 using namespace std;
 8 const int N=2e4+5;
 9 vector<int>v[N];
10 stack<int>sk;
11 int num,cnt;
12 int low[N],dfn[N],fa[N],ans[N];
 
13 
14 void init(){
15     cnt=num=0;
16     memset(dfn,0,sizeof(dfn));
17     memset(low,0,sizeof(low));
18     memset(fa,0,sizeof(fa));
19     memset(ans,0,sizeof(ans));
20 }
21 
22 void dfs(int u,int f){
23     low[u]=dfn[u]=++cnt;
24     sk.push(u);
25     for(int i=0;i<v[u].size();i++){
26         int t=v[u][i];
27         if(!dfn[t]){
28             dfs(t,u);
29             low[u]=min(low[u],low[t]);
30         }
31         else if(t!=f) low[u]=min(low[u],dfn[t]);      //無向圖不需要判斷是否在棧中
32     }
33     // 因為low[u] == dfn[u]，對(parent[u],u)來說有dfn[u] > dfn[ parent[u] ]，因此low[u] > dfn[ parent[u] ]
34     // 所以(parent[u],u)一定是一個橋，那麽此時棧內在u之前入棧的點和u被該橋分割開
35     // 則u和之後入棧的節點屬於同一個組
36     //最後剩下的一個(或者說第一個)組雖然前面沒有割邊，但是也適用於這個判斷
37     if(low[u]==dfn[u]){
38         ++num;
39         while(!sk.empty()){
40             int t=sk.top();
41             sk.pop();
42             fa[t]=num;
43             if(ans[num]==0||ans[num]>t)
44                 ans[num]=t;
45             if(t==u)
46                 break;
47         }
48     }
49 }
50 
51 int main(){
52     int n,m;
53     while(~scanf("%d%d",&n,&m)){
54         init();
55         for(int i=1;i<=m;i++){
56             int a,b;
57             scanf("%d%d",&a,&b);
58             v[a].push_back(b);
59             v[b].push_back(a);
60         }
61         dfs(1,-1);
62         printf("%d\n",num);
63         for(int i=1;i<=n;i++){
64             printf("%d%c",ans[fa[i]],i==n?‘\n‘:‘ ‘);
65         }
66     }
67     return 0;
68 }

hihoCoder #1184 : 連通性二·邊的雙連通分量（邊的雙連通分量模板）