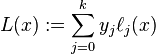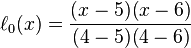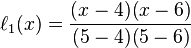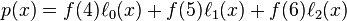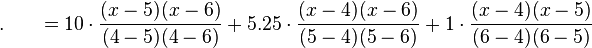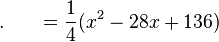一，介紹

　　學過FFT的人都應該知道什麽叫做插值，插值的意思就是說將一個多項式從點值表達轉變成系數表達。

　　在FFT的插值中為什麽可以做到n log n，是因為單位復數根的關系。

　　那對於普通的插值應該怎麽辦呢？解方程是一種方法，但是這個在計算機中十分不現實。

　　所以有許多種插值的方法，其中比較普及的就是拉格朗日插值。

二，定義

　　　對某個多項式函數，已知有給定的k + 1個取值點：

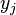　　　其中對應著自變量的位置，而對應著函數在這個位置的取值。

　　　假設任意兩個不同的xj都互不相同，那麽應用拉格朗日插值公式所得到的拉格朗日插值多項式為：

　　　其中每個為拉格朗日基本多項式（或稱插值基函數），其表達式為：

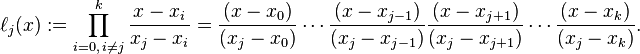[3]

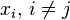　　　拉格朗日基本多項式的特點是在上取值為1，在其它的點上取值為0。

三，例子

　　　假設有某個二次多項式函數，已知它在三個點上的取值為：

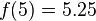
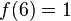
　　　要求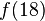的值。

　　　首先寫出每個拉格朗日基本多項式：

　　　然後應用拉格朗日插值法，就可以得到的表達式（為函數的插值函數）：

　　　此時代入數值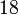就可以求出所需之值：。

四，證明唯一性

　　就是說n+1個點對應的n次多項式只有一個，這個需要證明，但是一般都會直接當成結論，所以不需要去記憶。

五，優點和缺點

　　拉格朗日插值法的公式結構整齊緊湊，在理論分析中十分方便，然而在計算中，當插值點增加或減少一個時，所對應的基本多項式就需要全部重新計算，

　　於是整個公式都會變化，非常繁瑣[5]。這時可以用重心拉格朗日插值法或牛頓插值法來代替。此外，當插值點比較多的時候，拉格朗日插值多項式的次數

　　可能會很高，因此具有數值不穩定的特點，也就是說盡管在已知的幾個點取到給定的數值，但在附近卻會和“實際上”的值之間有很大的偏差（如右下圖）[6]。

　　這類現象也被稱為龍格現象，解決的辦法是分段用較低次數的插值多項式。

拉格朗日插值