題目描述

今年夏天，NOI在SZ市迎來了她30周歲的生日。

來自全國 n 個城市的OIer們都會從各地出發，到SZ市參加這次盛會。

全國的城市構成了一棵以SZ市為根的有根樹，每個城市與它的父親用道路連接。

為了方便起見，我們將全國的 n 個城市用 1 到 n 的整數編號。其中SZ市的編號為 1。

對於除SZ市之外的任意一個城市 v，我們給出了它在這棵樹上的父親城市 fv 以及到父親城市道路的長度 sv。

從城市 v 前往SZ市的方法為：選擇城市 v 的一個祖先 a，支付購票的費用，乘坐交通工具到達 a。

再選擇城市 a 的一個祖先 b，支付費用並到達 b。以此類推，直至到達SZ市。

對於任意一個城市 v，我們會給出一個交通工具的距離限制 lv。

對於城市 v 的祖先 a，只有當它們之間所有道路的總長度不超過 lv 時，從城市 v 才可以通過一次購票到達城市 a，否則不能通過一次購票到達。

對於每個城市 v，我們還會給出兩個非負整數 pv,qv 作為票價參數。

若城市 v 到城市 a 所有道路的總長度為 d，那麽從城市 v 到城市 a 購買的票價為 d * pv+qv。

每個城市的OIer都希望自己到達SZ市時，用於購票的總資金最少。

你的任務就是，告訴每個城市的OIer他們所花的最少資金是多少。

輸入輸出格式

輸入格式：

第 1 行包含2個非負整數 n,t，分別表示城市的個數和數據類型（其意義將在後面提到）。

輸入文件的第 2 到 n 行，每行描述一個除SZ之外的城市。

其中第 v 行包含 5 個非負整數 f_v,s_v,p_v,q_v,l_v，分別表示城市 v 的父親城市，它到父親城市道路的長度，票價的兩個參數和距離限制。

請註意：輸入不包含編號為 1 的SZ市，第 2 行到第 n 行分別描述的是城市 2 到城市 n。

輸出格式：

輸出包含 n-1 行，每行包含一個整數。

其中第 v 行表示從城市 v+1 出發，到達SZ市最少的購票費用。

同樣請註意：輸出不包含編號為 1 的SZ市。

輸入輸出樣例

7 3 
1 2 20 0 3 
1 5 10 100 5 
2 4 10 10 10 
2 9 1 100 10 
3 5 20 100 10 
4 4 20 0 10 
 

40 
150 
70 
149 
300 
150

說明

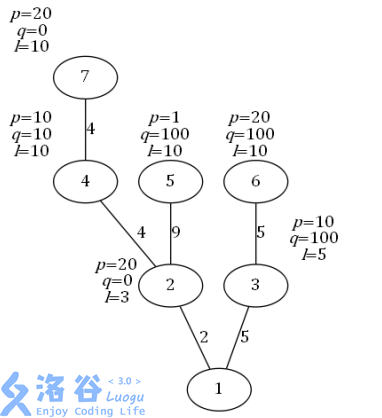
從每個城市出發到達 SZ的路線如下（其中箭頭表示一次直達）：

城市 2：只能選擇 2 → 1，花費為 2 × 20 + 0 = 40。

城市 3：只能選擇 3 → 1，花費為 5 × 10 + 100 = 150。 城 市 4 ： 由 於 4 + 2 =6 ≤ l4 = 10，故可以選擇 4 →1。

若選擇 4 → 1，花費為 (4 +2) × 10 + 10 = 70 ； 若選 擇 4 → 2 → 1，則花費為 (4 ×10 + 10) + (2 × 20 + 0) =90；因此選擇 4 → 1。

城市 5：只能選擇 5 →2 → 1 ， 花費為 (9 × 1 +100) + (2 × 20 + 0) = 149；無法選擇 5 → 1，因為 l5 =10，而城市 5 到城市 1 總路程為 9 + 2 = 11 > 5，城市 5 不能直達城市 1。

城市 6：若選擇 6 → 1，花費為 (5 + 5) × 20 + 100 = 300；若選擇 6 → 3 →1，花費為 (5 × 20 + 100) + (5 × 10 + 100) = 350；因此選擇 6 → 1。

城市 7：選擇 7 → 4 → 1，花費為 (4 × 20 + 0) + ((4 + 2) × 10 + 10) = 150；

其他方案均比該方案差。

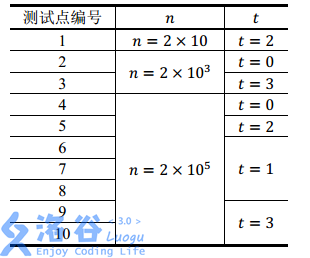
數據規模

這樣子擓題面好像快一點。。。。

斜率優化樹形DP，比較容易看出

怎麽維護距離限制？

（更詳細地後面再寫）

1.樹鏈剖分

2.可持久化（主席樹+單調隊列)

3.可持久化（主席樹+平衡樹）

4.點分治+CDQ分治

5.點分治+sort（my way）

6.點分治+可持久化平衡樹

[NOI2014]購票 --- 斜率優化 + 樹形DP + 數據結構