[golang] 數據結構-樹形選擇排序(錦標賽排序)
阿新 • • 發佈:2018-07-15
節點 UNC sele href 向上 inno make 所有 lse 接上文 簡單選擇排序
簡單選擇排序很容易理解,代碼也很容易實現。但畢竟比較次數太多。樹形選擇排序則對這個問題進行了改進。
簡單選擇排序很容易理解,代碼也很容易實現。但畢竟比較次數太多。樹形選擇排序則對這個問題進行了改進。
原理
簡單來說,樹形選擇排序(Tree selection sort)就是在選擇完一輪找出最小值後,直接在與最小值比較中稍大的元素裏篩選出最小的。這樣避免了簡單選擇查詢那種,拋棄了之前比較過的結果,每次都全部重新比較的情況。
流程舉例
-
先列出所有待排序的元素如:8、4、12、7、35、9、22,並用他們組成滿二叉樹的葉子元素,不足的位置以∞作為補充。
將元素兩兩相比較,分別得到較小值:4,7,9,22。再次兩兩比較,得到4,9。最終比較一次得到最小值4。由此構建出一個完整的滿二叉樹: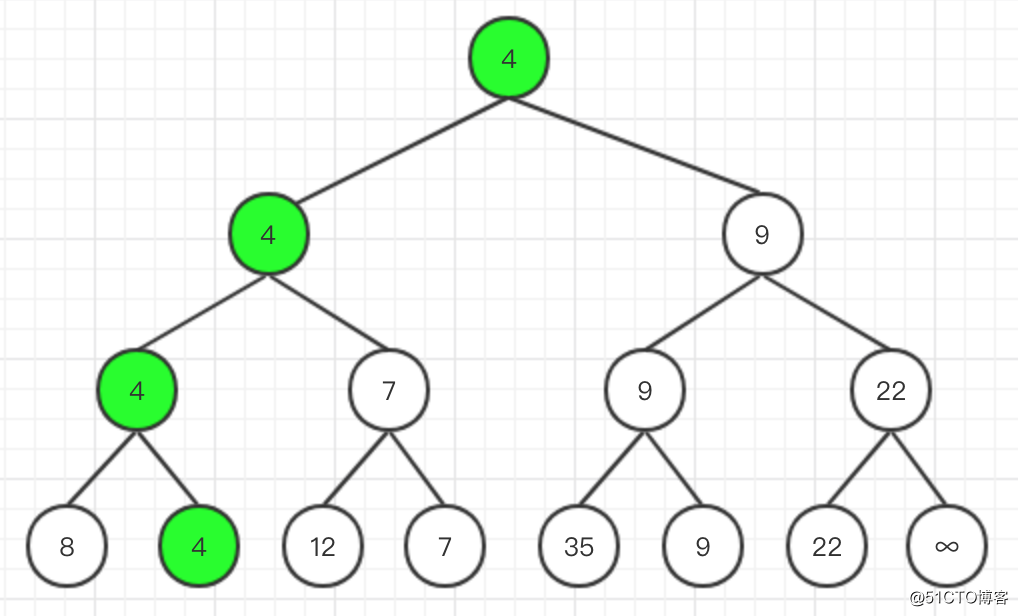
-
完成一輪比較後,將勝出者4的葉子節點改成∞,然後由它的兄弟節點8繼續參加下一輪比較。從這次開始,元素8僅需按構建好的樹結構一步步向上與其他勝出的非父節點僅需比較即可,比如這裏只需要在和7,9比較,就能得到最小元素是7
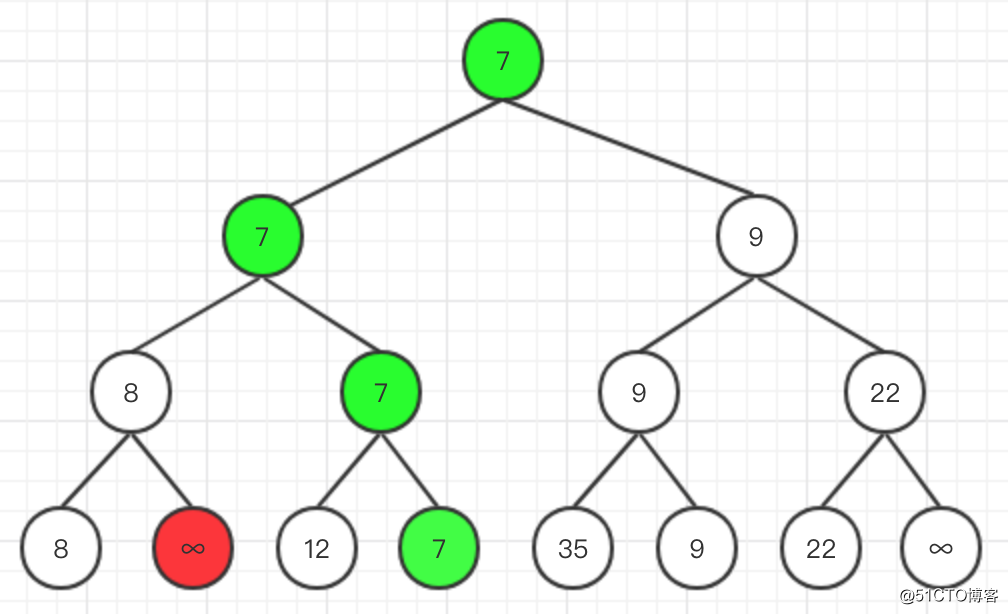
-
然後將元素7的葉子節點改成∞,其兄弟節點12與8、9節點比較,即可得到8:
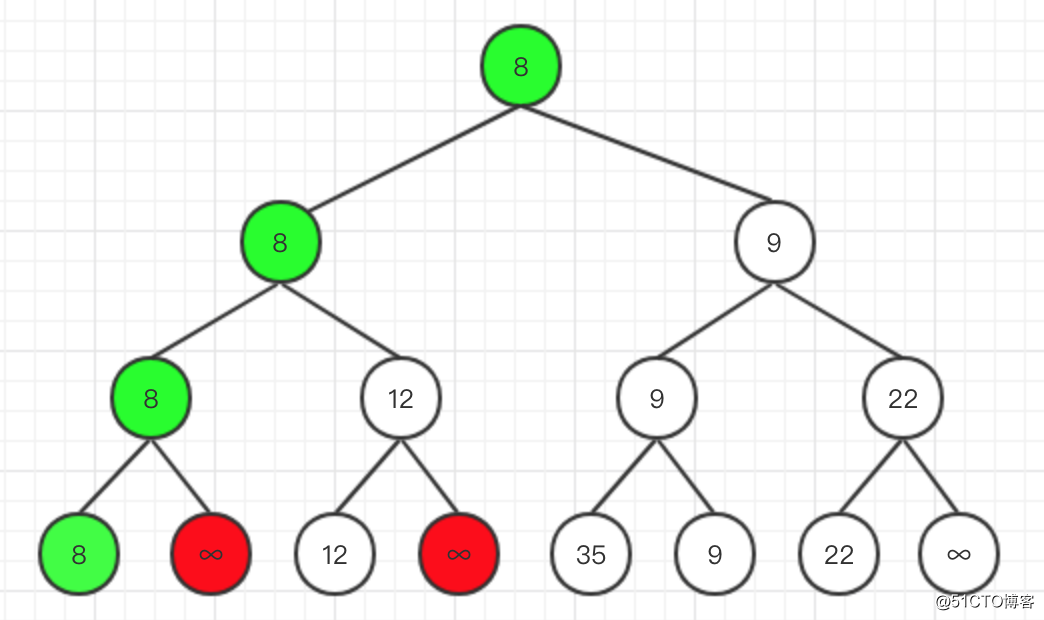
- 以此類推,最終得到最後一個元素35:

時間復雜度
由於每次僅需與勝出的其他節點僅需比較,所以時間復雜度相較簡單選擇排序的O(n^2)降低到O(nlogn)。
但是由於儲存了每次各勝出節點的數據,所以需要更多的儲存空間,而且其中n-1次的與∞的比較行為較為多余。
代碼實現
package main import ( "fmt" "math" ) // 聲明一個節點的結構體,包含節點數值大小和是否需要參與比較 type node struct { // 數值大小 value int // 葉子節點狀態 available bool // 葉子中的排序,方便失效 rank int } func main() { var length = 10 var mm = make(map[int]int, length) var o []int // 先準備一個順序隨機的數(qie)組(pian) for i := 0; i < length; i++ { mm[i] = i } for k, _ := range mm { o = append(o, k) } fmt.Println(o) treeSelectionSort(o) } func treeSelectionSort(origin []int) []int { // 樹的層數 var level int var result = make([]int, 0, len(origin)) for pow(2, level) < len(origin) { level++ } // 葉子節點數 var leaf = pow(2, level) var tree = make([]node, leaf*2-1) // 先填充葉子節點的數據 for i := 0; i < len(origin); i++ { tree[leaf+i-1] = node{origin[i], true, i} } // 每層都比較葉子兄弟大小,選出較大值作為父節點 for i := 0; i < level; i++ { // 當前層節點數 nodeCount := pow(2, level-i) // 每組兄弟間比較 for j := 0; j < nodeCount/2; j++ { compareAndUp(&tree, nodeCount-1+j*2) } } // 這個時候樹頂端的就是最小的元素了 result = append(result, tree[0].value) fmt.Println(result) // 選出最小的元素後,還剩n-1個需要排序 for t := 0; t < len(origin) - 1; t++ { // 贏球的節點 winNode := tree[0].rank + leaf - 1 // 把贏球的葉子節點狀態改為失效 tree[winNode].available = false // 從下一輪開始,只需與每次勝出節點的兄弟節點進行比較 for i := 0; i < level; i ++ { leftNode := winNode if winNode%2 == 0 { leftNode = winNode - 1 } // 比較兄弟節點間大小,並將勝出的節點向上傳遞 compareAndUp(&tree, leftNode) winNode = (leftNode - 1) / 2 } // 每輪都會吧最小的推到樹頂端 result = append(result, tree[0].value) fmt.Println(result) } return origin } func compareAndUp(tree *[]node, leftNode int) { rightNode := leftNode + 1 // 除非左節點無效或者右節點有效並且比左節點大,否則就無腦選左節點 if !(*tree)[leftNode].available || ((*tree)[rightNode].available && (*tree)[leftNode].value > (*tree)[rightNode].value) { (*tree)[(leftNode-1)/2] = (*tree)[rightNode] } else { (*tree)[(leftNode-1)/2] = (*tree)[leftNode] } } func pow(x, y int) int { return int(math.Pow(float64(x), float64(y))) }
運行結果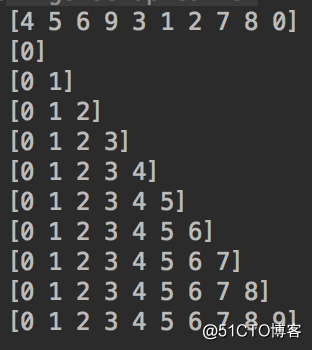
[golang] 數據結構-樹形選擇排序(錦標賽排序)
