題目傳送門

題目描述

你在一家 IT 公司為大型寫字樓或辦公樓(offices)的計算機數據做備份。然而數據備份的工作是枯燥乏味的，因此你想設計一個系統讓不同的辦公樓彼此之間互相備份，而你則坐在家中盡享計算機遊戲的樂趣。

已知辦公樓都位於同一條街上。你決定給這些辦公樓配對(兩個一組)。每一對辦公樓可以通過在這兩個建築物之間鋪設網絡電纜使得它們可以互相備份。

然而，網絡電纜的費用很高。當地電信公司僅能為你提供 K 條網絡電纜，這意味著你僅能為 K 對辦公樓(或總計 2K 個辦公樓)安排備份。任一個辦公樓都屬於唯一的配對組(換句話說，這 2K 個辦公樓一定是相異的)。

此外，電信公司需按網絡電纜的長度(公裏數)收費。因而，你需要選擇這 K對辦公樓使得電纜的總長度盡可能短。換句話說，你需要選擇這 K 對辦公樓，使得每一對辦公樓之間的距離之和(總距離)盡可能小。

下面給出一個示例，假定你有 5 個客戶，其辦公樓都在一條街上，如下圖所示。這 5 個辦公樓分別位於距離大街起點 1km, 3km, 4km, 6km 和 12km 處。電信公司僅為你提供 K=2 條電纜。

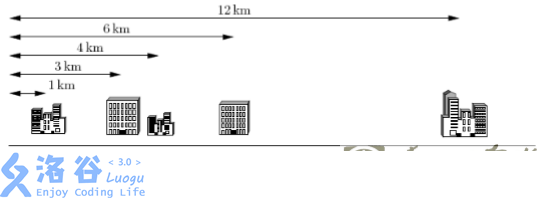
上例中最好的配對方案是將第 1 個和第 2 個辦公樓相連，第 3 個和第 4 個辦公樓相連。這樣可按要求使用 K=2 條電纜。第 1 條電纜的長度是 3km―1km = 2km，第 2 條電纜的長度是 6km―4km = 2 km。這種配對方案需要總長 4km 的網絡電纜，滿足距離之和最小的要求。

輸入輸出格式

輸入格式：

輸入文件的第一行包含整數 n 和 k，其中 n(1≤n≤100 000)表示辦公樓的數目，k(1≤k≤n/2)表示可利用的網絡電纜的數目。

接下來的 n 行每行僅包含一個整數(0≤s≤1000 000 000), 表示每個辦公樓到大街起點處的距離。這些整數將按照從小到大的順序依次出現。

輸出格式：

輸出文件應當由一個正整數組成，給出將 2K 個相異的辦公樓連成 K 對所需的網絡電纜的最小總長度。

輸入輸出樣例

5 2 
1 
3 
4 
6 
12 

4

說明

30%的輸入數據滿足 n≤20。

60%的輸入數據滿足 n≤10 000

　　分析：易證，最優解中配對的大樓一定是相鄰的，就可以將每兩棟相鄰的大樓之間的距離Di求出來，就可以將問題轉化為:[有n-1個元素的數列Di，從中取出k個數，使得這k個數的和最小，並且相鄰的數不能同時選]。

　　再從簡單的情況開始分析：

　　如果k=1，那麽直接選最小的元素。

　　如果k=2，那麽要麽選最小的元素D[i]和除了D[i-1],D[i],D[i+1]以外的最小的元素，要麽選擇D[i]兩邊的元素即D[i-1]和D[i+1]

　　那麽由第二種情況就可以分析得到，對於當前數列中的元素，要麽一定要選最小元素D[i]，要麽就一定要選最小元素兩邊的元素D[i-1],D[i+1]。也就是說，最小元素左右兩側的元素要麽同時被選，要麽同時不選。。那麽就可以先選出D[]中最小的元素D[i]，然後將D[i-1],D[i],D[i+1]從數列中刪除，並在原位置插入一個新元素D[i-1]+D[i+1]-D[i]，然後重復操作即可。（因為如果在後面的操作中選擇了D[i-1]+D[i+1]-D[i]這個元素，就相當於去掉已選擇的結果中的D[i]換上D[i-1]+D[i+1]，如果後面沒選該元素，則選擇D[i]是一步最優策略）

　　那算法也就可以推導出了：建立一個鏈表L和一個小根堆H，L中有n-1個元素，每個元素與小根堆中的每一個元素成一一映射關系，它們的元素都是D[i]，也就是每兩棟樓之間的距離。取出堆頂，將權值累加到答案上，再將堆頂x刪除，同時將x的左右兩側的元素pre[x],nxt[x]刪除，在同樣的位置插入一個新元素p，p的權值D[p]=D[pre[x]]+D[nxt[x]]-D[x]，再在鏈表的對應位置中插入對應的節點p。重復k次即可。

　　不過實際操作的時候有很多細節要註意，具體細節看代碼吧。

　　Code：

 1 //It is made by HolseLee on 10th May 2018
 2 //Luogu.org P3620
 3 #include<bits/stdc++.h>
 4 #define Fi(i,a,b) for(int i=a;i<=b;i++)
 5 using namespace std;
 6 const int N=2e5+7;
 7 int n,k,size,heap[N],fheap[N];
 8 int num[N],nxt[N],pre[N],ans;
 9 inline int read()
10 {
11   char ch=getchar();int num=0;bool flag=false;
12   while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)flag=true;ch=getchar();}
13   while(ch>=‘0‘&&ch<=‘9‘){num=num*10+ch-‘0‘;ch=getchar();}
14   return flag?-num:num;
15 }
16 inline void delet(int x)
17 {
18   heap[x]=heap[size--];
19   fheap[heap[size+1]]=x;
20   int ka=x;
21   if(num[heap[ka]]>=num[heap[ka>>1]]){
22     int s=ka<<1;
23     while(s<=size){
24       if(s<size&&num[heap[s+1]]<num[heap[s]])s++;
25       if(num[heap[ka]]>num[heap[s]]){
26     swap(fheap[heap[ka]],fheap[heap[s]]);
27     swap(heap[ka],heap[s]);ka=s;s=ka<<1;}
28       else break;}}
29   else{while(ka>1){if(num[heap[ka]]<num[heap[ka>>1]]){
30     swap(fheap[heap[ka]],fheap[heap[ka>>1]]);
31     swap(heap[ka],heap[ka>>1]);ka>>=1;}
32       else break;}}
33 }
34 inline void insert(int x)
35 {
36   heap[++size]=x;fheap[x]=size;int ka=size;
37   while(ka>1){
38     if(num[heap[ka]]<num[heap[ka>>1]])
39       {swap(fheap[heap[ka]],fheap[heap[ka>>1]]);
40     swap(heap[ka],heap[ka>>1]);ka>>=1;}
41     else break;}
42 }
43 int main()
44 {
45   n=read();k=read();int x1,x2;
46   x1=read();Fi(i,2,n){
47     nxt[i]=i+1;pre[i]=i-1;x2=read();
48     num[i]=x2-x1;x1=x2;insert(i);}
49   num[1]=1e9+7;num[++n]=1e9+7;
50   insert(1),insert(n);
51   Fi(i,1,k){
52     int x=heap[1];delet(1);
53     delet(fheap[pre[x]]);delet(fheap[nxt[x]]);
54     int x1=num[pre[x]],x2=num[nxt[x]];
55     num[++n]=x1+x2-num[x];
56     pre[n]=pre[pre[x]];nxt[n]=nxt[nxt[x]];
57     pre[nxt[n]]=n;nxt[pre[n]]=n;insert(n);
58     ans+=num[x];}cout<<ans;return 0;
59 }

洛谷P3620 [APIO/CTSC 2007] 數據備份 [堆，貪心，差分]