若向平衡二叉樹中插入一個新結點後破壞了平衡二叉樹的平衡性。首先要找出插入新結點後失去平衡的最小子樹根結點的指針。然後再調整這個子樹中有關結點之間的鏈接關系，使之成為新的平衡子樹。當失去平衡的最小子樹被調整為平衡子樹後，原有其他所有不平衡子樹無需調整，整個二叉排序樹就又成為一棵平衡二叉樹。

失去平衡的最小子樹是指以離插入結點最近，且平衡因子絕對值大於 1 的結點作為根的子樹。假設用 A 表示失去平衡的最小子樹的根結點，則調整該子樹的操作可歸納為下列四種情況。

（ 1 ） RR 型平衡旋轉法

由於在 A 的左孩子 B 的左子樹上插入結點 F ，使 A 的平衡因子由 1 增至 2 而失去平衡。故需進行一次順時針旋轉操作。 即將 A 的左孩子 B 向右上旋轉代替 A 作為根結點， A 向右下旋轉成為 B 的右子樹的根結點。而原來 B 的右子樹則變成 A 的左子樹。

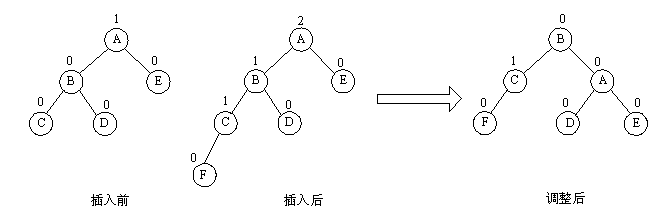
（ 2 ） LL 型平衡旋轉法

由於在 A 的右孩子 C 的右子樹上插入結點 F ，使 A 的平衡因子由 -1 減至 -2 而失去平衡。故需進行一次逆時針旋轉操作。即將 A的右孩子 C 向左上旋轉代替 A 作為根結點， A 向左下旋轉成為 C 的左子樹的根結點。而原來 C 的左子樹則變成 A 的右子樹。

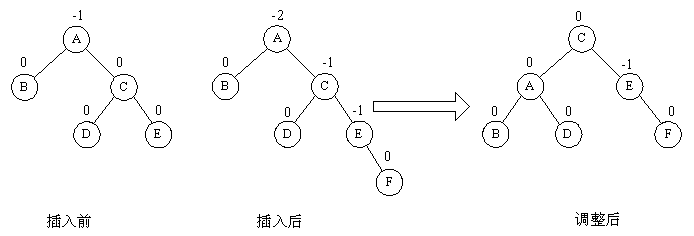
（ 3 ） LR 型平衡旋轉法

由於在 A 的左孩子 B 的右子數上插入結點 F ，使 A 的平衡因子由 1 增至 2 而失去平衡。故需進行兩次旋轉操作（先逆時針，後順時針）。即先將 A 結點的左孩子 B 的右子樹的根結點 D 向左上旋轉提升到 B 結點的位置，然後再把該 D 結點向右上旋轉提升到 A 結點的位置。即先使之成為 LL 型，再按 LL 型處理 。

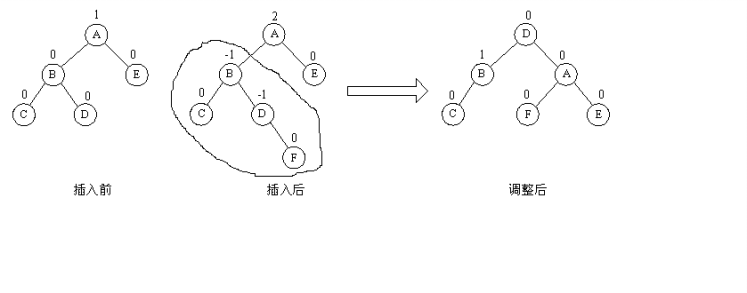
如圖中所示，即先將圓圈部分先調整為平衡樹，然後將其以根結點接到 A 的左子樹上，此時成為 LL 型，再按 LL 型處理成平衡型。

（ 4 ） RL 型平衡旋轉法

由於在 A 的右孩子 C 的左子樹上插入結點 F ，使 A 的平衡因子由 -1 減至 -2 而失去平衡。故需進行兩次旋轉操作（先順時針，後逆時針），即先將 A 結點的右孩子 C 的左子樹的根結點 D 向右上旋轉提升到 C 結點的位置，然後再把該 D 結點向左上旋轉提升到 A 結點的位置。即先使之成為 RR 型，再按 RR 型處理。

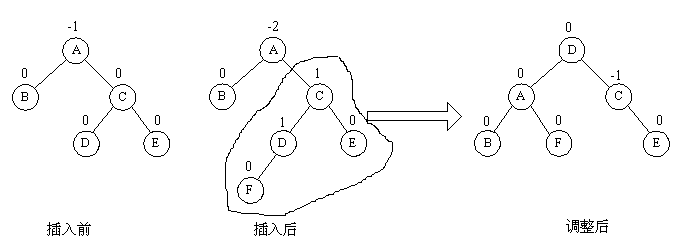
如圖中所示，即先將圓圈部分先調整為平衡樹，然後將其以根結點接到 A 的左子樹上，此時成為 RR 型，再按 RR 型處理成平衡型。

平衡化靠的是旋轉。 參與旋轉的是 3 個節點（其中一個可能是外部節點 NULL ），旋轉就是把這 3 個節點轉個位置。註意的是，左旋的時候 p->right 一定不為空，右旋的時候 p->left 一定不為空，這是顯而易見的。

如果從空樹開始建立，並時刻保持平衡，那麽不平衡只會發生在插入刪除操作上，而不平衡的標誌就是出現 bf == 2 或者 bf == -2的節點。

平衡二叉樹的循轉過程（轉載）