分步圖解平衡二叉樹的插入過程(Python實現)
一、基本概念:
平衡二叉樹:是一種特殊的二叉排序樹,它或者為空樹,或者每個結點的左右子樹都是平衡二叉樹,也就是每個結點的左右子樹的高度之差只能是-1,0,1三種情況。
平衡二叉樹又稱AVL樹,是由蘇聯的Georgy Adelson-Velsky和E.M.Landis發明的,並以他們的名字命名。與之類似的還有紅黑樹、B樹等。
平衡二叉樹的平衡狀況由平衡因子(Balance Factor,BF)來衡量。平衡因子定義為當前結點的左子樹高度減去右子樹的高度之差,其可能取值只有-1,0,1。葉結點的BF都是0。如果能維持平衡二叉樹的結構,檢索操作就能在O(log n)時間內完成。
最小不平衡子樹:距離插入結點最近的,且平衡因子的絕對值大於1的結點為根的子樹。(不平衡即失衡,指BF超出合法值)
最小非平衡子樹:包含插入結點位置,其根結點的BF是1或-1的最小子樹。(非平衡指BF非0,但BF在合法值範圍內)
(此處這兩個概念如有錯誤,歡迎指正)
在下圖中,原來結點4的BF=1,插入結點3後,結點4的BF=2。結點4是距離插入結點3最近的且BF絕對值大於1的結點,所以以結點4為根的子樹就是最小不平衡子樹。
二、插入操作的不同情況
1、如果在查詢插入位置的過程中,所有途經結點的BF值均為0,那麼插入新的結點後,不會導致這些途經結點失衡,只會讓它們的BF值從0變為1或者-1。
如下圖所示,插入結點3,查詢時途經結點為5,4和2,其BF只是從原來的0都變為了1或-1,整棵樹仍然是平衡的。
2、如下圖,插入結點4.7。左圖中最小非平衡子樹以結點4為根結點a,結點4.7被插入到這棵子樹較低的子樹中,此時這棵子樹還是平衡的,只需要修改這棵子樹的從根結點直至插入結點路徑上所有結點的BF值。
以上兩種情況都不需要調整樹的結構
3、需要調整樹結構的情況又分為了四種情況:
(1)LL型調整:a的左子樹較高,新結點插入在a的左子樹的左子樹。進行右旋轉。
在下圖的圖a中,a是最小非平衡子樹的根,b的BF一定是0(否則a就不是最小非平衡子樹的根了)。結點2被插入到了a的左子樹的左子樹,需要進行LL型調整:將結點2-3-4-5-8看做一條可以轉動的鏈子,將其向右旋轉(順時針)一個結點,然後將原來b結點的右子樹,接到a結點的左子結點上,調整完成。
再說明一下插入結點的位置:插入結點不必像上圖一樣,必須插在某個結點的左子結點,也可以像下圖一樣,插在某個結點的右子結點,調整的方法還是一樣的。這也是定義中說:新結點插入在a的左子樹的‘左子樹’,而不是左子樹的左子結點的原因。
@staticmethod
def LL(a, b):
a.left = b.right # 將b的右子樹接到a的左子結點上
b.right = a #將a樹接到b的右子結點上
a.bf = b.bf = 0 #調整a、b的bf值。
return b(2)RR型調整:a的右子樹較高,新結點插入在a的右子樹的右子樹。進行左旋轉。
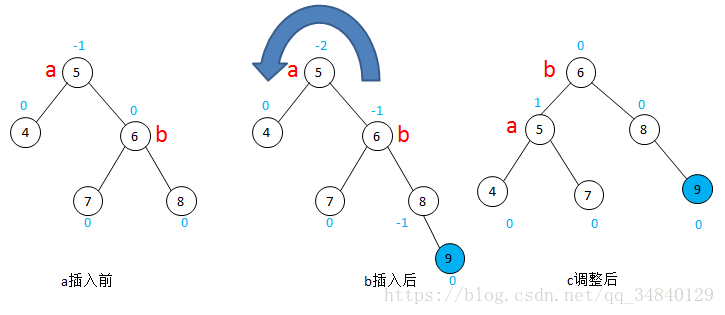
RR型調整與LL型正好是對稱的,操作步驟類似。在下圖的圖a中,a是最小非平衡子樹的根,b的BF一定是0。結點9被插入到了a的右子樹的右子樹,需要進行RR型調整:同樣地,將結點4-5-6-8-9看做一條可以轉動的鏈子,將其向左旋轉(逆時針)一個結點,然後將原來b結點的左子樹,接到a結點的右子結點上,調整完成。
同樣地,插入結點也可以插入在結點8的左子結點處,調整步驟是一樣的。
@staticmethod
def RR(a, b):
a.right = b.left
b.left = a
a.bf = b.bf = 0
return b(3)LR型調整:a的左子樹較高,新結點插入在a的左子樹的右子樹。先進行左旋轉,再進行右旋轉。
在下圖的圖a中,a是最小非平衡子樹的根,b的BF一定是0,c的BF也一定是0。結點4.1被插入到了a的左子樹的右子樹(圖b中4.1插入到了c結點的左子樹,當然也可以插到c結點的右子樹,其調整過程都是一樣的),需要進行LR型調整。
圖c中,首先將c結點的左右子樹分別摘下來,然後將結點4.5-4-3-2看做一條可以轉動的鏈子,對其進行左旋轉(逆時針)一個結點,就得到了圖d,然後再將結點2-3-4-4.5-5-8-9看做一條轉動的鏈子,將其進行右旋轉(順時針)一個結點,就得到了圖e。
最後將原來c結點的左子樹接到b結點的右子結點上,將原來c結點的右子樹接到a結點的左子結點上,調整完成。
@staticmethod
def LR(a,b):
c = b.right
a.left, b.right = c.right, c.left
c.left, c.right = b, a
if c.bf == 0: #c本身就是插入點
a.bf = b.bf = 0
elif c.bf == 1: #插在c的左子樹
a.bf = -1
b.bf = 0
else: #插在c的右子樹
a.bf = 0
b.bf = 1
c.bf = 0
return c(4)RL型調整:a的右子樹較高,新結點插入在a的右子樹的左子樹。先進行右旋轉,再進行左旋轉。
RL型調整與LR型正好是對稱的,操作步驟類似。在下圖的圖a中,a是最小非平衡子樹的根,b的BF一定是0,c的BF也一定是0。結點5.5被插入到了a的右子樹的左子樹(圖b中5.5插入到了c結點的左子樹,當然也可以插到c結點的右子樹,其調整過程都是一樣的),需要進行RL型調整。
圖c中,首先將c結點的左右子樹分別摘下來,然後將結點7-9-10-11看做一條可以轉動的鏈子,對其進行右旋轉(順時針)一個結點,就得到了圖d,然後再將結點3-4-5-7-9-10-11看做一條轉動的鏈子,將其進行左旋轉(逆時針)一個結點,就得到了圖e。
最後將原來c結點的左子樹接到a結點的右子結點上,將原來c結點的右子樹接到b結點的左子結點上,調整完成。
@staticmethod
def RL(a, b):
c = b.left
a.right, b.left = c.left, c.right
c.left, c.right = a, b
if c.bf == 0:
a.bf = b.bf = 0
elif c.bf == 1:
a.bf = 0
b.bf = -1
else:
a.bf = 1
b.bf = 0
c.bf = 0
return c平衡二叉樹的插入操作的複雜度是O(log n)
最後:用平衡二叉樹來實現一個字典類
首先,AVL樹結點類需要增加一個bf域。
class AVLNode(BinTNode):
def __init__(self, data):
BinTNode.___init__(self,data)
self.bf = 0其次,AVL數是一種二叉排序樹,所以可以直接繼承二叉排序樹的方法。
class DictAVL(DictBinTree):
def __init__(self, data):
DictBinTree.___init__(self)插入操作的實現:
def insert(self, key, value):
a = p = self.root
if a is None: #如果根結點為空,則直接將值插入到根結點
self.root = AVLNode(Assoc(key, value))
return
a_father, p_father = None #a_father用於最後將調整後的子樹接到其子結點上
while p is not None: #通過不斷的迴圈,將p下移,查詢插入位置,和最小非平衡子樹
if key == p.data.key: #如果key已經存在,則直接修改其關聯值
p.data.value = value
return
if p.bf != 0: #如果當前p結點的BF=0,則有可能是最小非平衡子樹的根結點
a_father, a, = p_father, p
p_father = p
if key < p.data.key:
p = p.left
else:
p = p.right
#上述迴圈結束後,p_father已經是插入點的父結點,a_father和a記錄著最小非平衡子樹
node = AVLNode(Assoc(key, value))
if key < p_father.data.key:
p_father.left = node
else:
p_father.right = node
#新結點已插入,a是最小非平衡子樹的根結點
if key < a.data.key: #新結點在a的左子樹
p = b = a.left
d = 1 #d記錄新結點被 插入到a的哪棵子樹
else:
p = b = a.right #新結點在a的右子樹
d = -1
#在新結點插入後,修改b到新結點路徑上各結點的BF值。調整過程的BF值修改都在子函式中操作
while p != node:
if key < p.data.key:
p.bf = 1
p = p.left
else:
p.bf = -1
p = p.right
if a.bf == 0: #如果a的BF原來為0,那麼插入新結點後不會失衡
a.bf = d
return
if a.bf == -d: #如果新結點插入在a較低的子樹裡
a.bf = 0
return
#以上兩條if語句都不符合的話,說明新結點被插入在較高的子樹裡,需要進行調整
if d == 1: #如果新結點插入在a的左子樹
if b.bf == 1: #b的BF原來為0,如果等於1,說明新結點插入在b的左子樹
b = DictAVL.LL(a, b)
else: #新結點插入在b的右子樹
b = DictAVL.LR(a, b)
else: #新結點插入在a的右子樹
if b.bf == -1: #新結點插入在b的右子樹
b = DictAVL.RR(a, b)
else: ##新結點插入在b的左子樹
b = DictAVL.RL(a, b)
#將調整後的最小非平衡子樹接到原樹中,也就是接到原來a結點的父結點上
if a_father is None: #判斷a是否是根結點
self.root = b
else:
if a_father == a:
a_father.left = b
else:
a_father.right = b完整的程式碼如下:
class StackUnderflow(ValueError):
pass
class SStack():
def __init__(self):
self.elems = []
def is_empty(self):
return self.elems == []
def top(self): #取得棧裡最後壓入的元素,但不刪除
if self.elems == []:
raise StackUnderflow('in SStack.top()')
return self.elems[-1]
def push(self, elem):
self.elems.append(elem)
def pop(self):
if self.elems == []:
raise StackUnderflow('in SStack.pop()')
return self.elems.pop()
class Assoc: #定義一個關聯類
def __init__(self, key, value):
self.key = key #鍵(關鍵碼)
self.value = value #值
def __lt__(self, other):#Python直譯器中遇到比較運算子<,會去找類裡定義的__lt__方法(less than)
return self.key < other.key
def __le__(self, other): #(less than or equal to)
return self.key < other.key or self.key == other.key
def __str__(self):
return 'Assoc({0},{1})'.format(self.key, self.value) #key和value分別替換前面{0},{1}的位置。
class BinTNode:
def __init__(self, dat, left = None, right = None):
self.data = dat
self.left = left
self.right = right
class DictBinTree:
def __init__(self, root = None):
self.root = root
def is_empty(self):
return self.root is None
def search(self, key):#檢索是否存在關鍵碼key
bt = self.root
while bt is not None:
entry = bt.data
if key < entry.key:
bt = bt.left
elif key > entry.key:
bt = bt.right
else:
return entry.value
return None
def insert(self, key, value):
bt = self.root
if bt is None:
self.root = BinTNode(Assoc(key, value))
return
while True:
entry = bt.data
if key < entry.key: #如果小於當前關鍵碼,轉向左子樹
if bt.left is None: #如果左子樹為空,就直接將資料插在這裡
bt.left = BinTNode(Assoc(key,value))
return
bt = bt.left
elif key > entry.key:
if bt.right is None:
bt.right = BinTNode(Assoc(key,value))
return
bt = bt.right
else:
bt.data.value = value
return
def print_all_values(self):
bt, s = self.root, SStack()
while bt is not None or not s.is_empty(): #最開始時棧為空,但bt不為空;bt = bt.right可能為空,棧不為空;當兩者都為空時,說明已經全部遍歷完成了
while bt is not None:
s.push(bt)
bt = bt.left
bt = s.pop() #將棧頂元素彈出
yield bt.data.key, bt.data.value
bt = bt.right #將當前結點的右子結點賦給bt,讓其在while中繼續壓入棧內
def entries(self):
bt, s = self.root, SStack()
while bt is not None or not s.is_empty():
while bt is not None:
s.push(bt)
bt = bt.left
bt = s.pop()
yield bt.data.key, bt.data.value
bt = bt.right
def print_key_value(self):
for k, v in self.entries():
print(k, v)
def delete(self, key):
#以下這一段用於找到待刪除結點及其父結點的位置。
del_position_father, del_position = None, self.root #del_position_father是待刪除結點del_position的父結點
while del_position is not None and del_position.data.key != key: #通過不斷的比較,找到待刪除結點的位置
del_position_father = del_position
if key < del_position.data.key:
del_position = del_position.left
else:
del_position = del_position.right
if del_position is None:
print('There is no key')
return
if del_position.left is None: #如果待刪除結點只有右子樹
if del_position_father is None: #如果待刪除結點的父結點是空,則說明待刪除結點是根結點
self.root = del_position.right #則直接將根結點置空
elif del_position is del_position_father.left: #如果待刪除結點是其父結點的左結點
del_position_father.left = del_position.right #***改變待刪除結點父結點的左子樹的指向
else:
del_position_father.right = del_position.right
return
#如果既有左子樹又有右子樹,或者僅有左子樹時,都可以用直接前驅替換的刪除結點的方式,只不過得到的二叉樹與原理中說明的不一樣,但是都滿足要求。
pre_node_father, pre_node = del_position, del_position.left
while pre_node.right is not None: #找到待刪除結點的左子樹的最右結點,即為待刪除結點的直接前驅
pre_node_father = pre_node
pre_node = pre_node.right
del_position.data = pre_node.data #將前驅結點的data賦給刪除結點即可,不需要改變其原來的連線方式
if pre_node_father.left is pre_node:
pre_node_father.left = pre_node.left
if pre_node_father.right is pre_node:
pre_node_father.right = pre_node.left
def build_dictBinTree(entries):
dic = DictBinTree()
for k,v in entries:
dic.insert(k,v)
return dic
class AVLNode(BinTNode):
def __init__(self, data):
BinTNode.___init__(self,data)
self.bf = 0
class DictAVL(DictBinTree):
def __init__(self, data):
DictBinTree.___init__(self)
@staticmethod
def LL(a, b):
a.left = b.right # 將b的右子樹接到a的左子結點上
b.right = a #將a樹接到b的右子結點上
a.bf = b.bf = 0 #調整a、b的bf值。
return b
@staticmethod
def RR(a, b):
a.right = b.left
b.left = a
a.bf = b.bf = 0
return b
@staticmethod
def LR(a,b):
c = b.right
a.left, b.right = c.right, c.left
c.left, c.right = b, a
if c.bf == 0: #c本身就是插入點
a.bf = b.bf = 0
elif c.bf == 1: #插在c的左子樹
a.bf = -1
b.bf = 0
else: #插在c的右子樹
a.bf = 0
b.bf = 1
c.bf = 0
return c
@staticmethod
def RL(a, b):
c = b.left
a.right, b.left = c.left, c.right
c.left, c.right = a, b
if c.bf == 0:
a.bf = b.bf = 0
elif c.bf == 1:
a.bf = 0
b.bf = -1
else:
a.bf = 1
b.bf = 0
c.bf = 0
return c
def insert(self, key, value):
a = p = self.root
if a is None: #如果根結點為空,則直接將值插入到根結點
self.root = AVLNode(Assoc(key, value))
return
a_father, p_father = None #a_father用於最後將調整後的子樹接到其子結點上
while p is not None: #通過不斷的迴圈,將p下移,查詢插入位置,和最小非平衡子樹
if key == p.data.key: #如果key已經存在,則直接修改其關聯值
p.data.value = value
return
if p.bf != 0: #如果當前p結點的BF=0,則有可能是最小非平衡子樹的根結點
a_father, a, = p_father, p
p_father = p
if key < p.data.key:
p = p.left
else:
p = p.right
#上述迴圈結束後,p_father已經是插入點的父結點,a_father和a記錄著最小非平衡子樹
node = AVLNode(Assoc(key, value))
if key < p_father.data.key:
p_father.left = node
else:
p_father.right = node
#新結點已插入,a是最小非平衡子樹的根結點
if key < a.data.key: #新結點在a的左子樹
p = b = a.left
d = 1 #d記錄新結點被 插入到a的哪棵子樹
else:
p = b = a.right #新結點在a的右子樹
d = -1
#在新結點插入後,修改b到新結點路徑上各結點的BF值。調整過程的BF值修改都在子函式中操作
while p != node:
if key < p.data.key:
p.bf = 1
p = p.left
else:
p.bf = -1
p = p.right
if a.bf == 0: #如果a的BF原來為0,那麼插入新結點後不會失衡
a.bf = d
return
if a.bf == -d: #如果新結點插入在a較低的子樹裡
a.bf = 0
return
#以上兩條if語句都不符合的話,說明新結點被插入在較高的子樹裡,需要進行調整
if d == 1: #如果新結點插入在a的左子樹
if b.bf == 1: #b的BF原來為0,如果等於1,說明新結點插入在b的左子樹
b = DictAVL.LL(a, b)
else: #新結點插入在b的右子樹
b = DictAVL.LR(a, b)
else: #新結點插入在a的右子樹
if b.bf == -1: #新結點插入在b的右子樹
b = DictAVL.RR(a, b)
else: ##新結點插入在b的左子樹
b = DictAVL.RL(a, b)
#將調整後的最小非平衡子樹接到原樹中,也就是接到原來a結點的父結點上
if a_father is None: #判斷a是否是根結點
self.root = b
else:
if a_father == a:
a_father.left = b
else:
a_father.right = b
if __name__=="__main__":
#LL調整
entries = [(5,'a'),(2.5,'g'),(2.3,'h'),(3,'b'),(2,'d'),(4,'e'),(3.5,'f')]
dic = build_dictBinTree(entries)
dic.print_key_value()
print('after inserting')
dic.insert(1, 'i')
dic.print_key_value()
#LR調整
entries = [(2.5,'g'),(3,'b'),(4,'e'),(3.5,'f')]
dic = build_dictBinTree(entries)
dic.print_key_value()
print('after inserting')
dic.insert(3.2, 'i') #LL
dic.print_key_value()