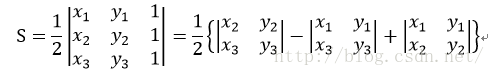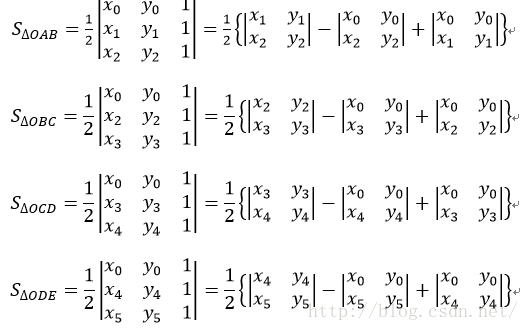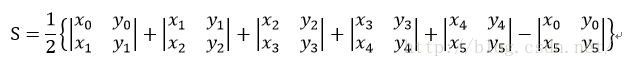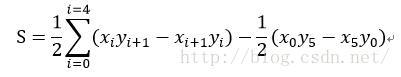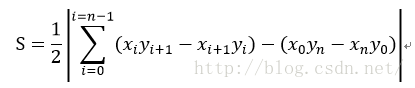任意給出一個三角形ΔABC，設其頂點坐標分別為A（x1, y1），B（x2, y2），C（x3, y3），那麽根據線性代數的知識，ΔABC的有向面積可表示為：

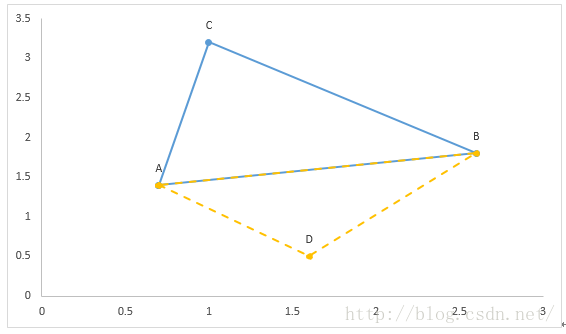
其中，ΔABC頂點A、B、C逆時針給出時有向面積為正，順時針給出時有向面積為負。如圖1所示，S?ABC>0、S?ABD<0.

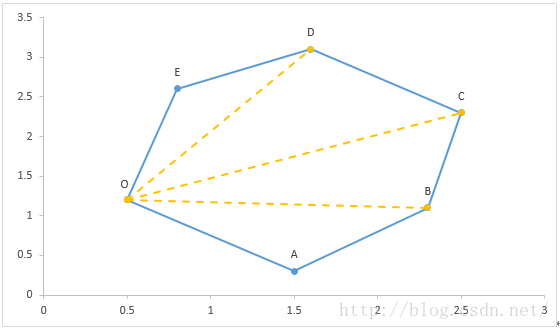
我們知道任意的多邊形都可以分割成多個三角形，根據以上三角形面積公式就可以求出任意多邊形的面積。如圖2所示的六邊形頂點坐標分別為O（x0, y0），A（x1, y1），B（x2, y2），C（x3, y3），D（x4, y4），E（x5, y5），則其面積可以表示為四個三角形面積之和：S=S?OAB+S?OBC+S?OCD+S?ODE

其中：

所以

即

圖2

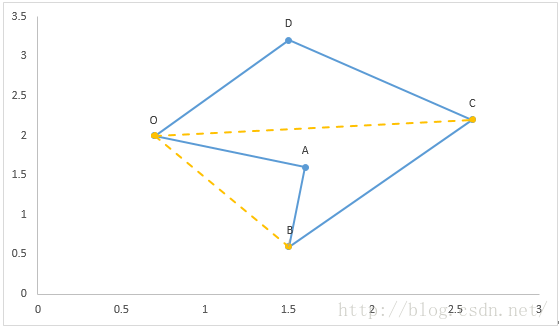
在這裏，前文給出的多邊形示例是一個凸多邊形，那麽這一結論適用於凹多邊形嗎？下面我們看看如圖3所示的凹多邊形。

按照上面的思路，這裏的凹多邊形面積表示為：S=S?OAB+S?OBC+S?OCD，從前面介紹可以知道

S?OAB=-S?OBA<0，所以很明顯上式是成立的，即此公式也適用於凹多邊形。

經過以上分析，給出任意一個多邊形，其頂點坐標依次為（x0，y0），（x1，y1），（x2，y2），...，（xn，yn）（其中n=2，3，4，…），則其面積可表示為：

換句話說，若已知多邊形邊上的每一點坐標，我們就可以求出該多邊形的面積，包括如圖4所示的曲線圖形，當從O點到A點到O點的曲線上每一點坐標都已知時就能求出該曲線圖的面積。

多邊形面積