時間序列模式(ARIMA)---Python實現
時間序列分析的主要目的是根據已有的歷史數據對未來進行預測。如餐飲銷售預測可以看做是基於時間序列的短期數據預測, 預測的對象時具體菜品的銷售量。
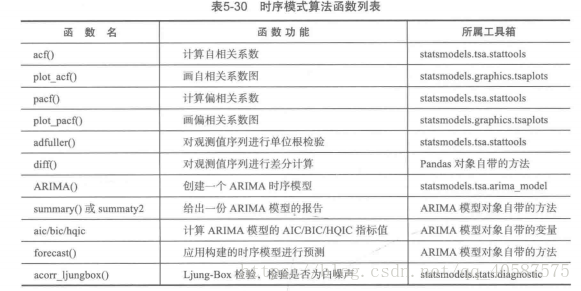
1.時間序列算法:
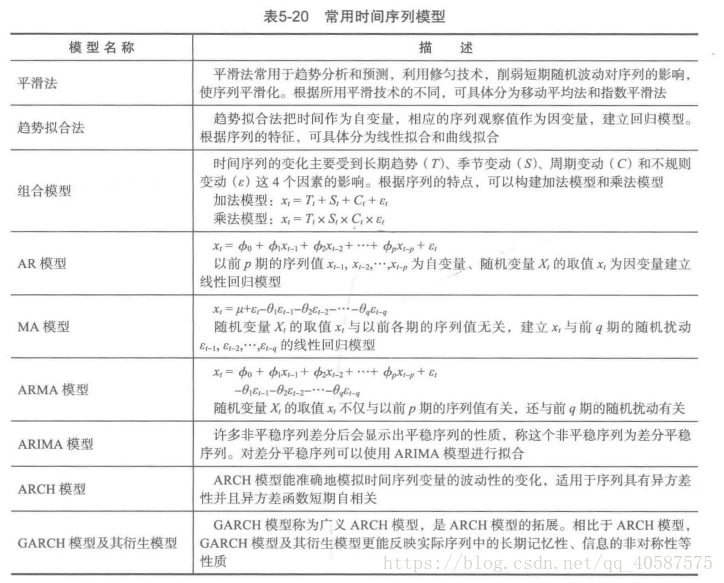
常見的時間序列模型;
2.時序模型的預處理
1. 對於純隨機序列,也稱為白噪聲序列,序列的各項之間沒有任何的關系, 序列在進行完全無序的隨機波動, 可以終止對該序列的分析。
2. 對於平穩非白噪聲序列, 它的均值和方差是常數。ARMA 模型是最常用的平穩序列擬合模型。
3. 對於非平穩序列, 由於它的方差和均值不穩定, 處理方法一般是將其轉化成平穩序列。 可以使用ARIMA 模型進行分析。
對平穩性的檢驗:
1.時序圖檢驗:根據平穩時間序列的均值和方差都是常數的特性,平穩序列的時序圖顯示該序列值時鐘在一個參數附近隨機波動,而且波動的範圍是有界的。
2.自相關圖檢驗:平穩序列具有短期相關性, 這個性質表明對平穩序列而言, 通常 只有近期的序列值得影響比較明顯, 間隔越遠的過去值對現在的值得影響越小。 而非平穩序列的自相關系數衰減的速度比較慢。
3.單位根檢驗:單位根檢驗是指檢驗序列中是否存在單位根, 如果存在單位根, 那就是非平穩時間序列。 目前最常用的方法就是單位根檢驗。
原假設是 非平穩序列過程, 備擇假設是 平穩序列, 趨勢平穩過程
上述參考:百度文庫
3.時間序列分析:
?平穩性:
?平穩性要求經由樣本時間序列所得到的擬合曲線,在未來一段時間內仍然沿著現有的形態‘慣性’地延續下去。
?平穩性要求序列的均值和方差不發生明顯的變化。
?弱平穩:期望和相關系數(依賴性)不變,未來某個時刻t 的值,Xt 要依賴於它過去的信息。
?差分法:時間序列在 T 與 T-1 時刻的差值(使用差分使其滿足平穩性),一般差分1,2 階就可以了。
?AR(自回歸模型):
?描述當前值與歷史值之間的關系, 用變量自身的歷史時間數據對自身進行預測。自回歸模型必須滿足平穩性的要求。
公式定義:
自回歸模型的限制:
1.自回歸模型是使用自身的數據進行預測的
2.必須具有平穩性
3.必須具有相關性,如果相關性小於 0.5 , 則不宜使用
4.自回歸模型只適用於預測與自身前期相關的預測。
?MA(移動平均模型):
?移動平均模型關註的是自回歸模型中的誤差項的累加
?移動平均法能有效地消除預測中的隨機波動。
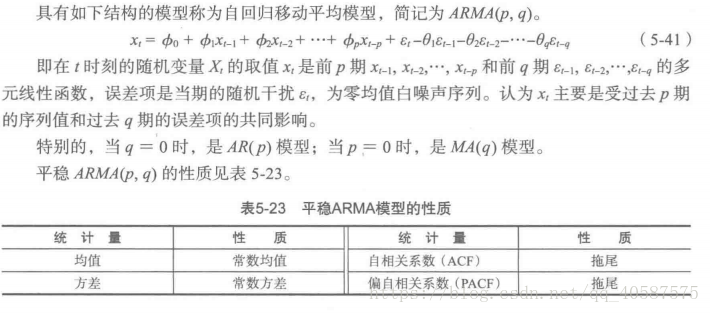
?ARMA(自回歸平均模型):
?自回歸和移動平均的結合。
?ARIMA(p,d,q)差分自回歸移動平均模型(Autoregressive Integrated Moving Average Model ,簡稱ARIMA)
?AR 是自回歸, p 是自回歸項, MA 是移動平均, q 為移動平均項, d 為時間序列稱為平穩時 所做的差分次數。
?原理: 將非平穩時間序列轉換成平穩時間序列, 然後將因變量僅對它的滯後值(p階)以及隨機誤差項的現值和滯後值進行回顧所建立的模型。
?ARIMA 建模流程:
?1.將序列平穩化(差分法確定 d)
?2.p 和 q 階數的確定(ACF 和 PACF 確定)
?3.建立模型 ARIMA (p , d , q )
使用ARIMA 模型對某餐廳的銷售數據進行預測
#使用ARIMA 模型對非平穩時間序列進行建模操作
#差分運算具有強大的確定性的信息提取能力, 許多非平穩的序列差分後顯示出平穩序列的性質, 這是稱這個非平穩序列為差分平穩序列。
#對差分平穩序列可以還是要ARMA 模型進行擬合, ARIMA 模型的實質就是差分預算與 ARMA 模型的結合。
#coding=gbk
#使用ARIMA 模型對非平穩時間序列記性建模操作
#差分運算具有強大的確定性的信息提取能力, 許多非平穩的序列差分後顯示出平穩序列的性質, 這是稱這個非平穩序列為差分平穩序列。
#對差分平穩序列可以還是要ARMA 模型進行擬合, ARIMA 模型的實質就是差分預算與 ARMA 模型的結合。
#導入數據
import pandas as pd
filename = r‘D:\datasets\arima_data.xls‘
data = pd.read_excel(filename, index_col = u‘日期‘)
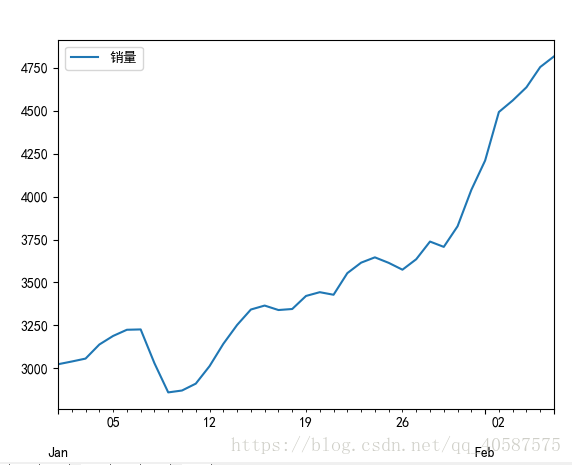
#畫出時序圖
import matplotlib.pyplot as plt
plt.rcParams[‘font.sans-serif‘] = [‘SimHei‘] #定義使其正常顯示中文字體黑體
plt.rcParams[‘axes.unicode_minus‘] = False #用來正常顯示表示負號
# data.plot()
# plt.show()
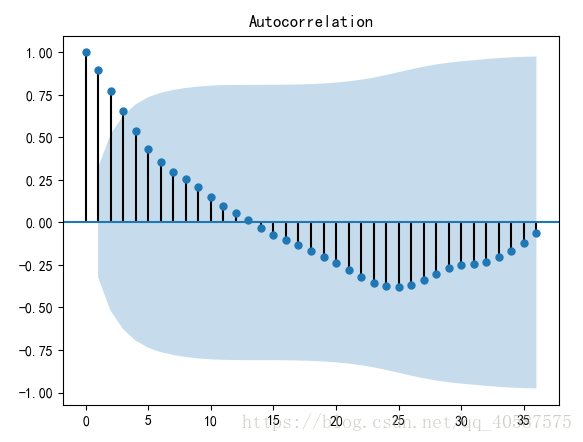
#畫出自相關性圖
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
# plot_acf(data)
# plt.show()
#平穩性檢測
from statsmodels.tsa.stattools import adfuller
print(‘原始序列的檢驗結果為:‘,adfuller(data[u‘銷量‘]))
#原始序列的檢驗結果為: (1.8137710150945268, 0.9983759421514264, 10, 26, {‘1%‘: -3.7112123008648155,
# ‘10%‘: -2.6300945562130176, ‘5%‘: -2.981246804733728}, 299.46989866024177)
#返回值依次為:adf, pvalue p值, usedlag, nobs, critical values臨界值 , icbest, regresults, resstore
#adf 分別大於3中不同檢驗水平的3個臨界值,單位檢測統計量對應的p 值顯著大於 0.05 , 說明序列可以判定為 非平穩序列
#對數據進行差分後得到 自相關圖和 偏相關圖
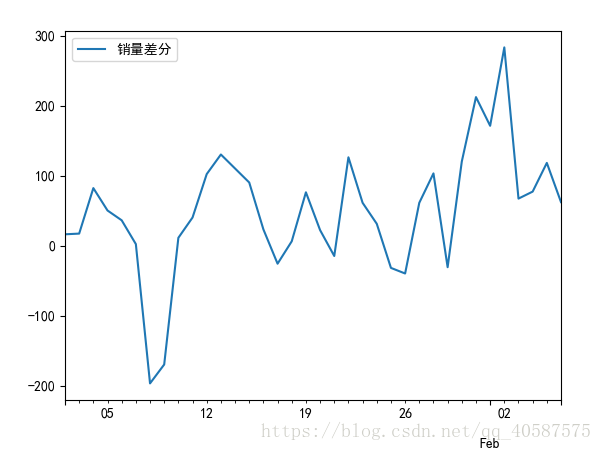
D_data = data.diff().dropna()
D_data.columns = [u‘銷量差分‘]
D_data.plot() #畫出差分後的時序圖
# plt.show()
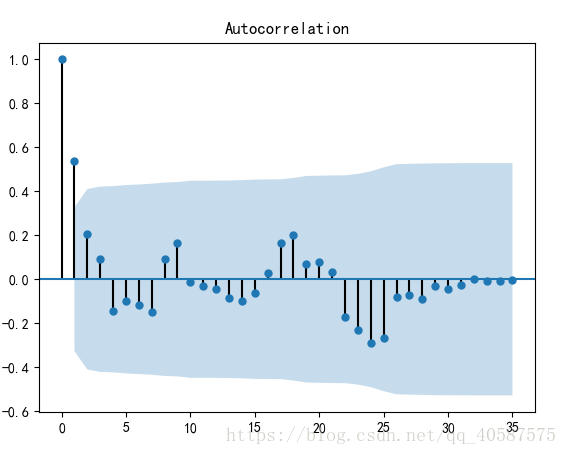
plot_acf(D_data) #畫出自相關圖
# plt.show()
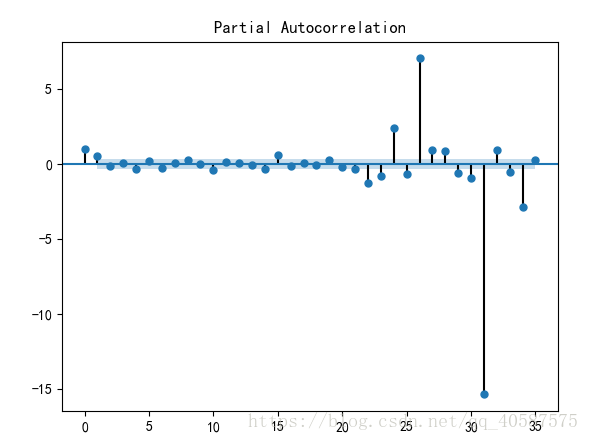
plot_pacf(D_data) #畫出偏相關圖
# plt.show()
print(u‘差分序列的ADF 檢驗結果為: ‘, adfuller(D_data[u‘銷量差分‘])) #平穩性檢驗
#差分序列的ADF 檢驗結果為: (-3.1560562366723537, 0.022673435440048798, 0, 35, {‘1%‘: -3.6327426647230316,
# ‘10%‘: -2.6130173469387756, ‘5%‘: -2.9485102040816327}, 287.5909090780334)
#一階差分後的序列的時序圖在均值附近比較平穩的波動, 自相關性有很強的短期相關性, 單位根檢驗 p值小於 0.05 ,所以說一階差分後的序列是平穩序列
#對一階差分後的序列做白噪聲檢驗
from statsmodels.stats.diagnostic import acorr_ljungbox
print(u‘差分序列的白噪聲檢驗結果:‘,acorr_ljungbox(D_data, lags= 1)) #返回統計量和 p 值
# 差分序列的白噪聲檢驗結果: (array([11.30402222]), array([0.00077339])) p值為第二項, 遠小於 0.05
#對模型進行定階
from statsmodels.tsa.arima_model import ARIMA
pmax = int(len(D_data) / 10) #一般階數不超過 length /10
qmax = int(len(D_data) / 10)
bic_matrix = []
for p in range(pmax +1):
temp= []
for q in range(qmax+1):
try:
temp.append(ARIMA(data, (p, 1, q)).fit().bic)
except:
temp.append(None)
bic_matrix.append(temp)
bic_matrix = pd.DataFrame(bic_matrix) #將其轉換成Dataframe 數據結構
p,q = bic_matrix.stack().idxmin() #先使用stack 展平, 然後使用 idxmin 找出最小值的位置
print(u‘BIC 最小的p值 和 q 值:%s,%s‘ %(p,q)) # BIC 最小的p值 和 q 值:0,1
#所以可以建立ARIMA 模型,ARIMA(0,1,1)
model = ARIMA(data, (p,1,q)).fit()
model.summary2() #生成一份模型報告
model.forecast(5) #為未來5天進行預測, 返回預測結果, 標準誤差, 和置信區間利用模型向前預測的時期越長, 預測的誤差就會越大,這是時間預測的典型特點。
時間序列模式(ARIMA)---Python實現