【前言：本文所討論的紅黑樹之目的在於使讀者能更簡單清晰地了解紅黑樹的構造，使讀者能在紙上清晰快速地畫出紅黑樹，而不是為了寫出紅黑樹的實現代碼。

若是要在代碼級理解紅黑樹，則勢必需要記住其復雜的插入和旋轉的各種情況，我認為那只有助於增加大家對紅黑樹的恐懼，實際面試和工作中幾乎不會遇到需要自己動手實現紅黑樹的情況(很多語言的標準庫中就有紅黑樹的實現)。】

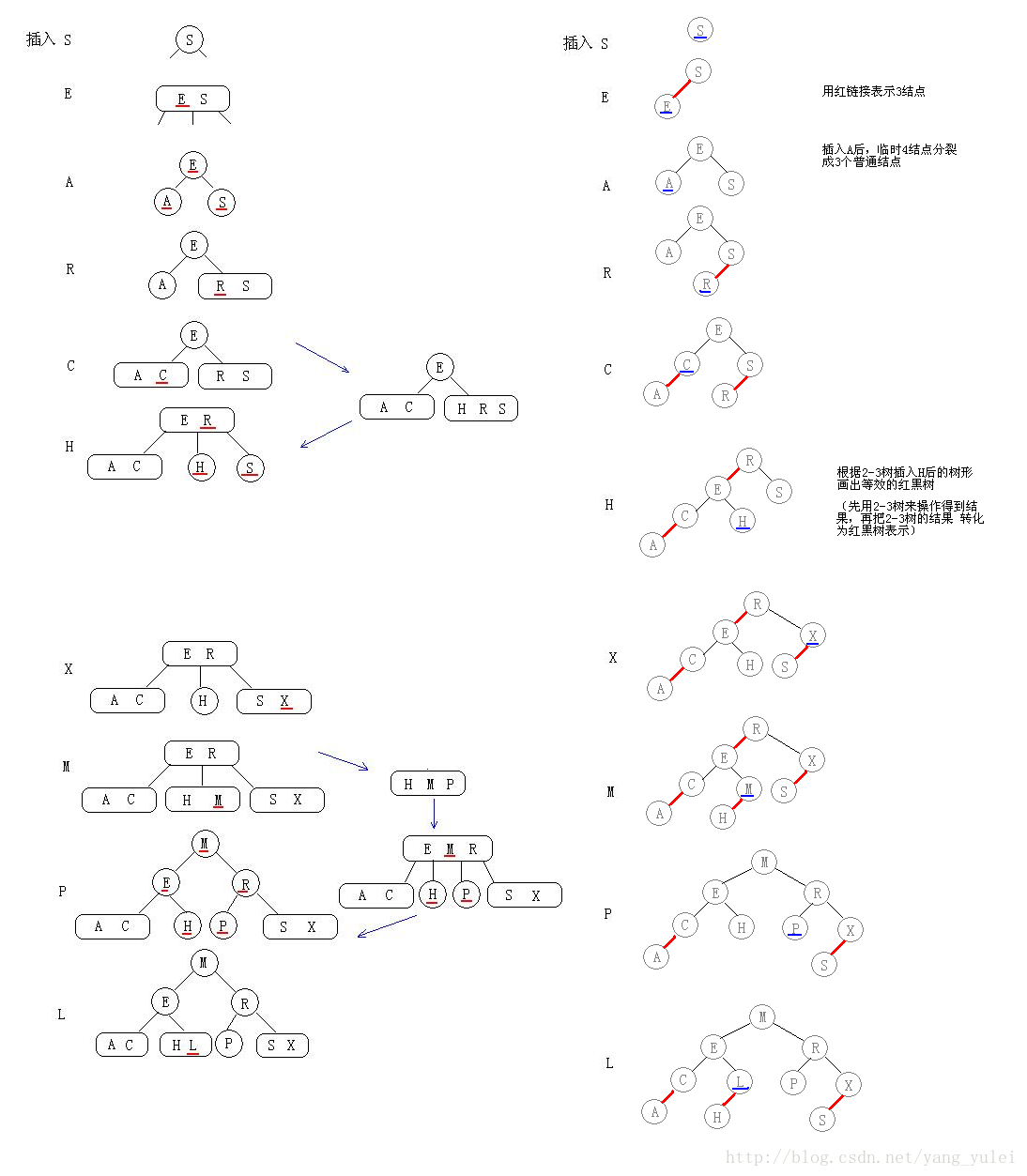
（理解紅黑樹一句話就夠了：紅黑樹就是用紅鏈接表示3-結點的2-3樹。那麽紅黑樹的插入、構造就可轉化為2-3樹的問題，即：在腦中用2-3樹來操作，得到結果，再把結果中的3-結點轉化為紅鏈接即可。而2-3樹的插入，前面已有詳細圖文，實際也很簡單：有空則插，沒空硬插，再分裂。 這樣，我們就不用記那麽復雜且讓人頭疼的紅黑樹插入旋轉的各種情況了。只要清楚2-3樹的插入方式即可。 下面圖文詳細演示。）

紅黑樹的本質：

紅黑樹是對2-3查找樹的改進，它能用一種統一的方式完成所有變換。

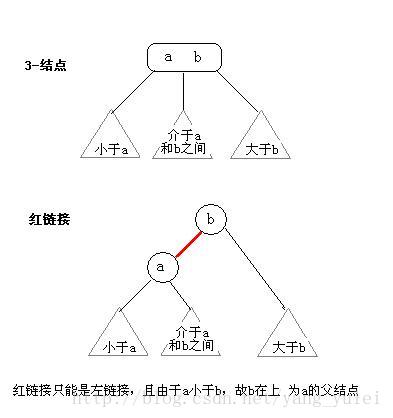
替換3-結點

★紅黑樹背後的思想是用標準的二叉查找樹（完全由2-結點構成）和一些額外的信息（替換3-結點）來表示2-3樹。

我們將樹中的鏈接分為兩種類型：紅鏈接將兩個2-結點連接起來構成一個3-結點，黑鏈接則是2-3樹中的普通鏈接。確切地說，我們將3-結點表示為由一條左斜的紅色鏈接相連的兩個2-結點。

這種表示法的一個優點是，我們無需修改就可以直接使用標準二叉查找樹的get()方法。對於任意的2-3樹，只要對結點進行轉換，我們都可以立即派生出一顆對應的二叉查找樹。我們將用這種方式表示2-3樹的二叉查找樹稱為紅黑樹。

紅黑樹的另一種定義是滿足下列條件的二叉查找樹：

⑴紅鏈接均為左鏈接。

⑵沒有任何一個結點同時和兩條紅鏈接相連。

⑶該樹是完美黑色平衡的，即任意空鏈接到根結點的路徑上的黑鏈接數量相同。

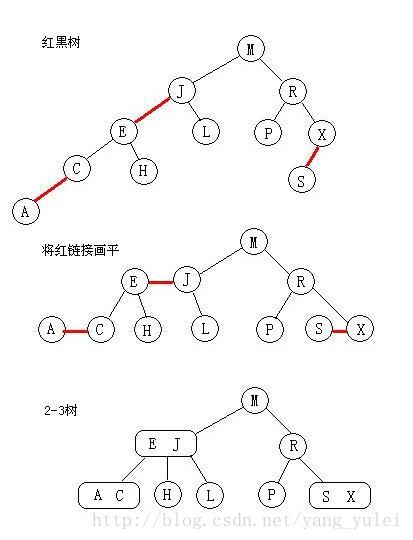
如果我們將一顆紅黑樹中的紅鏈接畫平，那麽所有的空鏈接到根結點的距離都將是相同的。如果我們將由紅鏈接相連的結點合並，得到的就是一顆2-3樹。

相反，如果將一顆2-3樹中的3-結點畫作由紅色左鏈接相連的兩個2-結點，那麽不會存在能夠和兩條紅鏈接相連的結點，且樹必然是完美平衡的。

無論我們用何種方式去定義它們，紅黑樹都既是二叉查找樹，也是2-3樹。

（2-3樹的深度很小，平衡性好，效率高，但是其有兩種不同的結點，實際代碼實現比較復雜。而紅黑樹用紅鏈接表示2-3樹中另類的3-結點，統一了樹中的結點類型，使代碼實現簡單化，又不破壞其高效性。）

顏色表示：

因為每個結點都只會有一條指向自己的鏈接（從它的父結點指向它），我們將鏈接的顏色保存在表示結點的Node數據類型的布爾變量color中（若指向它的鏈接是紅色的，那麽該變量為true，黑色則為false）。

當我們提到一個結點顏色時，我們指的是指向該結點的鏈接的顏色。

旋轉

在我們實現的某些操作中可能會出現紅色右鏈接或者兩條連續的紅鏈接，但在操作完成前這些情況都會被小心地旋轉並修復。

（我們在這裏不討論旋轉的幾種情況，把紅黑樹看做2-3樹，自然可以得到正確的旋轉後結果）

插入

在插入時我們可以使用旋轉操作幫助我們保證2-3樹和紅黑樹之間的一一對應關系，因為旋轉操作可以保持紅黑樹的兩個重要性質：有序性和完美平衡性。

熱身：

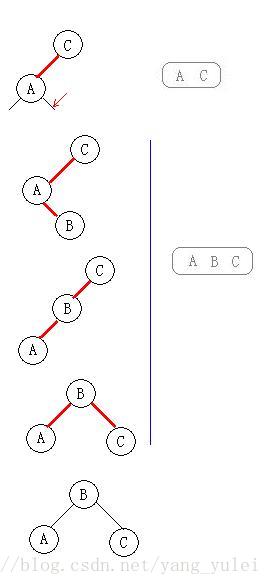
向2-結點中插入新鍵

（向紅黑樹中插入操作時，想想2-3樹的插入操作。紅黑樹與2-3樹在本質上是相同的，只是它們對3結點的表示不同。

向一個只含有一個2-結點的2-3樹中插入新鍵後，2-結點變為3-結點。我們再把這個3-結點轉化為紅結點即可）

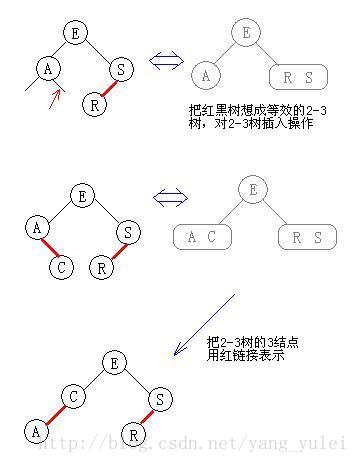
向一顆雙鍵樹（即一個3-結點）中插入新鍵

（向紅黑樹中插入操作時，想想2-3樹的插入操作。你把紅黑樹當做2-3樹來處理插入，一切都變得簡單了）

（向2-3樹中的一個3-結點插入新鍵，這個3結點臨時成為4-結點，然後分裂成3個2結點）

★一顆紅黑樹的構造全過程

平衡二叉樹（AVL樹）

定義：平衡二叉樹(Balance Binary Tree)又稱AVL樹。它或者是一顆空樹，或者是具有下列性質的二叉樹：它的左子樹和右子樹都是平衡二叉樹，且左子樹和右子樹的深度之差的絕對值不超過1。

若將二叉樹上結點的平衡因子BF(BalanceFactor)定義為該結點的左子樹深度減去它的右子樹深度，則平衡因子的絕對值大於1。

其旋轉操作 用2-3樹的分裂來類比想象。

[轉]紅黑樹講解