大部分部落格內容轉載自: https://zhuanlan.zhihu.com/p/24367771

紅黑樹的特性

紅黑樹是一種自平衡的二叉查詢樹，具有二叉查詢樹的特性外，還具有下面特性

1. 每個節點不是紅色就是黑色的；
2. 根節點總是黑色的；
3. 所有的葉節點都是是黑色的（紅黑樹的葉子節點都是空節點（NIL或者NULL））；
4. 如果節點是紅色的，則它的子節點必須是黑色的（反之不一定）；
5. 從根節點到葉節點或空子節點的每條路徑，必須包含相同數目的黑色節點（即相同的黑色高度）。

路徑： 從一個結點到另一個結點，經過的線段條數，也就是結點數量減1
黑深度——從某個結點(不包含結點本身)出發到葉子結點的黑色結點的數量,稱為該節點x的黑深度，記為bd(x)，例如bd(13) = 2,bd(8) =2 
內部結點——紅黑樹的非終結點
外部結點——紅黑樹的葉子節點
 

需要注意的是：

1. 葉子節點是nil的黑色結點

2. 特性5保證了，最大路徑不會操作最小路徑的2倍長度，維持了紅黑樹的平衡。

例如: 圖中，紅黑樹的根節點的黑深度是2，那麼這個紅黑樹的可能的最短路徑(從根節點到葉子節點的路徑上沒有紅色結點)是2，因為紅色節點的子結點不能是紅包結點，只能是黑色結點，而且葉子節點只能是黑色節點，那麼，從根節點到葉子節點的路徑上，最多隻能有2個紅色結點，也就是最長路徑是4，這樣，就保證了紅黑樹的平衡。

紅黑樹的著色和旋轉

著色

紅黑樹的著色，將節點的顏色改變，以滿足2,3,4,5特性

左旋

通常是樹向右傾斜時候，進行左旋操作

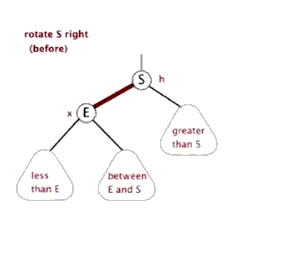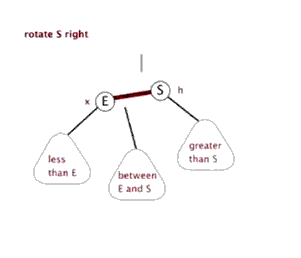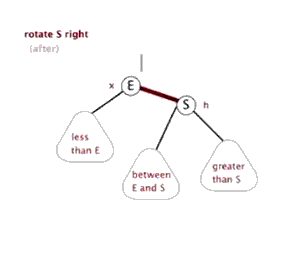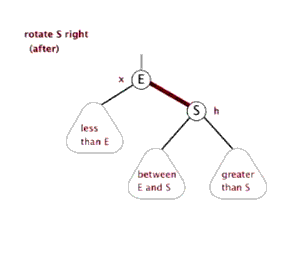
右旋

當樹向左傾斜，進行右旋操作。

紅黑樹的新增

-- 插入結點時候，結點顏色的影響？
如果插入一個黑色節點，根據特性5，從結點到葉子節點的黑色結點數量必須要一致，此時需要調整。
如果插入一個紅色節點，根據特性4，紅色節點的子節點必須是黑色結點。

--- 如此，假設插入的結點是紅色的。

新插入的結點是紅色的，如果遇到父結點是黑色的，修復操作結束，也就是說只有父節點是紅色的時候，需要進行修復。

當父節點是紅色的，下面幾種情況需要修復操作

1. 叔叔結點是紅色

2. 叔叔結點為空，並且祖父結點，父節點，新結點在一條斜線上

3. 叔叔結點為空，並且祖父結點，父節點，新結點不在一條斜線上

插入操作-case 1

case 1的操作是將父節點和叔叔節點與祖父節點的顏色互換，這樣就符合了RBTRee的定義。即維持了高度的平衡，修復後顏色也符合RBTree定義的第三條和第四條。下圖中，操作完成後A節點變成了新的節點。如果A節點的父節點不是黑色的話，則繼續做修復操作。

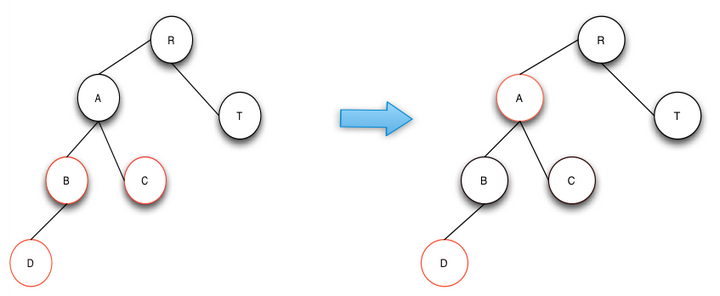
插入操作-case 2

case 2的操作是將B節點進行右旋操作，並且和父節點A互換顏色。通過該修復操作RBTRee的高度和顏色都符合紅黑樹的定義。如果B和C節點都是右節點的話，只要將操作變成左旋就可以了。

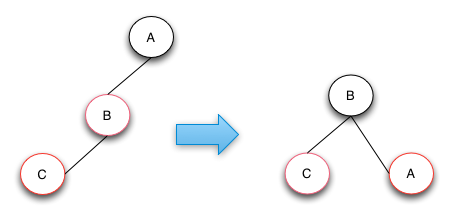
插入操作-case 3

case 3的操作是將C節點進行左旋，這樣就從case 3轉換成case 2了，然後針對case 2進行操作處理就行了。case 2操作做了一個右旋操作和顏色互換來達到目的。如果樹的結構是下圖的映象結構，則只需要將對應的左旋變成右旋，右旋變成左旋即可。

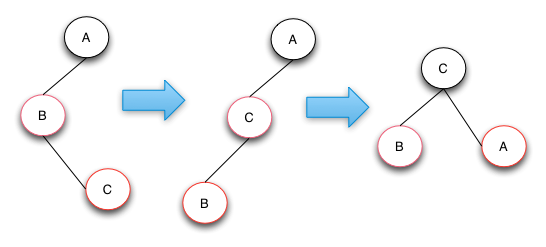
關於插入操作的總結

插入操作的修復過程是向Root結點回溯的過程，一旦涉及的結點符合紅黑樹的定義，修復結束.

刪除操作

紅黑樹的刪除工作首先也是和BST一樣，如果是葉子節點直接刪除，如果不是葉子節點需要找到後繼節點，替換當前結點。

刪除後，紅黑樹可能就不平衡了，需要進行修復操作。

刪除修復操作，針對的是刪除的結點是黑色結點，刪除黑色結點後，紅黑樹變得不平衡，需要從兄弟結點上借掉，如果兄弟結點沒有，只能向上一級回溯，將每一級的黑色結點都減少一個,當回溯到紅色結點或者根節點時候，修復停止。

刪除修復操作分為四種情況(刪除黑節點後)：

1. 待刪除的節點的兄弟節點是紅色的節點。
2. 待刪除的節點的兄弟節點是黑色的節點，且兄弟節點的子節點都是黑色的。
3. 待調整的節點的兄弟節點是黑色的節點，且兄弟節點的左子節點是紅色的，右節點是黑色的(兄弟節點在右邊)，如果兄弟節點在左邊的話，就是兄弟節點的右子節點是紅色的，左節點是黑色的。
4. 待調整的節點的兄弟節點是黑色的節點，且右子節點是是紅色的(兄弟節點在右邊)，如果兄弟節點在左邊，則就是對應的就是左節點是紅色的。

刪除操作-case 1

由於兄弟節點是紅色節點的時候，無法借調黑節點，所以需要將兄弟節點提升到父節點，由於兄弟節點是紅色的，根據RBTree的定義，兄弟節點的子節點是黑色的，就可以從它的子節點借調了。

case 1這樣轉換之後就會變成後面的case 2，case 3，或者case 4進行處理了。上升操作需要對C做一個左旋操作，如果是映象結構的樹只需要做對應的右旋操作即可。

之所以要做case 1操作是因為兄弟節點是紅色的，無法借到一個黑節點來填補刪除的黑節點。

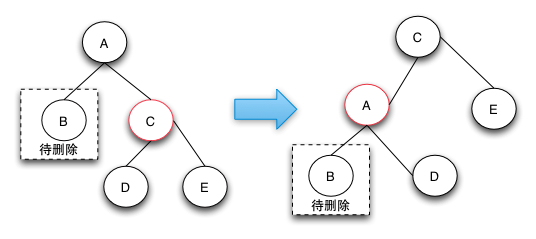
刪除操作-case 2

case 2的刪除操作是由於兄弟節點可以消除一個黑色節點，因為兄弟節點和兄弟節點的子節點都是黑色的，所以可以將兄弟節點變紅，這樣就可以保證樹的區域性的顏色符合定義了。這個時候需要將父節點A變成新的節點，繼續向上調整，直到整顆樹的顏色符合RBTree的定義為止。

case 2這種情況下之所以要將兄弟節點變紅，是因為如果把兄弟節點借調過來，會導致兄弟的結構不符合RBTree的定義，這樣的情況下只能是將兄弟節點也變成紅色來達到顏色的平衡。當將兄弟節點也變紅之後，達到了區域性的平衡了，但是對於祖父節點來說是不符合定義4的。這樣就需要回溯到父節點，接著進行修復操作。

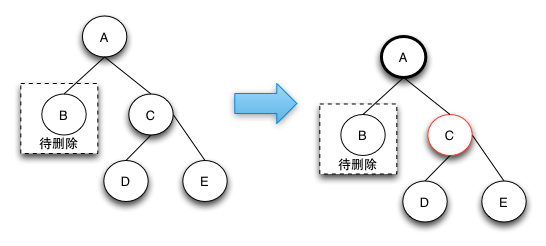
刪除操作-case 3

case 3的刪除操作是一箇中間步驟，它的目的是將左邊的紅色節點借調過來，這樣就可以轉換成case 4狀態了，在case 4狀態下可以將D，E節點都階段過來，通過將兩個節點變成黑色來保證紅黑樹的整體平衡。

之所以說case-3是一箇中間狀態，是因為根據紅黑樹的定義來說，下圖並不是平衡的，他是通過case 2操作完後向上回溯出現的狀態。之所以會出現case 3和後面的case 4的情況，是因為可以通過借用侄子節點的紅色，變成黑色來符合紅黑樹定義4.

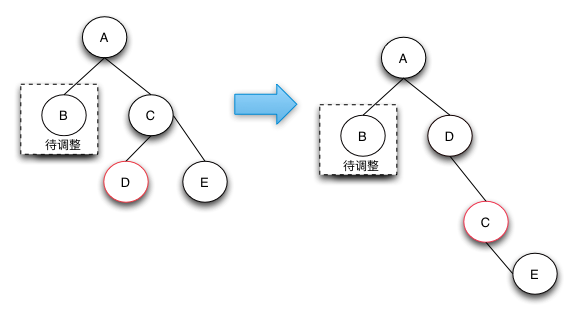
刪除操作-case 4

Case 4的操作是真正的節點借調操作，通過將兄弟節點以及兄弟節點的右節點借調過來，並將兄弟節點的右子節點變成紅色來達到借調兩個黑節點的目的，這樣的話，整棵樹還是符合RBTree的定義的。

Case 4這種情況的發生只有在待刪除的節點的兄弟節點為黑，且子節點不全部為黑，才有可能借調到兩個節點來做黑節點使用，從而保持整棵樹都符合紅黑樹的定義。

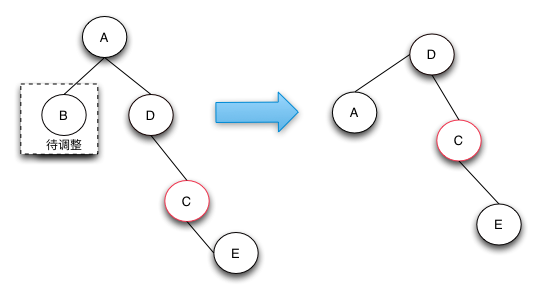
刪除操作的總結

紅黑樹的刪除操作是最複雜的操作，複雜的地方就在於當刪除了黑色節點的時候，如何從兄弟節點去借調節點，以保證樹的顏色符合定義。由於紅色的兄弟節點是沒法借調出黑節點的，這樣只能通過選擇操作讓他上升到父節點，而由於它是紅節點，所以它的子節點就是黑的，可以借調。

對於兄弟節點是黑色節點的可以分成3種情況來處理，當所以的兄弟節點的子節點都是黑色節點時，可以直接將兄弟節點變紅，這樣區域性的紅黑樹顏色是符合定義的。但是整顆樹不一定是符合紅黑樹定義的，需要往上追溯繼續調整。

對於兄弟節點的子節點為左紅右黑或者 (全部為紅，右紅左黑)這兩種情況，可以先將前面的情況通過選擇轉換為後一種情況，在後一種情況下，因為兄弟節點為黑，兄弟節點的右節點為紅，可以借調出兩個節點出來做黑節點，這樣就可以保證刪除了黑節點，整棵樹還是符合紅黑樹的定義的，因為黑色節點的個數沒有改變。

紅黑樹的刪除操作是遇到刪除的節點為紅色，或者追溯調整到了root節點，這時刪除的修復操作完畢。

總結

紅黑樹是平衡二叉樹的一種實現，通過給結點的顏色來保持樹的平衡。紅黑樹在刪除、插入操作之前都是平衡的，刪除、插入操作如果破壞了紅黑樹的平衡，就需要通過著色、旋轉的方式維持平衡。

整個紅黑樹的查詢，插入和刪除都是O(logN)的，原因就是整個紅黑樹的高度是logN，查詢從根到葉，走過的路徑是樹的高度，刪除和插入操作是從葉到根的，所以經過的路徑都是logN。