初探並查集

並查集(Disjoint-Set)是一種優美的數據結構，它擅長動態維護若幹交集為空的集合，並且支持快速合並兩個集合以及查找某個元素所在的集合。
然而這只是並查集所能做的一點微小的工作，文文對並查集的理解是“一種能夠在線維護不同個體之間不可刪除的關系並將其傳遞給之後加入的個體的優美的數據結構”。
光是聽文文這麽說，還是很抽象的，我們不妨來一步一步“發明”並查集吧！

故事背景：

你一天閑得無聊，想要發明一種數據結構。

過程

首先，你想維護不同集合的合並與查詢，於是你決定先找一種方法表示集合。顯然的，你有了兩種思路：

1.維護一個數組 \(f\) ,用 \(f[x]\) 表示元素 \(x\)

但是機靈的你又想到：如果你要合並兩個集合，豈不是要修改很多f數組裏的值嗎？

2.用一棵樹形結構儲存每個集合，樹上的每一個節點都代表一個元素，而每一棵樹的樹根就作為這個集合的代表元素。

每次合並兩個集合的時候，只需要把一棵樹的樹根作為另一棵樹樹根的兒子就好了。你美滋滋的以為自己解決了這個數據結構，直到文文給你拿來了一張極不優美的圖片。

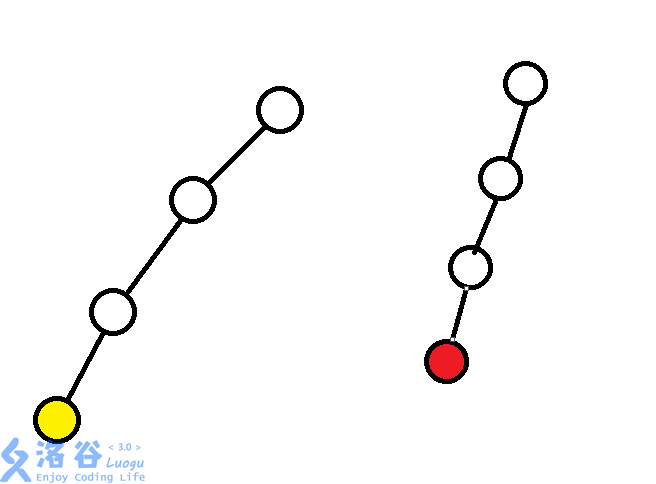
合並黃色節點以及紅色節點所在集合，於是你的數據結構只好一個一個像鏈表一樣，往上跳，跳到樹根，你覺得這種跳法不優美。

你感覺非常悲傷，以為自己的數據結構要泡湯了，但是文文給了你一個思路：不如結婚結合之前的兩種做法，讓他們稍微平衡一下。

你看了看第一種方法，發現他就對應第二種方法裏的這張圖：

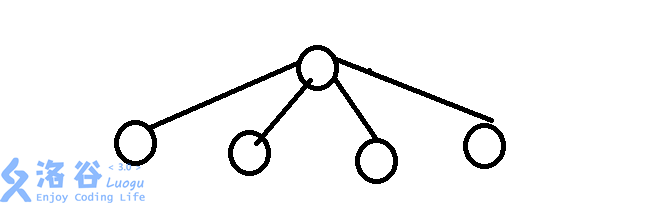
而一個一般的樹形結構，是這樣的：

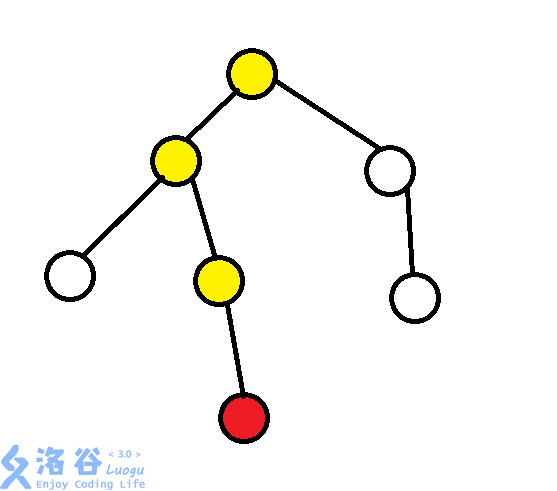
當我們想訪問紅色節點時，我們會沿著黃色節點，一步步跳上來。這個過程不是太優美，並且如果我們多次訪問紅色節點，這條路會走很多次。誒，等等！走很多次？這裏好像有點搞頭啊。

我們不如從這裏優化：每次訪問時，沒有利用到之前訪問時的信息。我們考慮讓每個邊只走一遍，那麽我們就應該把走過的邊廢除掉！我們不妨沿路讓經過的邊統統廢除，經過的點指向根。

上面這張圖，查詢過以後，就變成這樣：

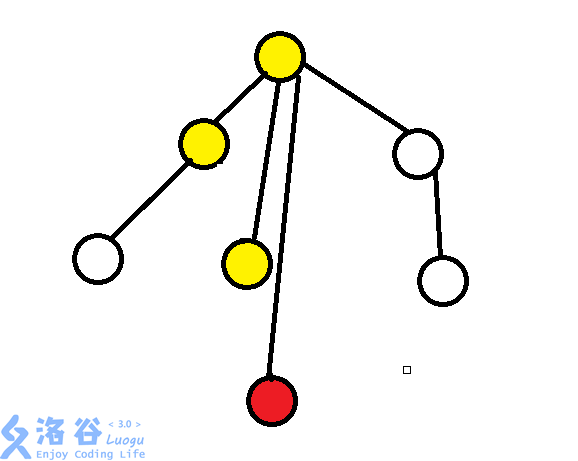
感覺這樣，好像變成了玄學復雜度？實際上是均攤\(O(nlogn)\)的 .

感覺是log級別的吧，你們可以試試閉眼證明法(圖片來自cdcq)

好了，不開玩笑，這個證明起來確實是\(O(logn)\)級別的，但是這個證明相當繁瑣，有興趣的話可以去搜索相關論文。

當然，聰明的你怎麽可能只想到了一種方法呢？你又想到了另一個優化的方法——按秩合並。“秩”一般定義為集合的大小或者集合的深度。

當秩被定義為集合的大小時，按秩合並又被稱為“啟發式合並”。啟發式合並在很多地方上都有體現，應用非常廣泛。

我們每次按秩合並，把秩小的集合合並到秩大的集合，這樣子，對秩大的集合沒有影響，只影響秩小的集合。每次小的集合，向上跳一個，大小至少翻倍，所以最多跳\(log\)次，時間復雜度\(O(logn)\)。

我們考慮把之前所說的兩種優化結合起來，即同時使用按秩合並+路徑壓縮(就是第一種方法的規範名稱)。這個就真的成玄學時間了？但是著名科學家tarjan在1975年發表了一篇論文《Efficiency of a Good But Not Linear Set Union Algorithm》,證明了每次查詢均攤復雜度為\(O(alpha(n))\) 其中，\(alpha\)是反阿克曼函數，證明對應所有的\(n< 2^{2^{10^{19729}}}\)都有\(alpha(n)<5\)

對於一般的題目，路徑壓縮或者按秩合並已經足夠了，沒必要結合起來。

那麽你仔細思考了這個數據結構，他能合並和查詢集合，於是給他起名為“並查集”。

你接下來打算用代碼把剛才的內容實現一下(別哀嚎啦乖，很簡單的)。

首先是初始化，我們還是用\(f\)數組，那麽我們一開始，每個元素單獨成一個集合，我們就這麽做！

for(register int i=1;i<=n;++i) f[i]=i;

你看，很簡單對吧！
然後，考慮查詢操作，我們用\(find\)來實現：

int find(int x) {
    return f[x]==x ? x:fa[x]=find(fa[x]);
}

嗯！上面這個代碼用了一點小trick 他是等價於:

int find(int x) {
    if(f[x]==x) return x;
    f[x]=find(f[x]);
    return f[x];
}

那麽，我們合並的時候怎麽合並呢？

    void merge(int a, int b) {
        int p1 = find(a),p2=find(b);
        if(p1==p2) return;
        f[p1]=p2;
        return;
    }

呼，基本的框架終於搭起來了，你打算馬上試一試這個數據結構，於是去切了點題。

題目推薦：洛谷P3367 P1551

但是，你突然在一道題前面停下了腳步：銀河英雄傳說(洛谷P1196)。

再談並查集

這道題，貌似不能用之前太過於單純的並查集維護了啊！

別急，遇事不決找文文，文文又來給你的並查集升級了哦~

邊帶權與擴展域

並查集是一個樹狀結構，那麽他也是有點和邊的。咱考慮把邊加上權值，表示兩個元素之間的關系哦~

我們維護一個數組\(d\),數值\(d[x]\)表示節點\(x\)與其父節點的關系！

每次路徑壓縮以後，我們都要同時維護\(f[x]\)和\(d[x]\)，這就是所謂的邊帶權。

什麽是擴展域呢？問得好！(謎之音：我沒問啊餵)

擴展域，顧名思義，我們原始並查集只有\(n\)個點，用來表示原本的元素，我們不妨創建\(2n\)個節點，把他們分成兩部分，維護兩種集合。例如我們可以用\(f[x]\)表示元素\(x\)的同類，\(d[x]\)表示元素\(x\)的天敵。我們很快會見到擴展域的應用。

如果有幸的話，文文應該還會發表關於2-SAT的文章，到時候我們就可以研究一下並查集維護的這種關系的本質是什麽了！

有了這兩個強力的武器，你又可以做更多的題目了呢！

推薦題目：洛谷P1196 P2016 P1477 P3207

由於文文水平有限，本文有任何不足之處，歡迎指正，共同交流。

有任何不懂或疑惑之處，可以在luogu官方群(515055655)中搜索文文殿下，一同學習。

[文文殿下]並查集詳細解讀