題目傳送門

社交網絡

題目描述

在社交網絡（social network）的研究中，我們常常使用圖論概念去解釋一些社會現象。不妨看這樣的一個問題。在一個社交圈子裏有n個人，人與人之間有不同程度的關系。我 們將這個關系網絡對應到一個n個結點的無向圖上，兩個不同的人若互相認識，則在他們對應的結點之間連接一條無向邊，並附上一個正數權值c，c越小，表示兩 個人之間的關系越密切。

我們可以用對應結點之間的最短路長度來衡量兩個人s和t之間的關系密切程度，註意到最短路徑上的其他結點為s和t的聯系提供了某種便利， 即這些結點對於s 和t之間的聯系有一定的重要程度。我們可以通過統計經過一個結點v的最短路徑的數目來衡量該結點在社交網絡中的重要程度。

考慮到兩個結點A和B之間可能會有多條最短路徑。我們修改重要程度的定義如下：

令Cs,t表示從s到t的不同的最短路的數目，Cs,t(v)表示經過v從s到t的最短路的數目；則定義

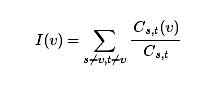
為結點v在社交網絡中的重要程度。

為了使I(v)和Cs,t(v)有意義，我們規定需要處理的社交網絡都是連通的無向圖，即任意兩個結點之間都有一條有限長度的最短路徑。

現在給出這樣一幅描述社交網絡s的加權無向圖，請你求出每一個結點的重要程度。

輸入輸出格式

輸入格式：

輸入第一行有兩個整數，n和m，表示社交網絡中結點和無向邊的數目。在無向圖中，我們將所有結點從1到n進行編號。

接下來m行，每行用三個整數a, b, c描述一條連接結點a和b，權值為c的無向邊。註意任意兩個結點之間最多有一條無向邊相連，無向圖中也不會出現自環（即不存在一條無向邊的兩個端點是相同的結點）。

輸出格式：

輸出包括n行，每行一個實數，精確到小數點後3位。第i行的實數表示結點i在社交網絡中的重要程度。

輸入輸出樣例

4 4
1 2 1
2 3 1
3 4 1
4 1 1

1.000
1.000
1.000
1.000

說明

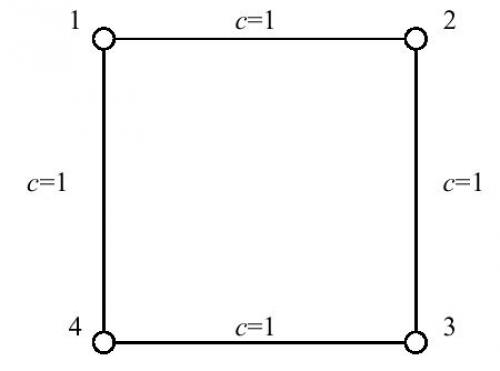
對於1號結點而言，只有2號到4號結點和4號到2號結點的最短路經過1號結點，而2號結點和4號結點之間的最短路又有2條。因而根據定義，1號結點的重要程度計算為1/2+1/2=1。由於圖的對稱性，其他三個結點的重要程度也都是1。

50%的數據中：n ≤10，m ≤45

100%的數據中：n ≤100，m ≤4 500，任意一條邊的權值c是正整數，滿足：1 ≤c ≤1 000。

所有數據中保證給出的無向圖連通，且任意兩個結點之間的最短路徑數目不超過10^10。

　　分析：

　　前幾天做的題，不過現在才寫。

　　首先這個奇奇怪怪的公式先不管，這麽小的數據，當然可以$Floyd$啊。然後把這個公式轉化成中文：以某個點為中心，求經過這個點的兩點之間的最短路條數除以這兩點的最短路的總條數，求個和。那就是最短路計數啊！當然，$Floyd$是可以做最短路計數的，不過蒟蒻當時並不知道。因此我用的是$Dijkstra$，以每個點為起點做一次最短路並求最短路計數即可。然後就是套公式了。

　　Code：

//It is made by HolseLee on 22nd Sep 2018
#include<queue>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N 107
#define M 4507
#define inf 1e9+7
using namespace std;

typedef long long ll;
int n,m,head[N],cnte,f[N][N];
ll s[N][N],p[N],dis[N],d[N][N];
double ans[N];
struct Edge {
    int to,val,nxt;
    Edge() {}
    Edge(const int &_x,const int &_y,const int &_z): to(_x),val(_y),nxt(_z) {}
}e[M<<1];
struct Node {
    int x,d;
    Node() {}
    Node(const int &_x,const int &_y): x(_x),d(_y) {}
    bool operator < (const Node a) const {
        return d>a.d;
    }
};
priority_queue<Node> t;

inline int read()
{
    char ch=getchar(); int num=0; bool flag=false;
    while( ch<‘0‘ || ch>‘9‘ ) {
        if( ch==‘-‘ ) flag=true; ch=getchar();
    }
    while( ch>=‘0‘ && ch<=‘9‘ ) {
        num=num*10+ch-‘0‘; ch=getchar();
    }
    return flag ? -num : num;
}

inline void add(int x,int y,int z)
{
    e[++cnte]=Edge(y,z,head[x]);
    head[x]=cnte;
}

inline void dij(int sta)
{
    for(int i=0; i<=n; ++i)dis[i]=inf, p[i]=0;
    while(!t.empty())t.pop();
    dis[sta]=0, p[sta]=1; t.push(Node(sta,0));
    Node now; int x,y;
    while( !t.empty() ) {
        now=t.top(); t.pop();
        x=now.x; 
        if( dis[x]<now.d ) continue;
        for(int i=head[x]; i; i=e[i].nxt) {
            y=e[i].to;
            if( dis[y]==dis[x]+e[i].val ) {
                p[y]+=p[x];continue;
            } 
            if( dis[y]>dis[x]+e[i].val ){
                dis[y]=dis[x]+e[i].val;
                p[y]=p[x]; t.push(Node(y,dis[y]));
            }
        }
    }
}

int main()
{
    n=read(); m=read();
    int x,y,z;
    for(int i=1; i<=m; ++i) {
        x=read(), y=read(), z=read();
        if( !f[x][y] || f[x][y]>z ) 
            f[x][y]=f[y][x]=z; 
    }
    for(int i=1; i<n; ++i)
    for(int j=i+1; j<=n; ++j) {
        if( !f[i][j] ) continue;
        add(i,j,f[i][j]), add(j,i,f[j][i]);
    }
    for(int i=1; i<=n; ++i) {
        dij(i);
        for(int j=1; j<=n; ++j) {
            s[i][j]=p[j]; d[i][j]=dis[j];
        }
    }
    for(int i=1; i<=n; ++i)
    for(int j=1; j<=n; ++j)
    for(int k=1; k<=n; ++k) 
    if( j!=i && k!=i && j!=k ) {
        if( d[j][i]+d[i][k]!=d[j][k] )continue;
        if( !s[j][k] )continue;
        ans[i]+=(1.0*s[j][i]*s[i][k])/s[j][k];
    }
    for(int i=1; i<=n; ++i)
    printf("%0.3lf\n",ans[i]);
    return 0;
}

洛谷P2047 [NOI2007]社交網絡 [圖論，最短路計數]