2. 程式人生 > >[DP總結]樹形DP

[DP總結]樹形DP

阿新 • • 發佈：2018-10-22
mat 分類 開始 是否 一道 如何 之間 要求 文件

樹形DP

樹形DP，顧名思義，是在樹上進行DP操作，因此往往需要使用DP實現，在轉移時，通常先遞歸求出子樹中的解，再在根節點進行計算轉移。

樹中只有兩種關系，一種是父子關系，一種是平行關系。

下面是幾道簡單的樹形DP。從中我們可以窺出樹形DP的本質。

[luogu] P1352 沒有上司的舞會

題目描述

某大學有N個職員，編號為1~N。他們之間有從屬關系，也就是說他們的關系就像一棵以校長為根的樹，父結點就是子結點的直接上司。現在有個周年慶宴會，宴會每邀請來一個職員都會增加一定的快樂指數Ri，但是呢，如果某個職員的上司來參加舞會了，那麽這個職員就無論如何也不肯來參加舞會了。所以，請你編程計算，邀請哪些職員可以使快樂指數最大，求最大的快樂指數。

輸入輸出格式

輸入格式：

第一行一個整數N。(1<=N<=6000)

接下來N行，第i+1行表示i號職員的快樂指數Ri。(-128<=Ri<=127)

接下來N-1行，每行輸入一對整數L,K。表示K是L的直接上司。

最後一行輸入0 0

輸出格式：

輸出最大的快樂指數。

輸入輸出樣例

輸入樣例#1：

7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5
0 0

輸出樣例#1：

5

最經典的一道題之一。考慮這道題中每個人之間的關系，可以發現每個人的上司可以看做是他的父節點，並且呈樹狀分布，顯然是樹形DP的思路。由於如果某個職員的上司來參加舞會了，那麽這個職員就無論如何也不肯來參加舞會，那麽我們定義\(dp[u][0/1]\)

表示當前選（1）或不選（0）的最大可行值。那麽DP轉移方程顯而易見：\(dp[u][0]+=max(dp[v][0] + dp[v][1])\)和\(dp[u][1]+=dp[v][0]\)其中\(v \in u.to\)

#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <ctime>
#include <iostream>
#include <map>
#include <queue>
#include <vector>
using namespace std;

const int MAXN = 6010;
int n, w[MAXN];
int fa[MAXN], dp[MAXN][2];

struct Edge {
    int nxt, to;
}e[MAXN];

template <typename _Tp>
inline void read(_Tp &x) {
    char ch = getchar( ); bool f = 0; x = 0;
    while (!isdigit(ch)) { if (ch == '-') f = 1; ch = getchar( ); }
    while (isdigit(ch)) { x = x * 10 + ch - '0'; ch = getchar( ); }
    x *= f;
}

int head[MAXN], tot;
inline void AddEdge(int x, int y) {
    e[++ tot].to = y, e[tot].nxt = head[x], head[x] = tot;
}

int Dfs(int u) {
    dp[u][0] = 0, dp[u][1] = w[u];
    for (int i = head[u], v; i; i = e[i].nxt) {
        v = e[i].to;
        Dfs(v);
        dp[u][0] += max(dp[v][0], dp[v][1]);
        dp[u][1] += dp[v][0];
    }
}

int main( ) {
    read(n);
    for (int i = 1; i <= n; ++ i) read(w[i]);
    int L, K; 
    for (int i = 1; i < n; ++ i) {
        read(L), read(K);
        AddEdge(K, L);
        fa[L] = K;
    }
    //尋找根節點
    int rt = 1;
    while (fa[rt]) rt = fa[rt];
    Dfs(rt);
    printf("%d\n", max(dp[rt][0], dp[rt][1]));
    return 0;
}

上面的代碼運行了29ms，不快不慢，標準樹形DP。

還有一種做法，可以達到0ms，時間復雜度直逼\(O(n)\)輸入下界。代碼是這樣的：

#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <ctime>
#include <iostream>
#include <map>
#include <queue>
#include <vector>
using namespace std;

const int MAXN = 6010;
int n, w[MAXN];
int dp[MAXN][2];

template <typename _Tp>
inline void read(_Tp &x) {
    char ch = getchar( ); bool f = 0; x = 0;
    while (!isdigit(ch)) { if (ch == '-') f = 1; ch = getchar( ); }
    while (isdigit(ch)) { x = x * 10 + ch - '0'; ch = getchar( ); }
    x *= f;
}

int main( ) {
    int ans = 0;
    read(n);
    for (int i = 1; i <= n; ++ i) read(dp[i][1]);
    int u, v;
    for (int i = 1; i < n; ++ i) {
        scanf("%d%d", &v, &u);
        dp[u][1] += dp[v][0];
        dp[u][0] += max(dp[v][0], dp[v][1]);
        ans = max(ans, max(dp[u][0], dp[u][1]));
    }
    printf("%d\n", ans);
    return 0;
}

上述代碼直接拋棄了顯性的樹形結構，對於每個輸入的父子節點，在輸入時直接用子節點更新父節點的最優值，利用了線性DP的思想。由此可見，樹形DP是很靈活的，太過拘泥於樹有時反而想不到最優解法。

但是相比較而言，樹形遞歸要比遞推的思路更加顯然，更加清晰，因此在做一些比較復雜，不好遞推的題目時，遞歸Dfs顯然是必須的。

[luogu] P2014 選課

題目描述

在大學裏每個學生，為了達到一定的學分，必須從很多課程裏選擇一些課程來學習，在課程裏有些課程必須在某些課程之前學習，如高等數學總是在其它課程之前學習。現在有N門功課，每門課有個學分，每門課有一門或沒有直接先修課（若課程a是課程b的先修課即只有學完了課程a，才能學習課程b）。一個學生要從這些課程裏選擇M門課程學習，問他能獲得的最大學分是多少？

輸入輸出格式

輸入格式：

第一行有兩個整數N,M用空格隔開。(1<=N<=300,1<=M<=300)

接下來的N行,第I+1行包含兩個整數ki和si, ki表示第I門課的直接先修課，si表示第I門課的學分。若ki=0表示沒有直接先修課（1<=ki<=N, 1<=si<=20）。

輸出格式：

只有一行，選M門課程的最大得分。

輸入輸出樣例

輸入樣例#1：

7  4
2  2
0  1
0  4
2  1
7  1
7  6
2  2

輸出樣例#1：

13

還是顯然的樹形DP。首先要處理的問題是，關於本題的關系結構。細心的同學可能會發現，題目中並沒有保證這是一棵樹，準確來說，本題的關系是一個森林。對於這種結構，我們通常增加一個虛擬節點0，並從0向各個不連通的樹的根連一條邊，使之成為一顆真正的多叉樹。題目中\(k_i=0\)表示沒有直接先修課這個性質實際上簡化了這一問題，這樣只需正常讀入即可保證是一棵根節點為0的樹。

考慮\(dp[i][j]\)表示以\(i\)為根，選了\(j\)個節點的最大值。那麽轉移方程就是\(dp[i][j]=max(dp[v][k] + dp[i][j-k-1]+s[v])\)。表示以\(i\)為根，選了\(j-k-1\)個節點之後，由於要從他的兒子中選節點他自己本身必須選，所以先選上\(v\)節點本身，再從他的一個兒子中選取\(k\)個節點。答案是\(dp[0][m]\)

#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <ctime>
#include <iostream>
#include <map>
#include <queue>
#include <vector>
using namespace std;

const int MAXN = 1010;
int n, m, s[MAXN];
int dp[MAXN][MAXN];

struct Edge {
    int nxt, to;
}e[MAXN];

template <typename _Tp>
inline void read(_Tp &x) {
    char ch = getchar( ); _Tp f = 0; x = 0;
    while (!isdigit(ch)) { if (ch == '-') f = 1; ch = getchar( ); }
    while (isdigit(ch)) { x = x * 10 + ch - '0'; ch = getchar( ); }
    x *= f;
}

int head[MAXN], tot;
inline void AddEdge(int x, int y) {
    e[++ tot].to = y, e[tot].nxt = head[x], head[x] = tot;
}

void Dfs(int u) { 
    for (int i = head[u], v; i; i = e[i].nxt) { 
        v = e[i].to; 
        Dfs(v); 
        for (int j = m; j; -- j) 
            for (int k = j - 1; k >= 0; -- k) 
                dp[u][j] = max(dp[u][j], dp[v][k] + dp[u][j - k - 1] + s[v]);
    }
}

int main( ) {
    read(n), read(m);
    int fa;
    for (int i = 1; i <= n; ++ i) {
        read(fa);
        read(s[i]);
        AddEdge(fa, i);
    }
    Dfs(0);
    printf("%d\n", dp[0][m]);
    return 0;
}

觀察這個轉移方程，我們發現，它與分組背包十分類似。事實上，這道題就是一個經典的樹上分組背包模型。

[luogu] P2015 二叉蘋果樹

題目描述

有一棵蘋果樹，如果樹枝有分叉，一定是分2叉（就是說沒有只有1個兒子的結點）

這棵樹共有N個結點（葉子點或者樹枝分叉點），編號為1-N,樹根編號一定是1。

我們用一根樹枝兩端連接的結點的編號來描述一根樹枝的位置。下面是一顆有4個樹枝的樹

2   5
 \ / 
  3   4
   \ /
    1

現在這顆樹枝條太多了，需要剪枝。但是一些樹枝上長有蘋果。

給定需要保留的樹枝數量，求出最多能留住多少蘋果。

輸入輸出格式

輸入格式：

第1行2個數，N和Q(1<=Q<= N,1<N<=100)。

N表示樹的結點數，Q表示要保留的樹枝數量。接下來N-1行描述樹枝的信息。

每行3個整數，前兩個是它連接的結點的編號。第3個數是這根樹枝上蘋果的數量。

每根樹枝上的蘋果不超過30000個。

輸出格式：

一個數，最多能留住的蘋果的數量。

輸入輸出樣例

輸入樣例#1：

5 2
1 3 1
1 4 10
2 3 20
3 5 20

輸出樣例#1：

21

觀察到本題與上一題十分類似，稍微不同的是，上一題是多叉樹，本題是二叉樹，這對DP本身沒有什麽實質性的影響。註意題目中說道“一些樹枝上長有蘋果”，也就是說蘋果數量並不是點權而是邊權，因此本題的狀態轉移與上一題有細微的差別（將點權變為邊權）。還有一點不同是，題目中的讀入數據並沒有給定明確的父子關系，因此如何建樹是一個問題。這種情況下最常見的方法是將邊建成雙向邊。每次Dfs時，判斷它是否往回指向了父節點，如果是直接跳過，不是則表明當前節點就是子節點。

#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <ctime>
#include <iostream>
#include <map>
#include <queue>
#include <vector>
using namespace std;

const int MAXN = 1010;
int N, Q; 
int dp[MAXN][MAXN];

struct Edge {
    int nxt, to, val;
}e[MAXN << 1];

template <typename _Tp>
inline void read(_Tp &x) {
    char ch = getchar( ); _Tp f = 1; x = 0;
    while (!isdigit(ch)) { if (ch == '-') f = -1; ch = getchar( ); }
    while (isdigit(ch)) x = x * 10 + ch - '0', ch = getchar( );  
    x *= f;
}

int head[MAXN], tot;
void AddEdge(int x, int y, int z) {
    e[++ tot].to = y, e[tot].val = z, e[tot].nxt = head[x], head[x] = tot;
}

void Dfs(int u, int fa) {
    for (int i = head[u], v; ~i; i = e[i].nxt) {
        v = e[i].to;
        if (v == fa) continue;
        Dfs(v, u);
        for (int j = Q; j; -- j)
            for (int k = j - 1; k >= 0; -- k)
                dp[u][j] = max(dp[u][j], dp[v][k] + dp[u][j - k - 1] + e[i].val);
    }
}

int main( ) {
    memset(head, -1, sizeof(head));
    read(N), read(Q);
    int x, y, z;
    for (int i = 1; i < N; ++ i) {
        read(x), read(y), read(z);
        AddEdge(x, y, z);
        AddEdge(y, x, z);
    }
    Dfs(1, 0);
    printf("%d\n", dp[1][Q]);
    return 0;
}

實際上可以加一個小優化，增加一個數組\(cntE[i]\)表示以\(i\)為根的樹的邊數，那麽轉移為

void Dfs(int u, int fa) {
    for (int i = head[u], v; ~i; i = e[i].nxt) {
        v = e[i].to;
        if (v == fa) continue;
        Dfs(v, u);
        cntE[u] += cntE[v] + 1;
        for (int j = min(Q, cntE[u]); j; -- j)
            for (int k = min(j - 1, cntE[v]); k >= 0; -- k)
                dp[u][j] = max(dp[u][j], dp[v][k] + dp[u][j - k - 1] + e[i].val);
    }
}

然而並沒有什麽卵用

[luogu] P1273 有線電視網

題目描述

某收費有線電視網計劃轉播一場重要的足球比賽。他們的轉播網和用戶終端構成一棵樹狀結構，這棵樹的根結點位於足球比賽的現場，樹葉為各個用戶終端，其他中轉站為該樹的內部節點。

從轉播站到轉播站以及從轉播站到所有用戶終端的信號傳輸費用都是已知的，一場轉播的總費用等於傳輸信號的費用總和。

現在每個用戶都準備了一筆費用想觀看這場精彩的足球比賽，有線電視網有權決定給哪些用戶提供信號而不給哪些用戶提供信號。

寫一個程序找出一個方案使得有線電視網在不虧本的情況下使觀看轉播的用戶盡可能多。

輸入輸出格式

輸入格式：

輸入文件的第一行包含兩個用空格隔開的整數N和M，其中2≤N≤3000，1≤M≤N-1，N為整個有線電視網的結點總數，M為用戶終端的數量。

第一個轉播站即樹的根結點編號為1，其他的轉播站編號為2到N-M，用戶終端編號為N-M+1到N。

接下來的N-M行每行表示—個轉播站的數據，第i+1行表示第i個轉播站的數據，其格式如下：

K A1 C1 A2 C2 … Ak Ck

K表示該轉播站下接K個結點(轉播站或用戶)，每個結點對應一對整數A與C，A表示結點編號，C表示從當前轉播站傳輸信號到結點A的費用。最後一行依次表示所有用戶為觀看比賽而準備支付的錢數。

輸出格式：

輸出文件僅一行，包含一個整數，表示上述問題所要求的最大用戶數。

輸入輸出樣例

輸入樣例#1：

5 3
2 2 2 5 3
2 3 2 4 3
3 4 2

輸出樣例#1：

2

說明

樣例解釋

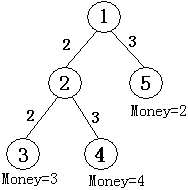
技術分享圖片

如圖所示，共有五個結點。結點①為根結點，即現場直播站，②為一個中轉站，③④⑤為用戶端，共M個，編號從N-M+1到N，他們為觀看比賽分別準備的錢數為3、4、2，從結點①可以傳送信號到結點②，費用為2，也可以傳送信號到結點⑤，費用為3（第二行數據所示），從結點②可以傳輸信號到結點③，費用為2。也可傳輸信號到結點④，費用為3（第三行數據所示），如果要讓所有用戶（③④⑤）都能看上比賽，則信號傳輸的總費用為：

2+3+2+3=10，大於用戶願意支付的總費用3+4+2=9，有線電視網就虧本了，而只讓③④兩個用戶看比賽就不虧本了。

一眼題……依然是個樹上依賴分組背包。\(dp[i][j]\)表示以\(i\)為根節點，選了\(j\)個終端的最大收益。

本題的不同之處在於，選就一定要選到根節點（用戶端），不然顯然虧了。

鑒於本題的特殊性，Dfs寫成int類型比較好。

(我保證下一題一定不是樹上分組背包了)

#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <ctime>
#include <iostream>
#include <map>
#include <queue>
#include <vector>
using namespace std;

const int MAXN = 3010;
int N, M; 
int f[MAXN][MAXN], W[MAXN];

struct Edge {
    int nxt, to, val;
}e[MAXN];

template <typename _Tp>
inline void read(_Tp &x) {
    char ch = getchar( ); _Tp f = 1; x = 0;
    while (!isdigit(ch)) { if (ch == '-') f = -1; ch = getchar( ); }
    while (isdigit(ch)) x = x * 10 + ch - '0', ch = getchar( );  
    x *= f;
}

int head[MAXN], tot;
void AddEdge(int x, int y, int z) {
    e[++ tot].to = y, e[tot].val = z, e[tot].nxt = head[x], head[x] = tot;
}

int Dfs(int u) {
    if (u > N - M) {
        f[u][1] = W[u];
        return 1;
    }
    int sum = 0; //sum表示當前節點子樹中共選了多少終端 
    for (int i = head[u], v; ~i; i = e[i].nxt) {
        v = e[i].to;
        sum += Dfs(v);
        for (int j = sum; j; -- j)
            for (int k = sum; k; -- k) 
                f[u][j] = max(f[u][j], f[v][k] + f[u][j - k] - e[i].val);
    }
    return sum;
}

int main( ) {
    memset(head, -1, sizeof(head));
    read(N), read(M);
    int x, y, k;
    for (int i = 1; i <= N - M; ++ i) {
        read(k);
        for (int j = 1; j <= k; ++ j) {
            read(x), read(y);
            AddEdge(i, x, y);
        }
    }
    for (int i = 1; i <= M; ++ i) read(W[N - M + i]);
    memset(f, -10, sizeof(f));
    for (int i = 1; i <= N; ++ i) f[i][0] = 0; 
    Dfs(1);
    for (int i = M; i; -- i) if (f[1][i] >= 0) {
        printf("%d\n", i);
        break;
    }
    return 0;
}

一定要註意DP數組的初值要足夠小啊QWQ

[luogu] P1270 “訪問”美術館

題目描述

經過數月的精心準備，Peer Brelstet，一個出了名的盜畫者，準備開始他的下一個行動。藝術館的結構，每條走廊要麽分叉為兩條走廊，要麽通向一個展覽室。Peer知道每個展室裏藏畫的數量，並且他精確測量了通過每條走廊的時間。由於經驗老到，他拿下一幅畫需要5秒的時間。你的任務是編一個程序，計算在警察趕來之前，他最多能偷到多少幅畫。

技術分享圖片

輸入輸出格式

輸入格式：

第1行是警察趕到的時間，以s為單位。第2行描述了藝術館的結構，是一串非負整數，成對地出現：每一對的第一個數是走過一條走廊的時間，第2個數是它末端的藏畫數量；如果第2個數是0，那麽說明這條走廊分叉為兩條另外的走廊。數據按照深度優先的次序給出，請看樣例。

一個展室最多有20幅畫。通過每個走廊的時間不超過20s。藝術館最多有100個展室。警察趕到的時間在10min以內。

輸出格式：

輸出偷到的畫的數量

輸入輸出樣例

輸入樣例#1：

60
7 0 8 0 3 1 14 2 10 0 12 4 6 2

輸出樣例#1：

2

這題就比較有意思了。首先輸入就比較有意思……仔細分析發現可以遞歸讀入當前節點的左兒子右兒子，將整張圖抽象成一棵樹。顯然每條走廊來一次，回一次，一共要走兩次，所以時間要乘2。如果當前節點有畫可偷，直接考慮消耗\(i\)的時間可以投多少畫，也就是\(dp[u][i]=min((i - t[u].t) / 5, t[u].p)\)。（別忘了最多只能偷\(t[u].p\)張畫）。沒畫可偷，就意味著有一個分叉道路，也就是需要遞歸左右兒子節點，然後做一次背包即可。所以這是一道經典樹形背包問題。

#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <ctime>
#include <iostream>
#include <map>
#include <queue>
#include <vector>
#define ls (u << 1)
#define rs (u << 1 | 1)
using namespace std;

const int MAXN = 1010;
int S;
int dp[MAXN][MAXN];

struct Tree {
    int t, p;
}t[MAXN];

template <typename _Tp>
inline _Tp read(_Tp &x) {
    char ch = getchar( ); _Tp f = 0; x = 0;
    while (!isdigit(ch)) { if (ch == '-') f = -1; ch = getchar( ); }
    while (isdigit(ch)) { x = x * 10 + ch - '0'; ch = getchar( ); }
    return x * f;
}

void Init(int u) {
    scanf("%d%d", &t[u].t, &t[u].p);
    t[u].t <<= 1;
    if (!t[u].p) Init(ls), Init(rs);
}

void Dfs(int u) {
    if (t[u].p) {
        for (int i = t[u].t; i < S; ++ i) 
            dp[u][i] = min((i - t[u].t) / 5, t[u].p);
        return ;
    }
    Dfs(ls), Dfs(rs);
    for (int i = 1; i < S; ++ i) 
        for (int j = 0; j <= i - t[u].t; ++ j) 
            dp[u][i] = max(dp[u][i], dp[ls][j] + dp[rs][i - t[u].t - j]);
}

int main( ) {
    read(S);
    Init(1);
    Dfs(1);
    printf("%d\n", dp[1][S - 1]);
    return 0;
}

[DP總結]樹形DP

相關推薦

[DP總結]樹形DP

mat 分類 開始 是否 一道 如何 之間 要求 文件 樹形DP 樹形DP，顧名思義，是在樹上進行DP操作，因此往往需要使用DP實現，在轉移時，通常先遞歸求出子樹中的解，再在根節點進行計算轉移。 樹中只有兩種關系，一種是父子關系，一種是平行關系。 下面是幾道簡單的樹形DP。

狀壓DP，樹形DP

樹形DP這個非常特殊，他好像和是唯一一個用深搜實現的DP，所以我們學好它也是應該的，當然，他也是這四個中最簡單的，其特點是通過深搜。 思路： 先找到一個根節點，然後預處理出所有子樹的大小。 然後深搜把最底層的子節點處理出來。 遞歸回溯到根節點，在回溯的時候完成狀態轉移。最後輸出根節點的值。

CF123E Maze（期望dp，樹形dp，式子）

題目連結 題目大意： 給你一棵樹，邊權都是1，每一個點有一個是起點的概率和一個是終點的概率，你將以起點為根，開始在樹上隨機dfs，每到一個點，就會將他的所有兒子隨機打亂成序列，然後按照那個隨機順序走完，直到走到終點。求dfs從起點到終點的期望長度。 其實一開始看到這個題，還是有點懵逼

動態規劃-樹形dp總結

一.簡單的從下到上和從上到下的統計 1.      dp[u]表示以u為根的一共有多少個節點.可以用來求重心. 2.      每個點出發能夠走得最遠的長度.dpm[u], dps[u]用來儲存u為根到子樹的最長距離,注意兩者區別是不同的兒子(不想交路徑).另外有一個f[

hiho1055 - 樹形dp轉換成背包

get urn pro clas 一個 函數計算 val names include 題目鏈接 輸入：一棵樹，每個節點一個權值。 輸出：包括1號節點在內的m個節點組成的連通分量的權值和的最大值 /***************************************

hdu1011 - 樹形dp

max %d bsp algo pid pac add oid can 題目鏈接 #include <set> #include <map> #include <stack> #include <queue> #incl

[vijos 1642]班長的任務 [樹形dp]

c++ 編程 輸出 不能 push_back from || logs 由於 背景 十八居士的畢業典禮（1） 描述 福州時代中學2009屆十班同學畢業了，於是班長PRT開始籌辦畢業晚會，但是由於條件有限，可能每個同學不能都去，但每個人都有一個權值，PRT希望來的同學們

（樹形dp+LCA倍增法）CSU 1915 - John and his farm

const http 題解 def iostream clu algo farm john 題意： 有一個棵樹，現在讓你找兩個點連接起來，這樣必然成為一個環，現在要求這些環長度的期望，也就是平均值。 分析： 第一次做LCA題，做多校的時候，瞎幾把找了模板敲，敲了個八九

POJ題目1947 Rebuilding Roads（樹形dp）

line div space cpp i++ tex tab wan blue Rebuilding Roads Time Limit: 1000MS Memory Limit: 30000K Total Submissions: 9957 Acc

樹形DP 洛谷P2014 選課

ret mem 獲得 學習課程 clu 兩個 tor 輸入輸出格式 scan P2014 選課 題目描述 在大學裏每個學生，為了達到一定的學分，必須從很多課程裏選擇一些課程來學習，在課程裏有些課程必須在某些課程之前學習，如高等數學總是在其它課程之前學習。現在有N門功課，每

HDU-2196 Computer (樹形DP)

color const discuss amp mem [] 應該 str col 最近在看樹形DP，這題應該是樹形DP的經典題了，寫完以後還是有點感覺的。之後看了discuss可以用樹分治來做，以後再試一試。 題目大意 找到帶權樹上離每個點的最遠點。︿(￣︶￣)︿

HDOJ 4705 Y 樹形DP

please order border ssi ont algorithm ack oid ref DP：求出3點構成鏈的方案數 。然後總方案數減去它 Y Time Limit: 2000/1000 MS (Java/Others) Memory Lim

uva 1292 樹形dp

tracking turn oid 狀態 wrap name names code ont UVA 1292 - Strategic game 守衛城市，城市由n個點和n-1條邊組成的樹，要求在點上安排士兵，守衛與點相連的邊。問最少要安排多少士兵。 典型的樹形dp

Codeforces Round #168 (Div. 1) B. Zero Tree 樹形dp

max cin 只需要 進行 push ack sin turn its 題目鏈接： http://codeforces.com/problemset/problem/274/B 題意： 給出一棵樹，每個點有權值，每次操作可以對一個聯通子集中的點全部加1，或者全部減1，且每

多叉樹轉二叉樹+樹形dp（codevs 1746 貪吃的九頭龍 2002noi）

main bsp 搜索 我們 bre define div 思考 import 題目傳送門 看到這個題目我們要先把問題簡化了，條件中是多叉樹，我們可以把它轉換成二叉樹，左邊是兒子右邊是兄弟的儲存方式。 首先先判斷否的部分，當總的果子小於需求，也就是N-k<M-1時

Codeforces 627D Preorder Test(二分+樹形DP)

bug eof scan pla k個結點 comment 最大 tdi tac 題意：給出一棵無根樹，每個節點有一個權值，現在要讓dfs序的前k個結點的最小值最大，求出這個值。 考慮二分答案，把>=答案的點標記為1，<答案的點標記為0，現在的任務時使得df

【bzoj1907】樹的路徑覆蓋 樹形dp

scan log print data 狀態 代碼 str 單獨 .com 題目描述 輸入 輸出 樣例輸入 1 7 1 2 2 3 2 4 4 6 5 6 6 7 樣例輸出 3 題解 樹形dp 設f[x]表示以x為根的子樹完成

【BZOJ2466】[中山市選2009]樹 樹形DP

消元 滿足 cpp ret 之前 中山市選 所有 不理解 高斯消元 【BZOJ2466】[中山市選2009]樹 Description 圖論中的樹為一個無環的無向圖。給定一棵樹，每個節點有一盞指示燈和一個按鈕。如果節點的按扭被按了，那麽該節點的燈會從熄滅變為點亮（

BZOJ1040 基環森林 找環+基礎樹形DP

pri script 矛盾 add 順序 自己 任務 樹形dp 按順序 1040: [ZJOI2008]騎士 Time Limit: 10 Sec Memory Limit: 162 MBSubmit: 4752 Solved: 1831[Submit][Status

洛谷P2018 消息傳遞 樹形DP

sin con log sum iostream lib bsp dfs cst 洛谷P2018 消息傳遞 樹形DP dp[ u ] 表示 u 節點 已經被傳到，然後將其字節點都傳到所需要的最少時間 可知一個原則 一個樹中的子樹中如果同時開始傳，那麽最晚才能傳到