這道題采用權值線段樹合並的解法。

首先講一下解法中出現的兩個概念：權值線段樹與線段樹合並。

所謂權值線段樹，可以理解為維護的信息反過來的普通線段樹，我個人認為值域線段樹這個名字其實要準確一些。

舉個例子，我們將序列$1,1,2,3,4,4,4,5,6,6$中的數依次插入，那麽插入完成之後的效果圖大概是下面這樣的：

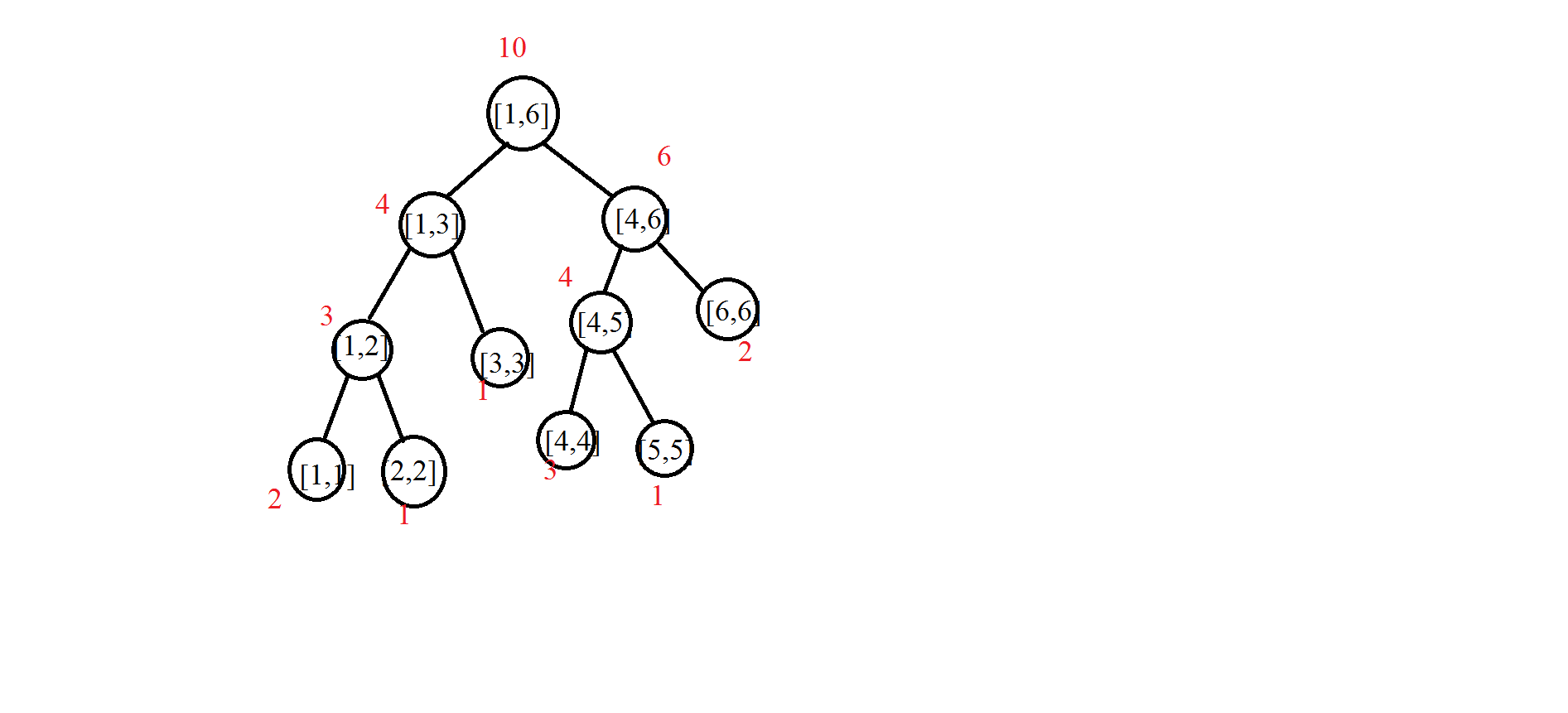
（其中紅色為節點的值）

也就是說，每一個節點維護的值是這個區間內的數出現的次數。

在實現權值線段樹時，我們通常會采用動態開點的方式，也就是不創建無關的節點，當然也可以離散化數據，否則必然會空間超限。

而線段樹合並的原理則是基於線段樹較為穩定的結構。

在合並的過程中，我們將兩顆線段樹對應位置的節點的值合在一起，創建一顆新的線段樹。

過程大致如下：

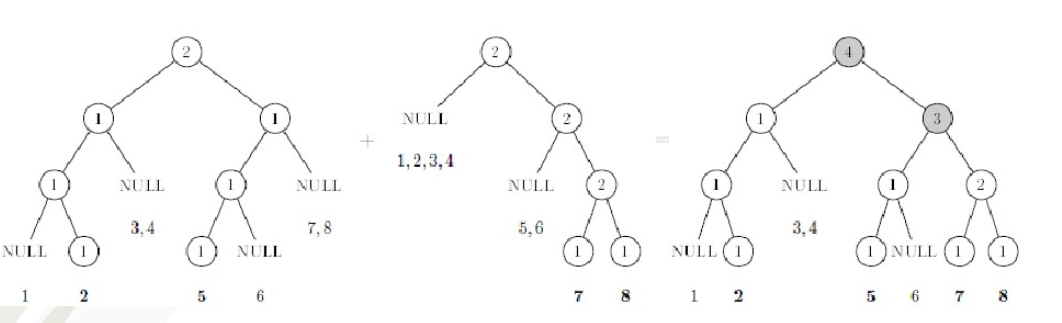
這道題讓我們求出逆序對個數最小值，並且允許我們隨意交換一個節點的兩棵子樹。

考慮一個任意的節點，它的子樹先序遍歷後的逆序對顯然只有三種組成：

1. 左子樹中

2. 右子樹中

3. 跨越左右子樹

對子樹的交換顯然不會影響第1,2類，因此我們只需要計算出第三類的最小值即可。

至於計算則沒有什麽難度。由於我們維護的是值域，因此左兒子必定比右兒子大，那麽我們就用左兒子大小乘以右兒子大小即可得出交換前逆序對個數。交換後同理之。

這裏需要註意，我們能夠這樣計算是因為無論左右兒子怎麽交換，影響的都只有當前部分的逆序對個數，而不會影響深度更淺的節點的值。

另：這道題處理輸入十分窒息，可參考樓下寫法。

AC代碼如下：

509ms 57236kb

 1 #include<bits/stdc++.h>
 2 
 3 using namespace std;
 4 
 5 namespace StandardIO {
 6 
 7     template<typename T>inline void read (T &x) {
 8         x=0;T f=1;char c=getchar();
 9         for (; c<‘0‘||c>‘9‘; c=getchar()) if (c==‘-‘) f=-1
 
;
10         for (; c>=‘0‘&&c<=‘9‘; c=getchar()) x=x*10+c-‘0‘;
11         x*=f;
12     }
13 
14     template<typename T>inline void write (T x) {
15         if (x<0) putchar(‘-‘),x*=-1;
16         if (x>=10) write(x/10);
17         putchar(x%10+‘0‘);
18     }
19 
20 }
21 
22 using namespace StandardIO;
23 
24 namespace Solve {
25     
26     const int N=200200;
27     
28     int n;
29     long long ans,ans1,ans2;
30     int tot_node;
31     struct node {
32         int ls,rs;
33         long long val;
34     } tree[N*20];
35     
36     void update (int l,int r,int v,int &pos) {
37         if (!pos) pos=++tot_node;
38         tree[pos].val++;
39         if (l==r) return;
40         int mid=(l+r)>>1;
41         if (v<=mid) update(l,mid,v,tree[pos].ls);
42         else update(mid+1,r,v,tree[pos].rs);
43     }
44     void merge (int &x,int y) {
45         if (!x||!y) {
46             x=x+y;return;
47         }
48         tree[x].val+=tree[y].val;
49         ans1+=(long long)tree[tree[x].rs].val*tree[tree[y].ls].val;
50         ans2+=(long long)tree[tree[x].ls].val*tree[tree[y].rs].val;
51         merge(tree[x].ls,tree[y].ls);
52         merge(tree[x].rs,tree[y].rs);
53     }
54     void dfs (int &x) {
55         int tmp,ls,rs;x=0;
56         read(tmp);
57         if (!tmp) {
58             dfs(ls),dfs(rs);
59             ans1=ans2=0;
60             x=ls,merge(x,rs);
61             ans+=min(ans1,ans2);
62         } else update(1,n,tmp,x);
63     }
64 
65     inline void solve () {
66         read(n);
67         int tmp=0;
68         dfs(tmp);
69         write(ans);
70     }
71 }
72 
73 using namespace Solve;
74 
75 int main () {
76 //    freopen(".in","r",stdin);
77 //    freopen(".out","w",stdout);
78     solve();
79 }

題解 P3521 【[POI2011]ROT-Tree Rotations】