地統計分析筆記——探索資料
在執行地統計分析之前,瀏覽、熟悉、檢查自己的資料是至關重要的。繪製和檢查資料是地統計分析過程中的必要階段,我們可以從這些工作中獲得一些先驗知識,指導後續的工作。
Stage 1 繪製資料
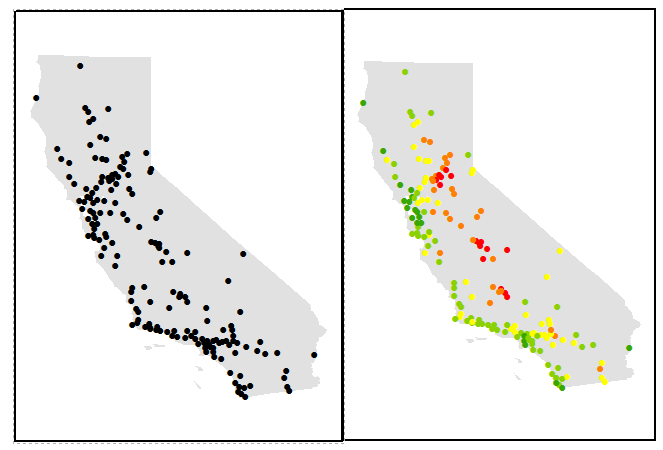
通過ArcMap的圖層渲染方案繪製資料,我們可以獲得對資料的第一印象。
例如,使用單一符號渲染瞭解取樣點的疏密分佈,通過分類渲染瞭解取樣點高值低值的分佈,等等。
Stage 2 檢查資料
繪製資料後,使用 探索性空間資料分析 (Exploratory Spatial Data Analysis,ESDA) 工具來執行資料探索的第二階段。這些工具提供了一種比繪製資料更加量化的方式來檢查資料,有助於我們更深入地瞭解正在研究的現象,有助於我們對插值模型的構建方式做出更加正確的決策。
ESDA 工具包括:
Ⅰ 是否服從正態分佈?
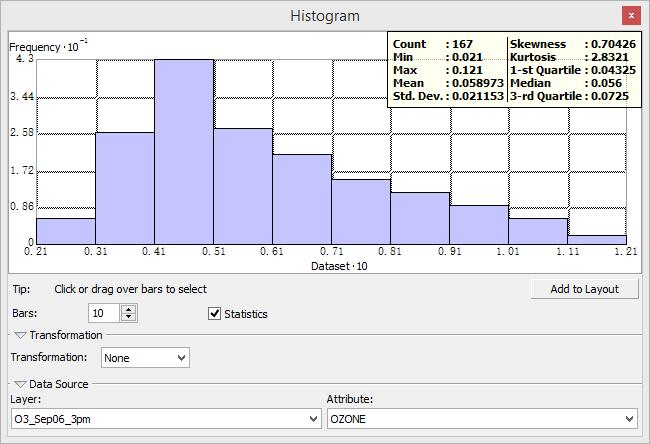
Histogram/直方圖
直方圖用於顯示感興趣資料集的頻率分佈並計算彙總統計資料,如何解讀圖形和統計資訊呢?
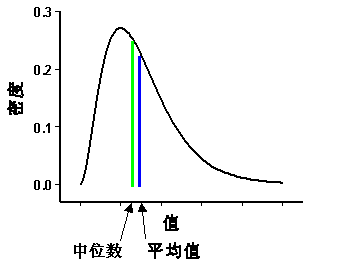
- 如果資料服從正態分佈,則平均值(mean)與中值(median)類似,偏度(skewness)應接近零,並且峰度(kurtosis)應接近 3。
- 平均值即為資料的算數平均值。平均值提供分佈中心的測量值。 中位數與累積比例 0.5 對應。如果資料以升序排列,50%的值位於中間值之下,50% 的值位於中間值之上。中間值提供了分佈中心的另一個測量值。 第一和第三分位數分別與累積比例 0.25 和 0.75 對應。如果資料以升序排列,則 25% 的值位於第一分位數之下,25% 的值位於第三分位數之上。第一和第三分位數是分位數的特殊情況。
- 偏度係數是分佈對稱度的測量值。對於對稱的分佈,偏度係數為零。如果分佈具有較長的大值右尾部,則為正偏分佈;如果分佈具有較長的小值左尾部,則為負偏分佈。對於正偏分佈,平均值大於中間值;對負偏分佈,平均值小於中間值。
- 峰度取決於分佈尾部的大小,提供分佈產生異常值可能性的衡量指標。正態分佈的峰度等於三。具有較厚尾部的分佈被稱為高峰態,其峰度大於三。具有較薄尾部的分佈被稱為低峰態,其峰度值小於三。
- 資料的方差,通常對過高值或過低值很敏感。標準差為方差的平方根,它描述了資料在平均值周圍的分散程度。方差和標準差越小,測量值聚類相對於平均值就越緊密。
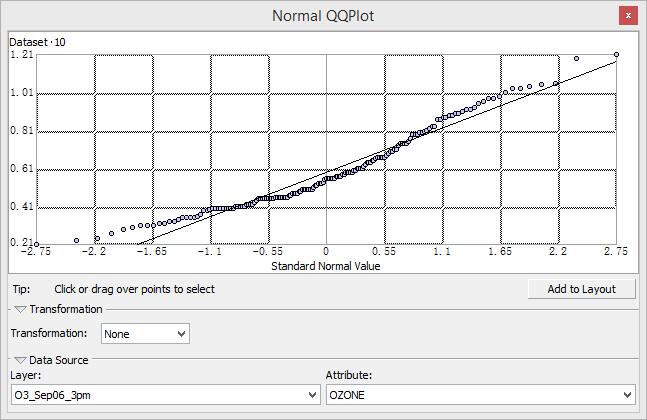
Normal QQPlots/正態QQ圖
正態 QQ 圖上的點可指示資料集的單變數分佈的正態性。如果資料是正態分佈的,點將落在 45 度參考線上。如果資料不是正態分佈的,點將會偏離參考線。
General QQPlots/普通QQ圖
普通 QQ 圖用於評估兩個資料集的分佈的相似程度。這些圖的建立和所述的正態 QQ 圖的過程類似,不同之處在於第二個資料集不一定要服從正態分佈,使用任何資料集均可。如果兩個資料集具有相同的分佈,普通 QQ 圖中的點將落在 45 度直線上。
### 有關資料變換
Geostatistical Analyst 中的一些插值方法要求資料呈正態分佈。如果資料偏斜(分佈不均衡),則可能需要將資料變換為正態分佈。
Box-Cox 變換(又稱冪變換)
如果在某一部分研究區域中計數值很小,這一區域的變異性就小於計數值更大的另一區域的變異性。在這種情況下,平方根變換將有助於使整個研究區域內的方差更加恆定,通常還會使資料呈正態分佈。平方根變換是 Box-Cox 變換中 λ = ½ 時的特例。對數變換
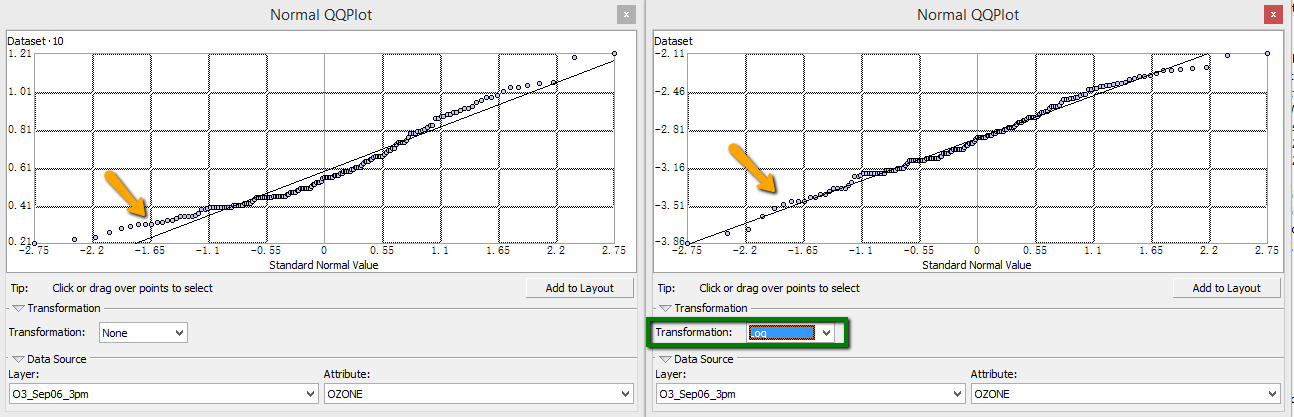
對數變換實際上是 Box-Cox 變換中 λ = 0 時的特例。對數變換通常用於呈正偏分佈的資料。其中有些值非常大,如果這些大值位於研究區域中,對數變換有助於使方差更加恆定和歸一化資料。例如資料如下分佈:
變換前後對比:
反正弦變換
反正弦變換可用於表示比例或百分比的資料。通常在資料為比例形式時,方差在接近 0 和 1 時最小,接近 0.5 時最大。反正弦變換有助於使整個研究區域內的方差更加恆定,通常還會使資料呈正態分佈。
Ⅱ 是否存在異常值?
全域性異常值是相對於資料集中的所有值而言具有非常高值或非常低值的已測量取樣點。
區域性異常值是一個已測量取樣點,其值處於整個資料集的正常值域範圍內,但檢視周圍點時,其值則顯得異常高或異常低。
如果異常值是現象中的真實異常情況,那麼這可能是研究和理解現象的最重要的位置點。如果異常值是由資料輸入過程中的錯誤所導致的,那麼在建立表面之前應該對其進行校正或移除。
Histogram/直方圖
如果在直方圖的最左側(極小值)或最右側(極大值)能夠看到一個孤立的條,可能表明這個條所表示的點是異常值。這種條越孤立於直方圖的主條組,點是異常值的概率就越大。
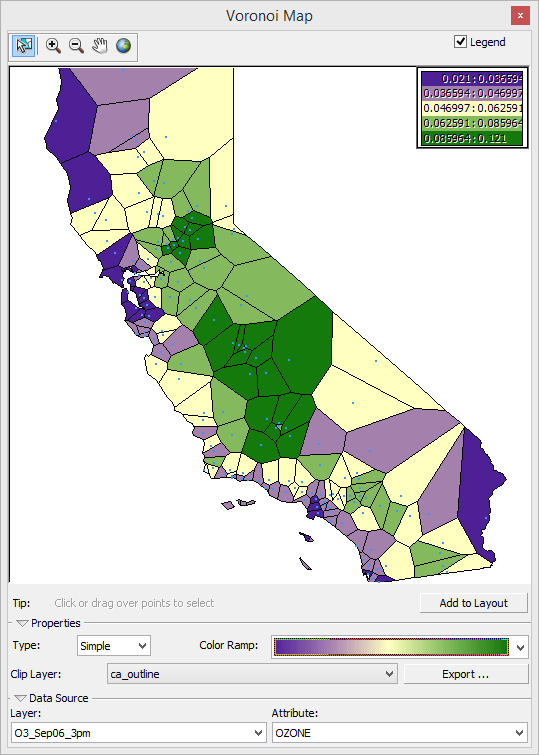
Voronoi 圖
Voronoi 圖是由取樣點形成的泰森多邊形地圖。
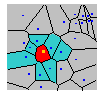
在檢視 Voronoi 圖時,檢查附近是否有面符號色彩差別很大的值。
例如,下圖中紅色面明顯異於周圍值。
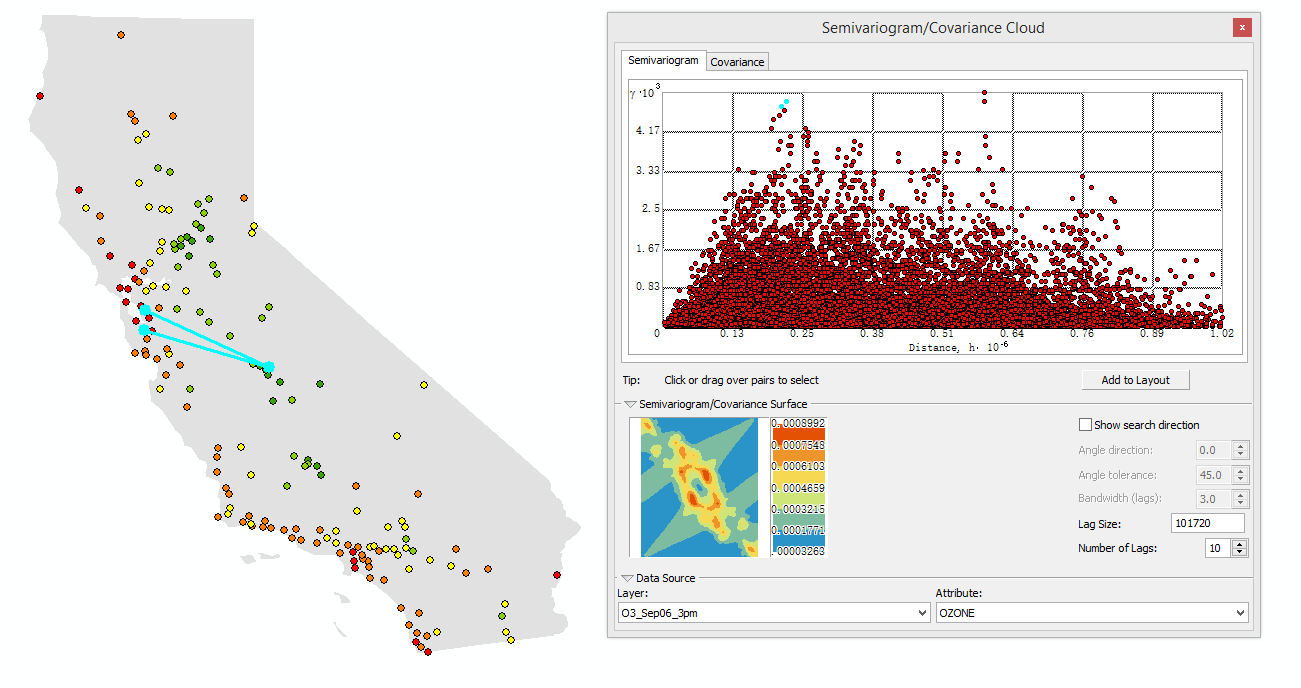
Semivariogram/Covariance Cloud / 半變異函式/協方差雲
半變異函式/協方差雲工具可以用來檢查資料集中空間自相關的區域性特徵以及查詢區域性異常值。
雲中的每個點表示資料集中的一對點,x 軸表示各位置間的距離,y 軸表示這些位置上的值的差值平方。半變異函式中的每個點都表示一個位置對,而不是地圖上的單個位置。因此雲中點的數量會隨著資料集中點的數量的增加而快速增加。如果資料集中存在 n 個點,則半變異函式/協方差雲中將顯示 n*(n-1)/2 個點。因此,不建議使用點數超過幾千個的資料集。如果資料集包含幾千個點,那麼應使用子集要素工具來隨機選擇點,然後在半變異函式/協方差雲中使用子集。
“半變異函式/協方差雲”工具對檢測區域性異常值特別有用。它們顯示為互相接近的點(x 軸上的低值),但在 y 軸上卻是高值,表明組成點對的兩個點的值有很大差異。這與所期望的結果正相反,即互相接近的點有相似的值。
Ⅲ 是否存在趨勢?
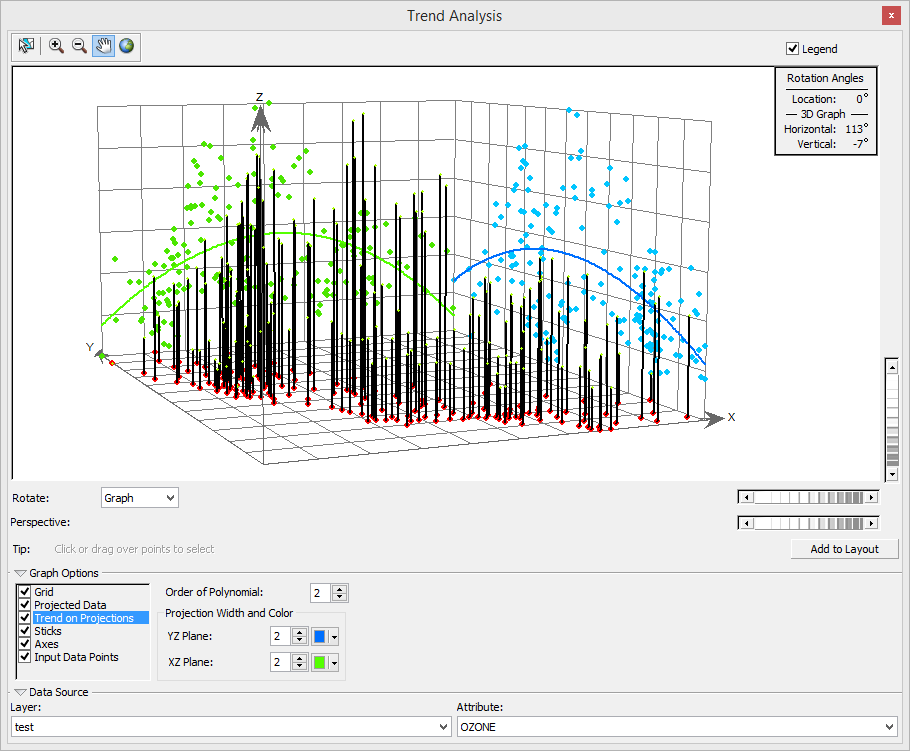
Trend Analyst / 趨勢分析
“趨勢分析”工具提供資料的三維透檢視。取樣點的位置繪製在 x,y 平面上,z值表示感興趣的屬性值。趨勢分析工具將散點圖投影到 x,z 平面和 y,z 平面上,通過多項式曲線對每個投影進行了擬合。
瀏覽圖形垂直牆面上的粗線。這些線表示趨勢。一條趨勢線沿 x 軸(通常表示縱向趨勢),另一條顯示沿 y 軸的趨勢(通常表示緯度趨勢)。如果經過投影點的曲線是平的,則不存在趨勢;如果多項式曲線具有確切的模式(如下圖的藍線和綠線),這表明資料中存在某種趨勢。
另外,檢查趨勢時更改多項式的階非常有用;檢查不同於標準 N–S 和 E–W 方向的趨勢非常有幫助,可以通過旋轉趨勢軸檢查資料。
Ⅳ 是否空間自相關?
我們可通過檢查不同的位置的取樣資料對來探索資料的空間自相關,仍然使用前面提到過的ESDA工具半變異函式雲。
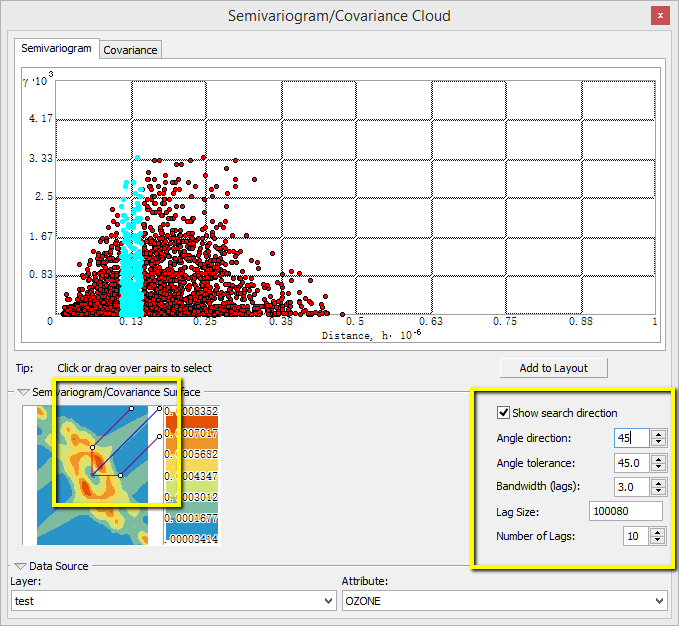
Semivariogram/Covariance Cloud / 半變異函式/協方差雲
如果存在空間相關性,則距離較近的點對(在 x 軸的最左側)應具有較小的差值(在 y 軸上的值較小)。隨著各個點之間的距離越來越大(點在 x 軸上向右移動),通常,差值的平方也應隨之增大(在 y 軸上向上移動)。通常,平方差超過某個距離後就會保持不變。超過這個距離的位置對被視為不相關。
如果半變異函式中的點對構成一條水平的直線,那麼資料中可能不存在空間自相關,因而對資料進行插值也就失去了意義。
地統計方法的基本假設是,對於任意兩個彼此間的距離和方向都相近的位置,其差值的平方也應相近。這種關係稱為平穩性。空間自相關可能僅依賴於兩個位置之間的距離,這被稱為各向同性。如果事物在某些方向上比在其他方向上更相似,也就是半變異函式和協方差中都存在這種方向性影響,它被稱為各向異性。
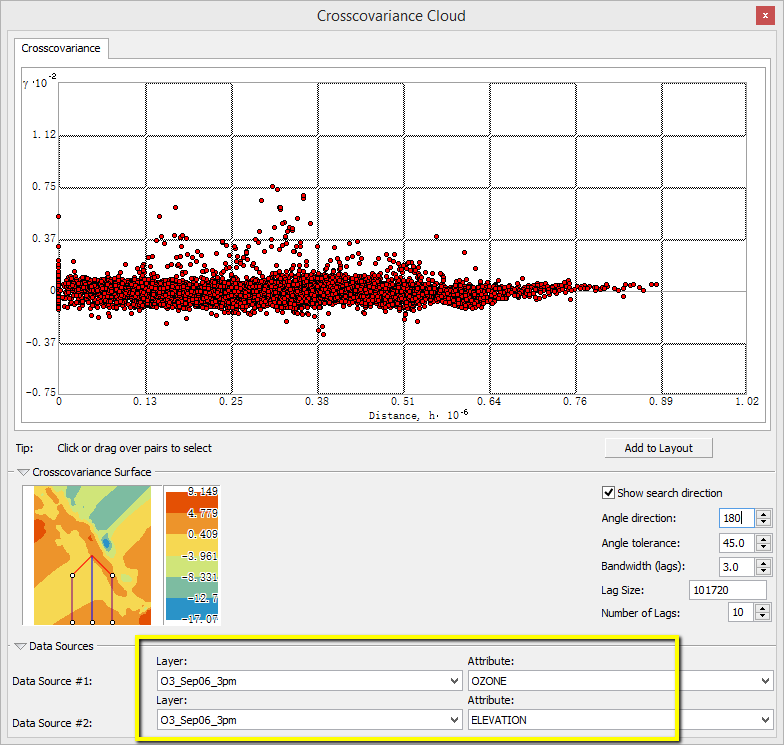
交叉協方差雲
“交叉協方差雲”工具可用於研究兩個資料集之間的交叉相關。交叉協方差雲顯示了兩個資料集間的所有位置對的經驗交叉協方差,並且將其作為兩位置間距離的函式對其進行繪製,與上面的工具類似,該工具也提供具有搜尋方向功能的協方差表面。
對資料有了第一印象,並且用 ESDA 工具對資料做了檢查,我們已經對待研究的資料有了一些先驗知識,那麼下面就可以選擇插值方法來建立表面了,下一篇繼續。