活動選擇問題_貪心演算法
貪心演算法
對於許多最優化問題,使用動態規劃演算法來求最優解有些殺雞用牛刀了,可以使用更加簡單、更加高效的演算法。貪心演算法就是這樣的演算法,它在每一步做出當時看起來最佳的選擇。也就是說它總是做出區域性最優的選擇,從而得到全域性最優解。
對於某些問題並不保證得到最優解,但對很多問題確實可以求得最優解。
思想
貪心演算法的基本思路是從問題的某一個初始解出發一步一步地進行,根據某個優化測度,每一步都要確保能獲得區域性最優解。每一步只考慮一個數據,他的選取應該滿足區域性優化的條件。若下一個資料和部分最優解連在一起不再是可行解時,就不把該資料新增到部分解中,直到把所有資料列舉完,或者不能再新增演算法停止 [3]
過程
-
建立數學模型來描述問題;
-
把求解的問題分成若干個子問題;
-
對每一子問題求解,得到子問題的區域性最優解;
-
把子問題的解區域性最優解合成原來解問題的一個解。
活動選擇問題
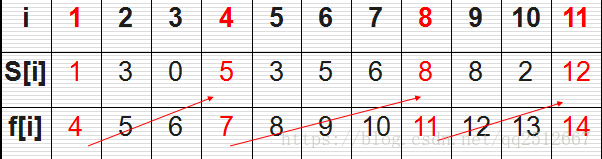
有n個需要在同一天使用同一個教室的活動a1,a2,…,an,教室同一時刻只能由一個活動使用。每個活動ai都有一個開始時間si和結束時間fi 。一旦被選擇後,活動ai就佔據半開時間區間[si,fi)。如果[si,fi]和[sj,fj]互不重疊,ai和aj兩個活動就可以被安排在這一天。該問題就是要安排這些活動使得儘量多的活動能不衝突的舉行(最大相容活動子集)。例如下圖所示的活動集合S,其中各項活動按照結束時間單調遞增排序。
{a3,a9,a11}是一個相容的活動子集,但它不是最大子集,因為子集{a1,a4,a8,a11}更大,實際上它是我們這個問題的最大相容子集,但它不是唯一的一個{a2,a4,a9,a11}
貪心演算法
想要使用貪心演算法的話,得先找到適合貪心演算法的規律(區域性最優選擇)
對於任何非空的活動集合S,假如am是S中結束時間最早的活動,則am一定在S的某個最大相容活動子集中。
(如何證明上面的結論?反證法)
遞迴解決
迭代解決
static void Main(string[] args) { int[] s = { 0, 1, 3, 0, 5, 3, 5, 6, 8, 8, 2, 12}; int[] f = { 0, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 }; List<int> list = ActivitySelection(1, 11, 0, 24, s, f); foreach (int item in list) { Console.Write(item + " "); } } static List<int> ActivitySelection(int startNum, int endNum, int startTime, int endTime, int[] s,int [] f) { if (startNum>endNum||startTime>=endTime) { return new List<int>(); } int tempNum=0; //從第一個開始找 for (int number = startNum; number <=endNum; number++) { if (s[number]>=startTime&&f[number]<=endTime ) //在開始和 結束的 活動時間 區間內 { //找到了 tempNum = number; break; } } // 找 剩餘的 List<int> Activitylist= ActivitySelection(tempNum + 1, endNum, f[tempNum], endTime,s, f); Activitylist.Add(tempNum); return Activitylist; }
迭代解決
static void Main(string[] args)
{
int[] s = { 0, 1, 3, 0, 5, 3, 5, 6, 8, 8, 2, 12, 24 };
int[] f = { 0, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 24 };
int startTime = 0;
int endTime = 24;
List<int> list = new List<int>();
for (int number = 1; number <=11; number++)
{
//說明 活動
if (s[number]<=startTime&&f[number]<=endTime)
{
list.Add(number);
startTime = f[number];//下次判斷的時候就是從下次的
//結束時間判斷
}
}
foreach (int i in list)
{
Console.WriteLine(i);
}
}