Andrew機器學習課程 章節2——單變數線性迴歸
在surpervised question中
(x,y)表示一個訓練樣本。 x為features(特徵)y為target(目標)
(xi,yi)表示訓練集。上標i just an index into the training set
Hypothesis function(假設函式):
Hypothesis function : hθ(x) =θ0+θ1x.
Hypothesis function是關於變數x的函式
cost fuction(代價函式)
概況來講,任何能夠衡量模型預測出來的值h(θ)與真實值y之間的差異的函式都可以叫做代價函式C(θ),如果有多個樣本,則可以將所有代價函式的取值求均值,記做J(θ)。
cost fuction是關於parameters的函式
平方誤差代價函式是解決迴歸問題最常用的手段,具體定義如下:
找到是訓練集中預測值和真實值的差的平方和最小的1/2M的θ0和θ1的值
假設有訓練樣本(x, y),模型為h,引數為θ0,θ1。hθ(xi) =θ0+θ1xi.
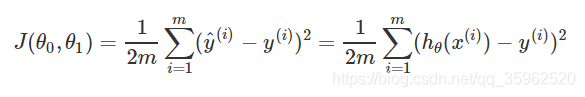
優化目標: 求使得J(θ0,θ1)最小的parameters:θ0,θ1。此時求得目標函式
梯度下降法:(grandient descent)
給θ0,θ1賦予某一個初值進行出發 直到收斂於某一個區域性最小解
演算法過程:重複下列迭代

其中:=表示的是複製,α表示學習率(控制以多大的幅度更新引數)通俗講,用於表示下降的步伐。
特別注意:θ0,θ1需要同時更新
α太小:需要進行多次梯度下降
α太大:可能越過最小點,導致無法收斂甚至發散
一個特點:在梯度下降法中,當我們接近區域性最低點時,梯度下降法自動採取更小的幅度(曲線越來越平緩導致導數也越來越小)
線性迴歸演算法:
(將梯度演算法與代價函式相結合擬合線性函式)
求導:

線性迴歸的代價函式總是像一個弓狀函式如下所示。叫做凸函式(convex function)
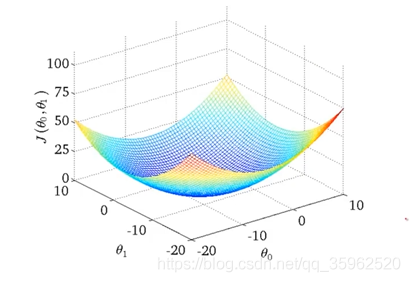
此類函式沒有區域性最優解,只有一個全域性最優。
”batch“gradient descent
