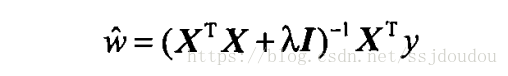機器學習-嶺迴歸python實踐【2】
阿新 • • 發佈:2018-11-01
寫在最前面:
當資料的特徵大於樣本點,線性迴歸就不能用了,因為在計算[(X^T)*X]的逆時候,n>m,n是特徵,m是樣本點,此時的輸入矩陣不是滿秩矩陣,行列式為0。
此時,我們可以使用嶺迴歸(ridge regression)
閱讀本文前,需要各位簡單回憶一下線性代數知識,關於矩陣的秩
簡單來說,嶺迴歸就是在矩陣(X^T)*X的基礎上加上λI,這樣使得矩陣非奇異,從而能對(XTX)-1+λI整體求逆(矩陣X的轉置乘矩陣X再求逆矩陣,實在是不會打數學公式,相信大家都能看的懂哈),其中,I是一個m✖️m的單位矩陣,這樣我們的迴歸係數變成了
下面上程式碼
。
。
。
截圖
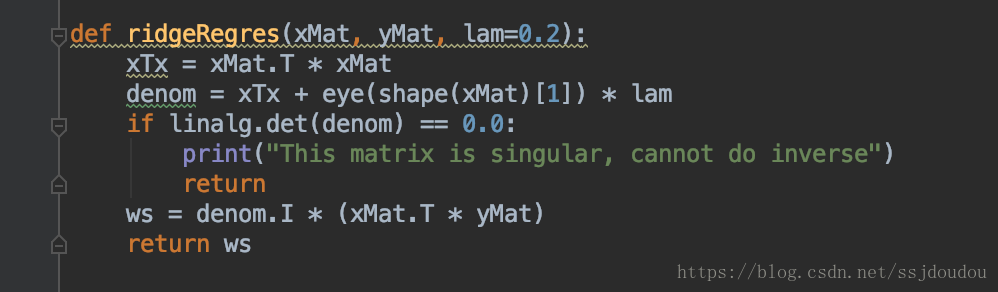
這個函式首先構建矩陣X^T ✖️ X,然後用lam乘以單位矩陣,預設lam為0.2,此時不排除lam為0的情況,所以還是需要對行列式進行一下非0判斷。
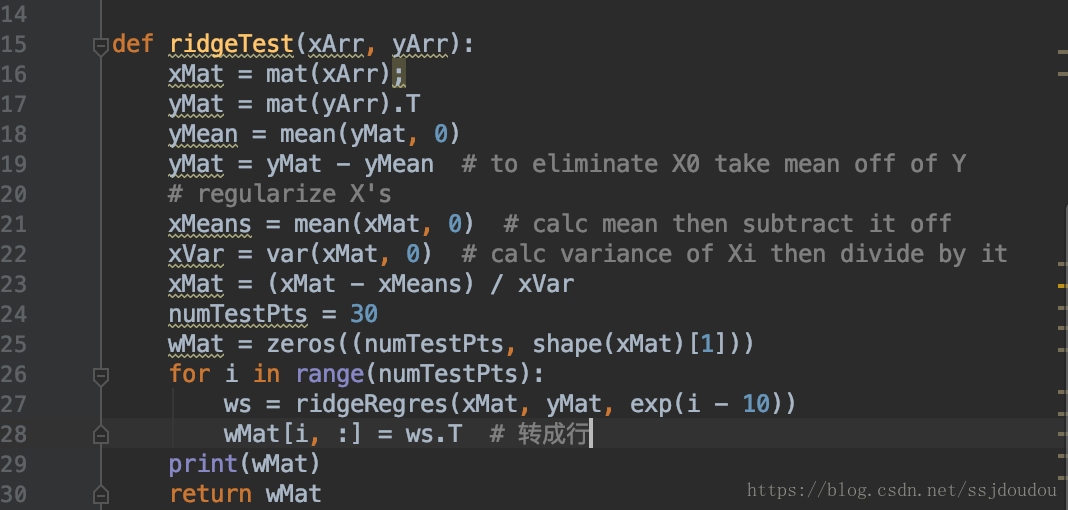
上面是資料標準化
具體做法是所有特徵減去各自的均值併除以方差
也可以計算標準差,std函式,標準差是方差開根號
載入資料
這樣就得到了30個不同lambda對應的迴歸係數
簡單介紹幾個numpy常用的函式
mat:建立矩陣
mean:求均值
var:求方差
exp:指數
這裡的lambda採用指數級變化,可以較快、和更明顯的看出lambda在取值很小和很大的情況下,對結果造成的影響,將所有迴歸係數輸出到一個矩陣並返回:
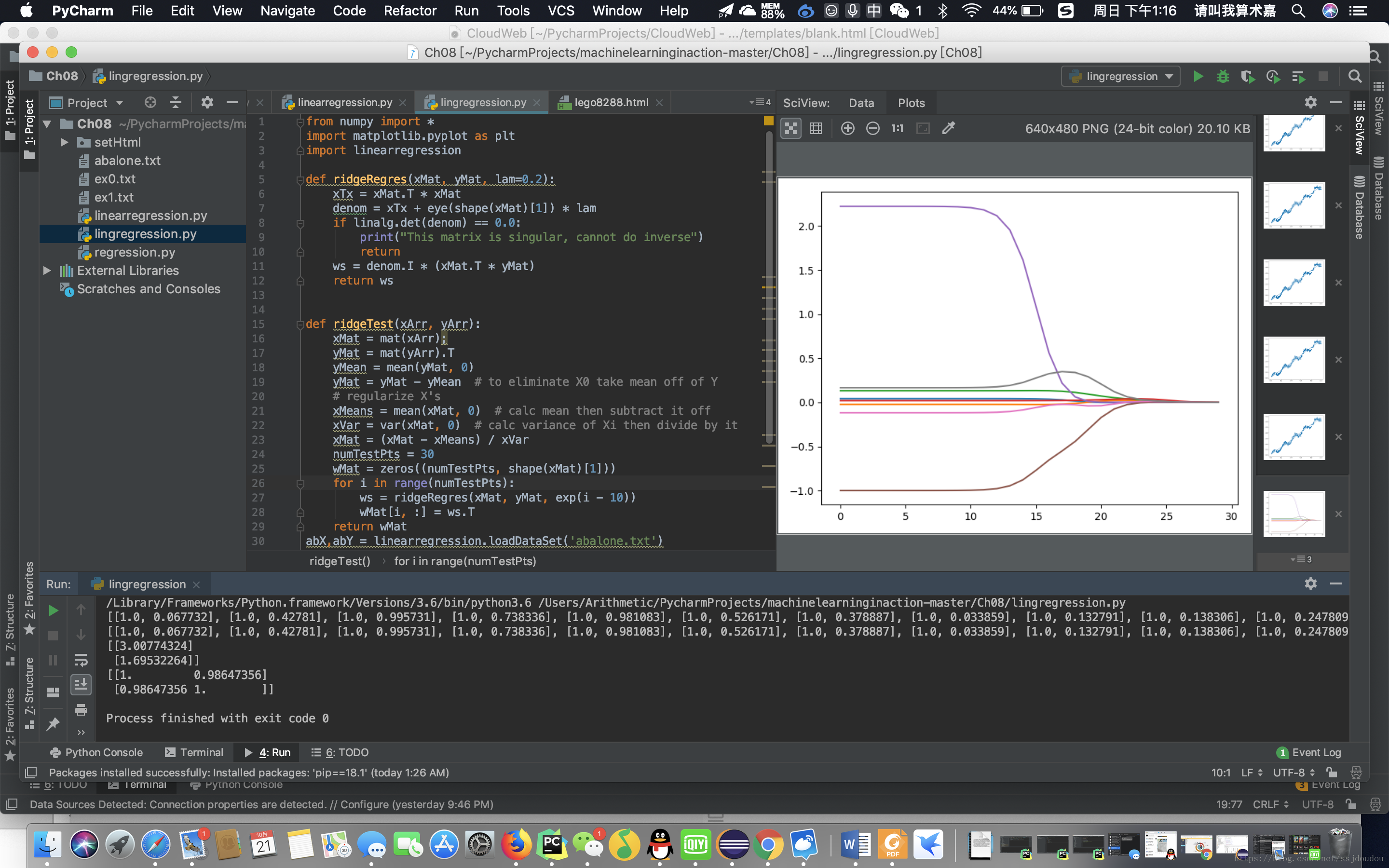
橫座標為log(λ),縱座標為迴歸係數
當λ無限趨於0時,此時就是線性迴歸
當λ變大時,迴歸係數為0,此時也沒有任何意義
在中間部分的某值可以取到比較好的預測效果
今天就到這裡,好睏啊,大家有啥想看的可以私我微信:18351922995