Classification

• 一.資料集獲取及預處理

  • 1 資料集匯入

  • 2資料集劃分

• 二、binary classification 二元分類器

  • 自己實現交叉驗證函式
  • confusion matrix
  • precision/recall tradeoff
  • Precision/Recall曲線
  • ROC 曲線
  • AUC

• 三、Multiclass Classification

  • Error Analysis
  • numpy broadcast

• 四、 Multilabel Classification 多標籤分類

• 五、Multioutput Classification

最常見的監督學習問題是分類和迴歸問題，此章我們利用mnist資料集完成分類問題的探討

一.資料集獲取及預處理

1. 資料集匯入

注意： 資料集匯入需要連外網，我將資料集儲存在這裡

# 引入資料集
from sklearn.datasets import fetch_mldata
import os
import pickle
# 若檔案中沒存在mnist資料集，則將資料集從網站匯入後存入到檔案中，
# 若存在直接從檔案中獲取
 

if not os.path.exists('mnist.pickle'):
    mnist = fetch_mldata('MNIST original')
    with open('mnist.pickle', 'wb') as wf:
        pickle.dump(mnist, wf)
else:
    with open('mnist.pickle', 'rb') as rf:
        mnist = pickle.load(rf)
        
mnist

out:

{‘DESCR’: ‘mldata.org dataset: mnist-original’,
‘COL_NAMES’: [‘label’, ‘data’],
‘target’: array([0., 0., 0., …, 9., 9., 9.]),
‘data’: array([[0, 0, 0, …, 0, 0, 0],
[0, 0, 0, …, 0, 0, 0],
[0, 0, 0, …, 0, 0, 0],
…,
[0, 0, 0, …, 0, 0, 0],
[0, 0, 0, …, 0, 0, 0],
[0, 0, 0, …, 0, 0, 0]], dtype=uint8)}

X,y = mnist['data'], mnist['target']
print(X.shape)
print(y.shape)

out:

(70000, 784)
(70000,)

顯示一張圖片 每張圖片為 28×2828×28 的灰度圖，利用matplotlib imshow()函式隨機畫一張圖

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

import matplotlib
number = np.random.choice(len(X))
some_digits = X[number]
some_digits_image = some_digits.reshape(28, 28)

plt.imshow(some_digits_image, cmap=matplotlib.cm.binary, interpolation='nearest')
plt.axis('off')

y[number]

out:

6.0

2.資料集劃分

將資料集分為測試集和訓練集， 並將訓練集中的資料順序打亂(shuffle the training set).這將保證所有的交叉驗證子集相似，不至於某些子集缺少了某些數字。
注意：某些學習演算法對訓練資料個體的順序十分敏感，如果連續輸入很多相似的資料，演算法的表現效能很糟糕；但是對於某些時間序列資料而言比如股票票價和天氣狀況等，打亂順序並非好事

X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
# print(np.unique(y_train))
shuffle_index = np.random.permutation(60000)
X_train, y_train = X_train[shuffle_index], y_train[shuffle_index]

二、binary classification 二元分類器

1.建立分類器

簡單點，先訓練一個二元分類器(Binary classifier)，比如判斷一個數字是否為5.
np.unique解釋 https://docs.scipy.org/doc/numpy/reference/generated/numpy.unique.html

# 重新更改標籤
y_train_5 = (y_train == 5.0 )
y_test_5 = (y_test == 5.0 )
# 檢查標籤的種類
np.unique(y_train_5)
# print(y_test)
# y_test_5

out:

array([False, True])

選擇基於隨機梯度下降（ SGD， stochastic gradient descent）的分類器,該梯度下降演算法一次只使用一個樣本訓練演算法，更容易處理大量訓練資料，所以SGD也適合於線上學習（online learning）.建立一個SGDClassifier

from sklearn.linear_model import SGDClassifier

sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(X_train, y_train_5)

out: 訓練的SGDClassifier

SGDClassifier(alpha=0.0001, average=False, class_weight=None, epsilon=0.1,
eta0=0.0, fit_intercept=True, l1_ratio=0.15,
learning_rate=‘optimal’, loss=‘hinge’, max_iter=None, n_iter=None,
n_jobs=1, penalty=‘l2’, power_t=0.5, random_state=42, shuffle=True,
tol=None, verbose=0, warm_start=False)

預測影象 上文中some_digits

sgd_clf.predict([some_digits])

out:

array([False])

2. 模型評價

評估一個分類器通常要比評估迴歸模型更困難，更具有技巧性，所以本章大多數討論的主題都是評估問題

使用交叉驗證測量準確率

關於交叉驗證詳解 https://blog.csdn.net/dss_dssssd/article/details/82860175
自己實現交叉驗證函式：

• StratifiedKFold完成分層抽樣，即將資料分成k個folds.然後StratifiedKFold.split返回k個元組的生成器，每個元組的第一個值為訓練索引，第二個值為驗證索引值
• clone(estimator) : Constructs a new estimator with the same parameters. 使用與estimator相同的引數新建立一個新的estimator

from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone
# 分為3個folds
skfolds = StratifiedKFold(n_splits=3, random_state=42)
# print(list(skfolds.split(X_train, y_train_5)))
for train_index, test_index in skfolds.split(X_train, y_train_5):
    # print(train_index.shape,test_index)
    
    #先建立一個新的estimator
    clone_clf = clone(sgd_clf)
    
    X_train_folds = X_train[train_index]
    y_train_folds = (y_train_5[train_index])
    X_test_fold = X_train[test_index]
    y_test_fold = (y_train_5[test_index])
    clone_clf.fit(X_train_folds, y_train_folds)
    y_pred = clone_clf.predict(X_test_fold)
    n_correct = sum(y_pred == y_test_fold)
    print(n_correct / len(y_pred))
    

out:

0.92935
0.96545
0.9593

使用sklearn提供的cross_val_score函式

from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring='accuracy')

out:

array([0.92935, 0.96545, 0.9593 ])

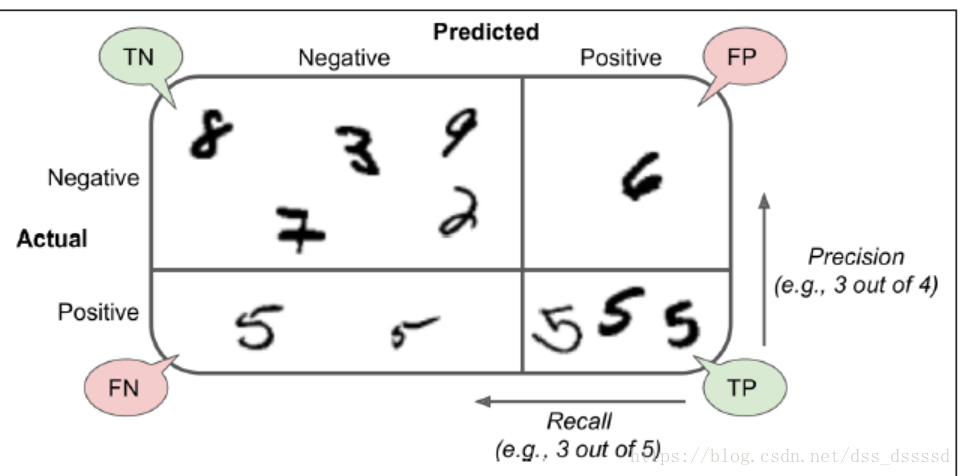
confusion matrix

將類A分類為B的次數，比如你想檢視將5識別為3的次數，你可以檢視矩陣的第5行第3列。
在計算混淆矩陣(confusion matrix)之前，先需要預測值，以便於與真實值比較，當然可以在測試集（test set）上預測，但是現在先不在測試集上預測（切記，只有在專案的最後再能使用測試集），可以使用cross_val_predict()在訓練集上預測代替。
和cross_val_score()函式相似，cross_val_predict()也在k個子集上做交叉驗證，但返回的不是評估分數，而是在每個測試集上的預測值。簡單的就是，每次在k-1個子集上訓練，而在餘下的1個子集上預測。

以下就是利用cross_val_predict()和confusion_matrix()函式獲得混淆矩陣的例子

from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
from sklearn.metrics import confusion_matrix
confusion_matrix(y_train_5, y_train_pred)

out:

array([[52660, 1919],
[ 999, 4422]], dtype=int64)

在混淆矩陣中，每一行為真實的類別（actual class），每一列為預測的類別（predict class），比如第一行的類別為不是5（被稱為 the negative class）的圖片，有52660被正確的分類(true negativse)，而有1919的圖片被分為5(false positives)，第二行的類別為5（the positive class），有999的圖片分類為不是5（false negatives），有4422的圖片分類為 true positives）。注意： positive或negative依據的是預測的類別

幾個描述分類結果的度量標準(metric):

• precision:

預測為真的分類中，真正為真的類別所佔的比列

$precision = \frac{TP}{TP +FP}$

• recall (sensitivity true positive rate(TPR)):

真正為真的分類中，預測為真的類別所佔的比列

$recall = \frac{TP}{TP+FN}$

計算precision和recall

from sklearn.metrics import precision_score, recall_score
precision_score(y_train_5, y_train_pred)

out:

0.6973663460022078

4422 / (1919 +4422)

out:

0.6973663460022078

recall_score(y_train_5, y_train_pred)

out:

0.8157166574432761

4422 / (4422 +999)

out:

0.8157166574432761

預測為5的類別只有大約為70%預測正確，而真正為5的類別只有約81%預測出來。

F1

F1的定義，將precision和recall結合起來，如果precision和recall很高，（這是我們對一個優秀的演算法所期待的），那麼F1將很高

$F1 = \frac{2}{\frac{1}{precision} + \frac{1}{recall}}$

from sklearn.metrics import f1_score
f1_score(y_train_5, y_train_pred)

out:

0.7519129399761946

在一些場合下我們關注precision,而在另一些場合下，我們更關注recall，比如，如果你想訓練一個分類器來檢測出對孩子而言安全的視訊，你更想可以拒絕很多安全的視訊（low recall），但是保留的視訊最好是全是安全的（high precision），而在另一個場合下，你訓練另一個通過商店監控視訊分類小偷的分類器，你希望寧可只有30%的precision卻必須要有99%的recall

但是卻不能同時使兩者都很高，增加precision必然伴隨著降低recall，反之亦然，被稱為precision/recall tradeoff

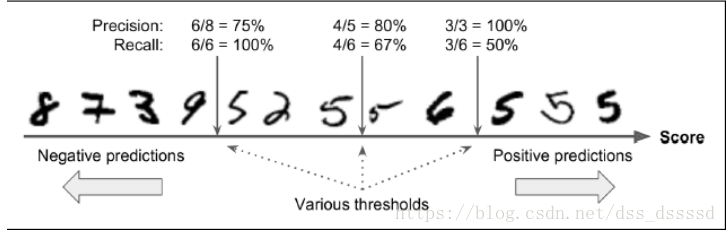
讓我們通過上圖來了解一下，precision/recall tradeoff：
對於每一個圖片，SGDClassifier首先會根據decision function計算一個
分數（score），如果該分數大於某一個閾值（threshold），則分為positive 類，否則分為negative類，首先假設threshold是上圖中間的箭頭，則此時precision為5個識別為5的手寫字型中有4個為5，即4/5=0.8,而真正為5的6個手寫字型中識別出來4個，即4/6=0.67,而此時若提高閾值到右邊的箭頭則，precision=3/3=1,reall=3/6=0.5,同樣降低閾值，則提高了recall而降低了precision

設定threshold來分類

sklearn不允許你直接設定閾值（threshold），卻允許你通過使用決策分數（decision score）來做預測。

不再呼叫分類器的predict()函式，呼叫decision_function()函式，該函式返回的是每一幅圖片（每一個例項個體）的分數，接下來基於得到的分數，使用你想設定的閾值來判斷

y_scores = sgd_clf.decision_function([some_digits])
y_scores

out:

array([-413834.30335973])

threshold = -600000
y_some_dogit_perd = (y_scores > threshold)
y_some_dogit_perd

out:

array([ True])

SGDClassfier使用的閾值threshold為0，所以返回結果為假
那麼，如何確定使用什麼閾值呢？仍然使用cross_val_predict()函式，指定method引數為decision_function,獲得驗證集上所有例項的得分。

y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3,method="decision_function")

PR曲線

使用得到的分數，對於所有可能的閾值，可以使用precision_recall_curve函式來計算precision和recall

precision_recall_curve 官方文件

使用matplotlib畫圖片時， 注意precisions和recalls的長度與threshold不一致，大1

from sklearn.metrics import precision_recall_curve
precisions, recalls , threshold = precision_recall_curve(y_train_5, y_scores)

def plot_precision_recall_vs_threshold(precisions, recalls, threshold):
    
    plt.plot(threshold, precisions[:-1 ], "b--", label="Precisions")
    plt.plot(threshold, recalls[:-1], "g--", label="Recall")
    plt.xlabel("Threshold")
    plt.legend(loc="upper left")
    plt.ylim([0, 1])

plot_precision_recall_vs_threshold(precisions, recalls, threshold)
plt.show()

注意: 上圖中，Precisions的曲線要比Recalls更加不平滑，那是因為當提高閾值時，precision可能會降低，而recall則一定會降低，看一下之前講述precision和recall的例子，可得，當提高閾值時， 原來識別為5的圖片未識別出來導致，precision從4/5=0.8講到了3/4=0.75.

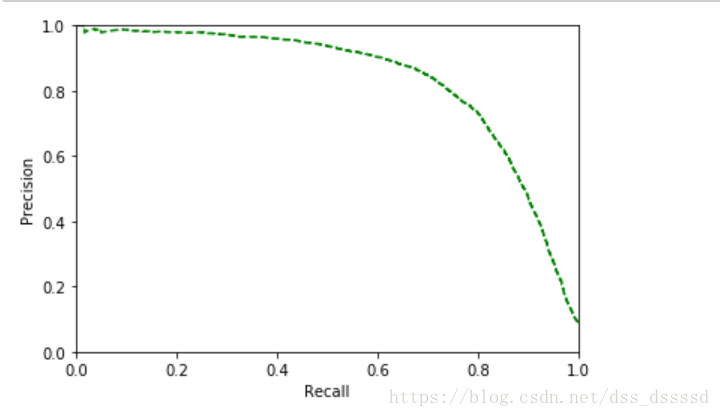
也可以直接畫出precision和recall的變化曲線

def plot_precision_vs_recall(precisions, recalls):
    
    plt.plot(recalls, precisions, "g--")
    plt.ylabel("Precision")
    plt.xlabel("Recall")
    plt.ylim([0, 1])
    plt.xlim([0, 1])
    

plot_precision_vs_recall(precisions, recalls)

從圖中可以看出，recall從60%出開始快速下降，假設選擇90%的precision，看第一個圖，發現大概threshold大約為65000，此時再預測新的資料時， 不再呼叫predict()函式，而是先呼叫decision_function(),獲得y_scores，然後使用設定的閾值預測。

y_train_pred_90 = (y_scores > 70000)
# 判斷此時的precision和recall
#不幸的是，precision達不到要求
precision_score(y_train_5, y_train_pred_90)

out:

0.8066599394550958

recall_score(y_train_5, y_train_pred_90)

out:

0.7373178380372625

ROC 曲線

ROC曲線（receiever operating characteristic）與precision/recall曲線相似，但刻畫的是true positive rate[TPR]（recall的另一個名字）和false positive rate[FPR]之間的關係。FPR是錯誤的被分為正樣本的負樣本的個數與負樣本個數的比值，等於 $1 - TNR$；

TNR(true negative rate)：負樣本中被正確分為負樣本的個數與負樣本個數的比值，TNR也被稱為specificity，因此ROC曲線刻畫的是sensitivity（recall）和 1 - specificity之間的關係。

先計算TPR和FPR，使用roc_curve()函式

from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)

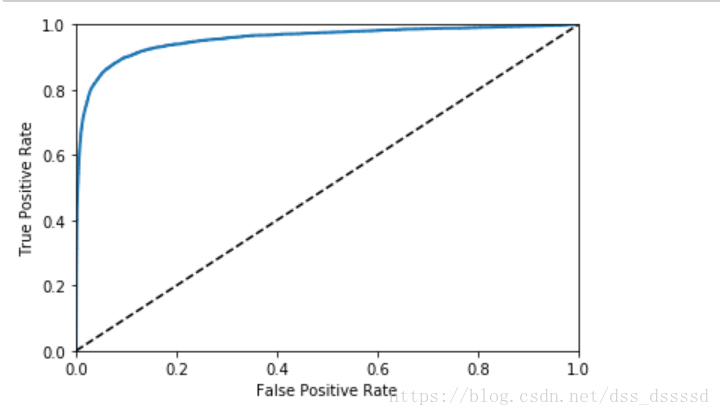
畫 ROC 曲線

def plot_roc_curve(fpr, tpr, label=None):
    plt.plot(fpr, tpr, linewidth=2, label=label)
    plt.plot([0,1], [0,1], 'k--')
    
    plt.axis([0, 1, 0, 1])
    plt.xlabel("False Positive Rate")
    plt.ylabel("True Positive Rate")

plot_roc_curve(fpr, tpr)

在圖中仍然看出tradeoff, 隨著recall（TPR）的升高，分類器產生更多的false positive（FPR），虛線代表的是純隨機分類器（purely random classifier），一個好的分類器永遠儘可能的遠離虛線，儘可能的靠近左上角

AUC

一種類比較分類器好壞的方法是測量AUC(area under the curve),一個完美的分類器AUC = 1，一個純隨機分類的AUC=0.5，可以使用roc_auc_score來計算AUC的值

from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_scores)

out:

0.956021054307335

既然ROC和PR曲線類似，那使用哪一個呢？

經驗法則是，當正樣本很少，或者更關心false positives（預測結果將多少負樣本預測為正樣本） 而非false negatives（預測結果將多少正樣本預測為負樣本）使用PR， 否則使用ROC。

比如從ROC曲線可以看出分類器表現已經很好，那是因為5的種類要遠少於non-5 ，而從PR曲線卻可以看出，分類器還可以提升，更加靠近右上角

RandomFroestClassifier

接下來訓練一個隨機森林的分類器（RandomFroestClassifier），與SGDClassifier比較一下

from sklearn.ensemble import RandomForestClassifier

forest_clf = RandomForestClassifier(random_state=42)
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3,
                                   method="predict_proba")

RandonForestClassifier 並沒有decision_function()函式，有一個predict_proba()函式，返回的是二維陣列，每一個樣本為一行，預測的類別為列，每一列中數值為該樣本預測屬於該類別的概率

前5個樣本的概率， 第一列為non-5， 第二列為5

y_probas_forest[:5]    

out:

array([[1. , 0. ],
[0.9, 0.1],
[1. , 0. ],
[1. , 0. ],
[1. , 0. ]])

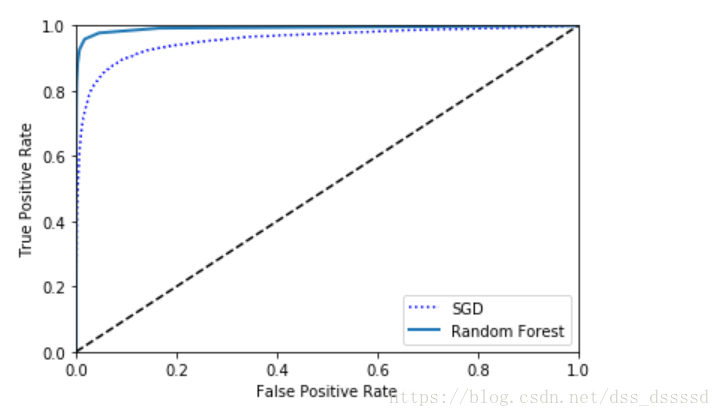
畫ROC曲線

要畫曲線，需要分數，而非概率，簡單的，可以是使用每個例項為5的概率作為分數

y_scores_forest = y_probas_forest[:, 1]
fpr_forest, tpr_forest, threshold_fprest = roc_curve(y_train_5, y_scores_forest)

# 畫
plt.plot(fpr, tpr, "b:", label="SGD")
plot_roc_curve(fpr_forest, tpr_forest, "Random Forest")
plt.legend(loc="lower right")

從圖中看出，隨機森林分類器的表現效能更好一點。

AUC得分

roc_auc_score(y_train_5, y_scores_forest)

out:

0.9924050155627879

計算precision和recall

#大於0.5為True， 否則為False
# import numpy as np

# a = np.array([0, 1, 0.7, 0.2])
# a = a > 0.5
# a

y_scores_forest_pred = y_scores_forest > 0.5
precision_score(y_train_5, y_scores_forest_pred)
recall_score(y_train_5, y_scores_forest_pred)

out：

0.9856891237340378
0.8258623870134661

可以看出大約98.5%的precision， 82.8%的recall,模型的表現不算錯

三、 Multiclass Classification

至於多類分類器，可以使用Random Forest classifier或者naive Bayes classifier直接進行多類分類，而至於svm和linear classifier則是二元分類器（binary classifier），當然可以使用多個二元分類器來實現多元分類，以上是一些常用的方法。

• 比如要分類0~9,，可以訓練10個二元分類器，每一個分類器負責分類一個數字，（0-detector， 1-dector， 2-dector），當要識別一個圖片時，利用10個二元分類器預測，分數最高的那個二元分類器就是識別的數字，稱為one-versus-all（OvA）strategy， 也叫one-versus-the-rest

• 另一種策略是為每兩個數字單獨訓練一個二元分類器，比如 0s-1s， 1s-2s，2s-3s，比如要區分N類，則需要 $N \times (N - 1) / 2$個二元分類器。這被稱之為OvO（one-versus-one）strategy， 要分10個數字需要訓練45個二元分類器，當要識別一個手寫字型時， 將影象分別餵給45個分類器，看一下最後45個分類器的輸出結果中哪一個類別佔的數量最多，就是哪一類。優點是對於每一個分類器訓練時，只需要使用訓練集中對應兩個類別的資料就好。

對於一些演算法（svm）其訓練速度及表現會隨著訓練集的增大而迅速變差，因此對於這些演算法，OvO表現的很好，因為相比於在大資料集上訓練分類器，在小資料集上訓練的速度會更快。但是對於大多數二元分類演算法，OvA更好

當使用二元分類演算法分類多元任務時，sklearn會自動使用OvA（當使用svm classifer時，使用OvO方法）

使用SGDClassifier分類器在資料及上訓練

sgd_clf.fit(X_train, y_train)
# 預測
sgd_clf.predict([some_digits])

out:

array([6.])

實際上sklearn訓練了10個二元分類器，得到影象的10個分數，然後分數最高的那個類別是預測結果。
接下來使用decision_function()函式來看一下過程，此時返回的是10個分數

some_digits_scores = sgd_clf.decision_function([some_digits])
some_digits_scores

out:

array([[-595663.21955387, -877340.07369729, -97322.79677218,
-775219.39150077, -187594.85072678, -413834.30335973,
549962.55145472, -604738.90260495, -793937.08372435,
-588881.53014329]])

注意： 當一個分類器在訓練時，在class_屬性中儲存類別的列表，按照值有小到大排序

pos = np.argmax(some_digits_sc