SLS機器學習介紹(02):時序聚類建模
文章系列連結
前言
第一篇文章SLS機器學習介紹(01):時序統計建模上週更新完,一下子炸出了很多潛伏的業內高手,忽的發現集團內部各個業務線都針對時序分析存在一定的需求。大傢俬信問我業務線上的具體方法,在此針對遇到的通用問題予以陳述(權且拋磚引玉,希望各位大牛提供更好的建議和方法):
-
資料的高頻抖動如何處理?
- 在業務需求能滿足的條件下,進可能的對資料做聚合操作,用視窗策略消除抖動
- 若不能粗粒度的聚合,我一般會選擇視窗濾波操作,在針對濾波後的資料進行一次去異常點操作
- 改變檢測策略,將問題變成一個迴歸問題,引入多維度特徵,對目標進行預測
-
歷史訓練資料如何選擇?
- 針對自己的時序資料,需要先進行簡單的摸底操作,選擇合適的模型,是不是有明顯的週期?是不是有明顯的趨勢?
-
這麼多方法該如何選擇?
- 針對單指標預測的方法,需要採用多種演算法模型進行預測,將得到的結果也要整合起來,降低誤報操作
- 可以針對歷史上的全量報警樣本,設計一套報警聚合規則,在一定容忍度的條件下得到較好的結果
摘要
在大型網際網路企業中,對海量KPI(關鍵效能指標)進行監控和異常檢測是確保服務質量和可靠性的重要手段。基於網際網路的服務型企業(如線上購物、社交網路、搜尋引擎等)通過監控各種系統及應用的數以萬計的KPI(如CPU利用率、每秒請求量等)來確保服務可靠性。KPI上的異常通常反映了其相關應用上可能出現故障,如伺服器故障、網路負載過高、外部攻擊等。因而,異常檢測技術被廣泛用於及時檢測異常事件以達到快速止損的目的。
問題背景
大多數異常檢測演算法(如雅虎的EDAGS,Twitter的BreakoutDetection,FaceBook的prophet)都需要為每條KPI單獨建立異常檢測模型,在面對海量KPI時,會產生極大的模型選擇、引數調優、模型訓練及異常標註開銷。幸運的是,由於許多KPI之間存在隱含的關聯性,它們是較為相似的。如果我們能夠找到這些相似的KPI(例如在一個負載均衡的伺服器叢集中每個伺服器上的每秒請求量KPI是相似的),將它們劃分為若干聚類簇,則可以在每個聚類簇中應用相同的異常檢測模型,從而大大降低各項開銷。
序列聚類建模
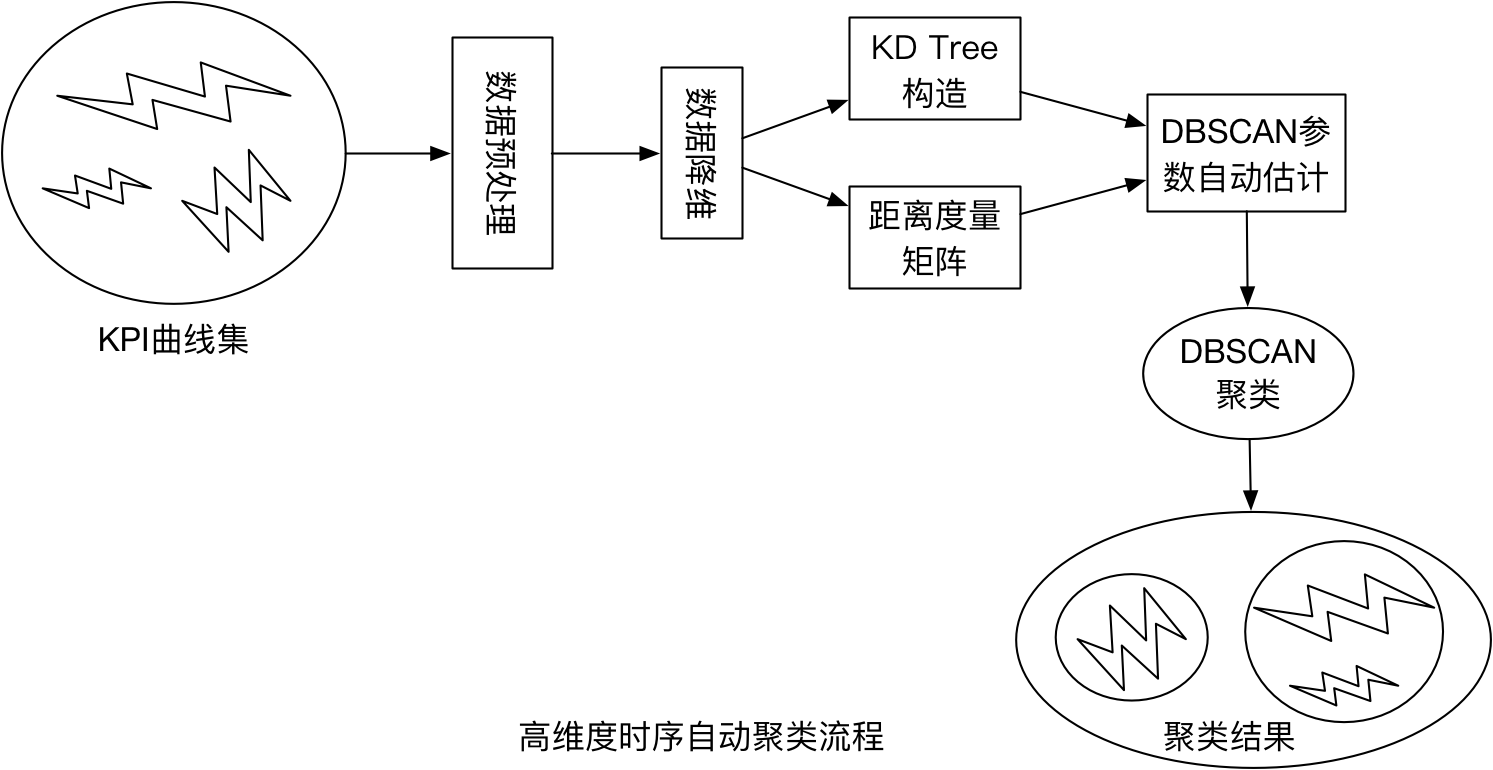
問題定義
在同一個業務指標的前提下:
- 查找出當前時序序列中有哪些相似的曲線形態?(單條曲線的多形態分解)
- 多條KPI指標曲線有哪些曲線的形態類似?(N條曲線形態聚類)
相似性度量
本文主要從時間對齊的多條時序KPI中進行相似性度量,時間點上的指標的相似性和時序曲線形態的相似性
- 時間點聚類(時間上的相似性)
1.1 閔可夫斯基距離:衡量數值點之間距離的一種常見的方法,假設$P=(x_1,x_2,...,x_n)$和$Q=(y_1,y_2,...,y_n)$,則具體的公式如下:
$$ dist = (\sum_{i=1}^{n}|x_i-y_i|^p)^{\frac{1}{p}} $$
當$p=1$時,表示曼哈頓距離;$p=2$時,表示歐幾里得距離;當p趨近於無窮大時,該距離轉換為切比雪夫距離,具體如下式所式:
$$ \lim_{p->\infty}(\sum_{i=1}^{n}|x_i-y_i|^p)^{\frac{1}{p}} = max_{i=1}^{n}|x_i-y_i| $$
閔可夫斯基距離比較直觀,但是它與資料的分佈無關,具有一定的侷限性,如果x方向的幅值遠遠大於y方向的幅值,這個距離公式就會過度方法x維度的作用。因此在加算前,需要對資料進行變換(去均值,除以標準差)。這種方法在假設資料各個維度不相關的情況下,利用資料分佈的特性計算出不同的距離。如果資料維度之間資料相關,這時該類距離就不合適了!
1.2 馬氏距離:若不同維度之間存在相關性和尺度變換等關係,需要使用一種變化規則,將當前空間中的向量變換到另一個可以簡單度量的空間中去測量。假設樣本之間的協方差矩陣是$\Sigma$,利用矩陣分解(LU分解)可以轉換為下三角矩陣和上三角矩陣的乘積:$\Sigma=LL^T$。消除不同維度之間的相關性和尺度變換,需要對樣本x做如下處理:$z=L^{-1}(x-\mu)$,經過處理的向量就可以利用歐式距離進行度量。
$$ dist = z^Tz = (x-\mu)^T\Sigma^{-1}(x-\mu) $$
- 形狀之間的相似性(空間上的結構相似性)
2.1 編輯距離
如何去比較兩個不同長度的字串的相似性?給定兩個字串,由一個轉成另一個所需要的最小編輯操作,其中需要有三個操作,相同位置字元的替換、對字串中某個位置進行插入與刪除。具體的遞迴表示式如下:
$$ dp[i][j] = \begin{cases} 0 & i=0,j = 0 \\ j & i=0,j>0 \\ i & i>0,j=0 \\ min(dp[i][j-1] + 1, dp[i-1][j] + 1, dp[i-1][j-1]) & S_1(i) = S_2(j) \\ min(dp[i][j-1] + 1, dp[i-1][j] + 1, dp[i-1][j-1] + 1) & S_1(i) \neq S_2(j) \end{cases} $$
2.2 DTW(Dynamic Time Warpping)距離
動態時間規整(Dynamic Time Warping;DTW)是一種將時間規整和距離測度相結合的一種非線性規整技術。主要思想是把未知量均勻地伸長或者縮短,直到與參考模式的長度一致,在這一過程中,未知量的時間軸要不均勻地扭曲或彎折,以使其特徵與參考模式特徵對正。
DTW(Dynamic Time Warping)距離的計算過程如下:
假設,兩個時間序列Q和C,Q={$q_1$,$q_2$,…,$q_n$},C={$c_1$,$c_2$,…,$c_m$}。構造一個(n, m)的矩陣,第(i, j)單元記錄兩個點$(q_i,c_j)$之間的歐氏距離,$d(q_i,c_j )=|q_i-c_j |$。一條彎折的路徑W,由若干個彼此相連的矩陣單元構成,這條路徑描述了Q和C之間的一種對映。設第k個單元定義為$w_k=(i,j)_k$,則$w=\{w_1, w_2, w_3, ..., w_K\}, max(n,m) <= K <= n+m-1$。
這條彎折的路徑滿足如下的條件:
1. 邊界條件:$w_1=(1,1)$,且$w_k=(n,m)$
2. 連續性:設$w_k=(a, b)$,$w_{k-1}=(a^{'}, b^{'})$,那麼$a-a^{'}<= 1$,$b-b^{'}<=1$
3. 單調性:設$w_k=(a,b)$,$w_{k-1}=(a^{'}, b^{'})$,那麼$a-a^{'}>=0, b-b^{'} >=0$
在滿足上述條件的多條路徑中,最短的,花費最少的一條路徑是:
$$ DTW(Q,C) = min\{1/K \sqrt(\sum_{k=1}^{K}w_k)\} $$
DTW距離的計算過程是一個DP過程,先用歐式距離初始化矩陣,然後使用如下遞推公式進行求解:
$$ r(i,j) = d(i,j) + min\{r(i-1, j-1), r(i-1, j), r(i, j-1)\} $$
演算法步驟
1. 資料預處理
-
資料來源:叢集中所有叢集的多指標度量值(秒級資料)
- SYS:系統執行情況記錄(啟動時間,負載情況、程序資訊等)
- NET:網路裝置狀態傳輸情況(TCP、UDP等上行和下行流量等)
- MEMORY:記憶體使用情況(使用率、交換分割槽使用情況等)
- CPU/GPU:使用情況
- DISK:磁碟IO情況
-
基本的預處理
- 確定下單條資料的資訊(檢視某機器某指標的情況)
* and metric_name : machine_022_cpu | select stamp, metric_val order by stamp limit 2000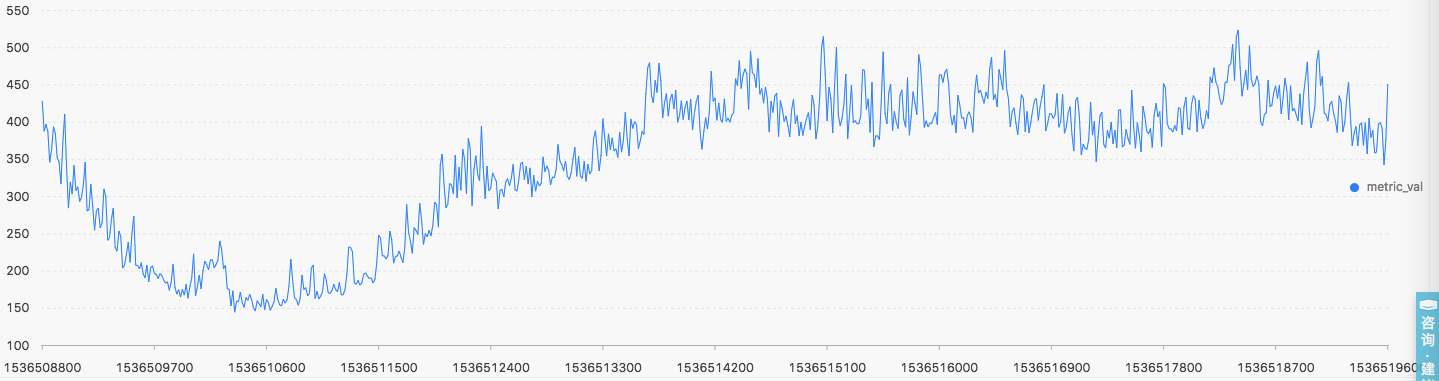
- 若時序資料含有缺失值,需要將將序列進行補點操作(如果序列缺失小於10%,則模型內部會將缺失資料自動按照鄰近值補齊)
- 該資料是按照15秒一個點進行取樣的,如果需要進行更粗粒度的操作,需要額外處理
2. 時序資料的降維取樣
叢集中有相同屬性的機器大約為5K臺,那麼我們就會有經過處理的5K條NET:Tcp的曲線,現在需要對該集合進行聚類,找到其中相似形態的曲線,並發現形態不一致的曲線形態。
- 分段線性表示方法
分段線性表示是一種使用線性模型來對時間序列進行分割的方法,根據不同的分割方法可以使用不同的分割策略來實現,如滑動視窗、自底向上和自頂向下。利用滑動視窗和自底向上方法的時間複雜度為序列長度的平方階, 而自頂向下的時間複雜度為線性階。滑動視窗在一些情況下對時間序列的擬合效果較差,不能很好地反映原時間序列的變化資訊。 - 分段聚合近似(Piecewise Aggregation Approximation,PAA)表示方法
通過對時間序列進行平均分割並利用分段序列的均值來表示原時間序列的方法。 - 符號化表示方法
符號化表示方法是一種將時間序列轉換為字串序列的過程。在時間序列資料探勘過程中,傳統方法主要依賴於定量資料,遠遠不能滿足資料探勘領域中分析和解決問題的要求。在資料結構和演算法設計中,字串具有特定的資料儲存結構以及較為成熟且高效的操作演算法。
![image.png]()
本實驗中將時序序列將高維度資料降低到長度為300的PAA策略。
3. DBSCAN聚類演算法
DBSCAN(Density-BasedSpatial Clustering of Applications with Noise),一種基於密度的聚類方法,即找到被低密度區域分離的稠密區域,要求聚類空間中的一定區域內所包含物件(點或其他空間物件)的數目不小於某一給定閾值。
-
其中幾個關鍵術語:
- 密度:空間中任意一點的密度是以該點為圓心,以Eps為半徑的圓區域內包含的點數目
- 邊界點:空間中某一點的密度,如果小於某一點給定的閾值minPts,則稱為邊界點
- 噪聲點:不屬於核心點,也不屬於邊界點的點,也就是密度為1的點
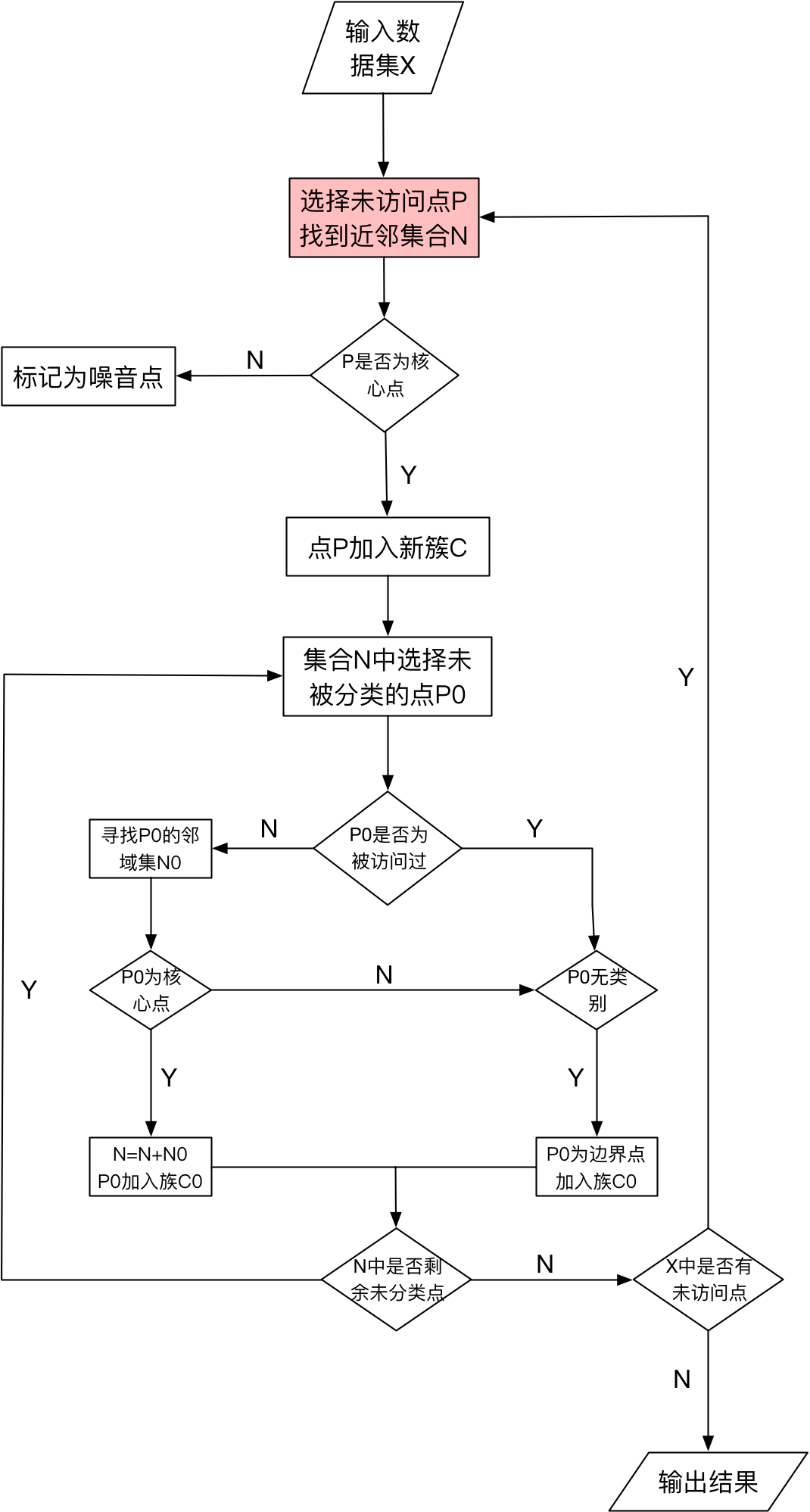
上圖是一般DBSCAN的聚類過程,其中有兩個地方可以進行較好的優化:
-
兩個引數
- 最近兩個聚類中心的距離引數(Eps)
- 最小聚類中心的例項的個數(MinPts)
- 查詢一個向量在給定引數情況下的近鄰集合
3.1 KD Tree構造
KD(K-Dimensional) Tree,是一種分割K維度資料空間的資料結構。主要應用與多維空間關鍵資料的搜尋(如:範圍搜尋和近鄰搜尋)。
function kdtree(list of points pointList, int depth) {
// select axis based on depth so that axis cycles through all valid values
var int axis := depth % k;
// sort point list and choose median as pivot element
select median by axis from pointList;
// create node and construct subtree
node.location := median;
node.leftChild := kdtree(points in pointList before median, depth + 1);
node.rightChild := kdtree(points in pointList before median, depth + 1);
return node;
}上述演算法模型中,最大的問題在於軸點的選擇,選擇好軸點之後,就可以遞迴去建立這顆樹了。
-
建樹必須遵循的兩個準則:
- 建立的樹應當儘量平衡,樹越平衡代表著分割得越平均,搜尋的時間也就是越少;
- 最大化鄰域搜尋的剪枝操作;
-
選擇軸點的策略
- 對於所有描述子資料(特徵向量),統計在每個維度上的資料方差,挑選出方差中最大值,對應的維度就是分割域的值。資料方差大說明沿著該座標軸方向上資料點分散的比較開。這個方向上,進行資料分割可以獲得最好的平衡。資料點集按照當前選擇的維度的值排序,位於正中間的那個資料點,就被選為軸點。
- 實際中會出現問題:理論上空間均勻分佈的點,在一個方向上分割,通過計算方差,下一次分割就不會出現在這個方向上,但實際資料往往會不均勻,這樣就會出現很多長條的分割,會導致效率降低。
- 為了避免這種情況,候選維度的選擇依據是資料範圍最大的那一個維度作為分割維度,之後就選擇這個維度的中間節點作為軸點,進行分割,分割出來的結果會稍微好一些。
- 實際中也可以通過限制樹的高度的時候。
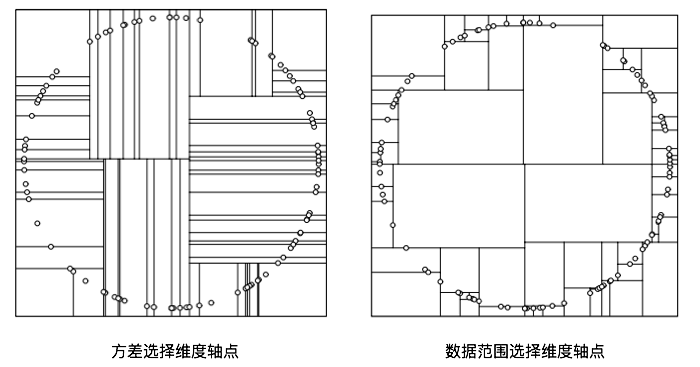
-
鄰近搜尋策略
- 給定一個KD Tree和一個節點,求KD Tree中離這個節點最近的節點,可以選定一個距離度量的方式。
- 搜尋的基本思路:首先通過二叉樹搜尋(比較待查詢節點和分裂節點的分裂維度的值,小於等於就進入左側分支,大於就進入右側分支),順著搜尋路徑很快能找到最近鄰的近似點,也就是與待查詢點處於同一個子空間的葉子節點;然後在回溯搜尋路徑,並判斷搜素路徑上的其它近鄰節點是否有可能距離查詢點更近的資料點,直到搜尋路徑上的候選節點為空時停止。
3.2 引數自動化估計
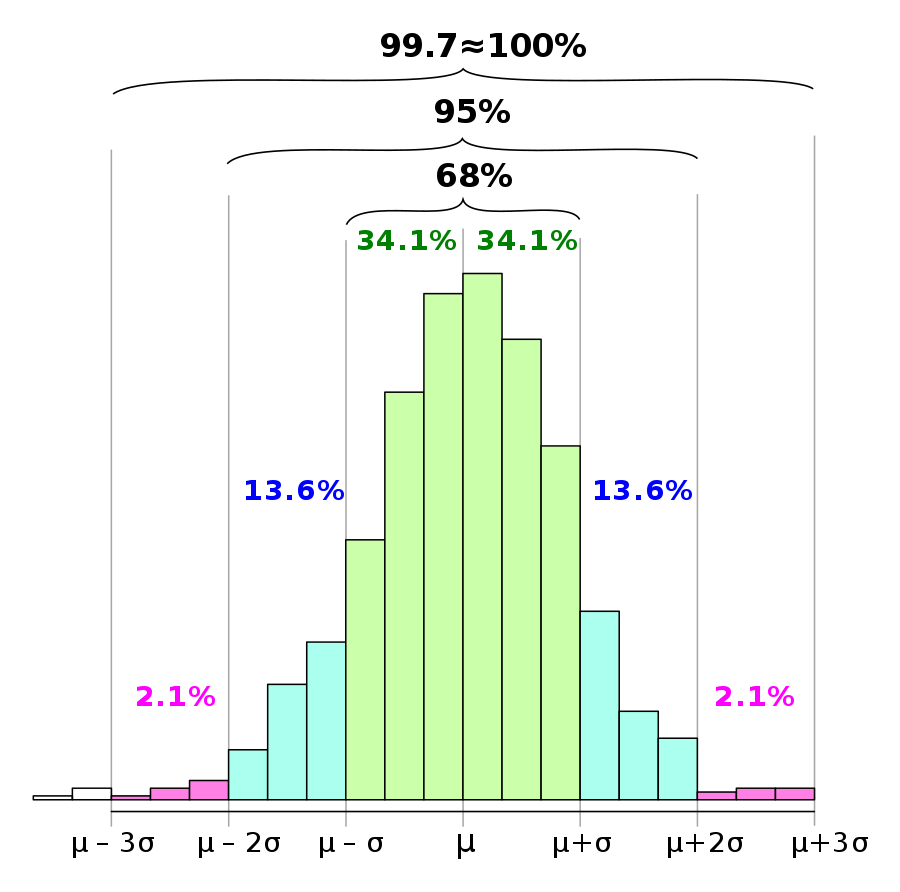
具體的成分如下圖所示:
$$ P(\mu-\sigma \leq X \leq \mu + \sigma) \sim 0.6827 $$
$$ P(\mu-2\sigma \leq X \leq \mu + 2\sigma) \sim 0.9545 $$
$$ P(\mu-3\sigma \leq X \leq \mu + 3\sigma) \sim 0.9973 $$
這裡我們假設$(\mu + 2\sigma, \mu + 3\sigma)$的坐在成分為$2.1%$左右,因此我們假設最小的近鄰集合中所含有的樣本數量為$k=Total Size * 2.1% * 0.5$。
-
具體的引數估計流程如下:
- 計算任意兩個樣本之間的距離
- 計算每個樣本的k-距離值,選擇每個樣本最近鄰的k個樣本,將該所有樣本的k距離集合進行升序排序,同時記錄每個候選距離中對應的點對座標(去重複之後,用來記錄該距離有多少個點)
- 去查詢k距離排序之後的若干波動點(見參考文獻)
- 使用KMeans聚類,對於找到的候選資訊$(eps, minPts)$進行聚類,得到相應的聚類中心
- 然後將該引數送入到DBSCAN中進行聚類,對得到的聚類中心的資訊進行判定,得到較好的聚類結果
3.3 DBSCAN具體流程
直觀的理解下本節開頭關於聚類指標的說明:
- core point:聚類中心向量
- Border Point:某個聚類中心的邊界樣本點
- MinPts:最少聚類中心的樣本點的數量
- $\epsilon$:聚類中心內的最遠邊緣樣本到聚類中心的距離
- Noise Point:噪聲樣本點
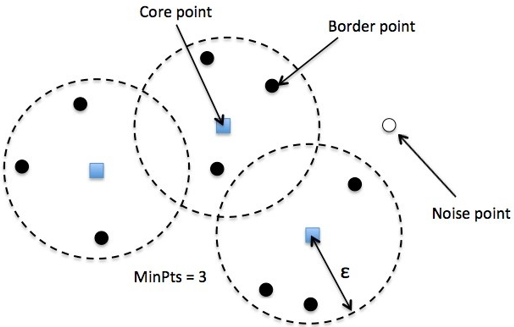
-
DBSCAN演算法描述中常用的概念
- 密度可達:樣本點p,關於樣本點q對於引數${Eps, MinPts}$密度直達,若它滿足$p \in Neighbor(q, Eps)$ 且 $|Neighbor(q, Eps)| >= MinPts$
- 密度可達:樣本點p,關於樣本點q對於引數${Eps, MinPts}$密度可達,若存在一系列的樣本點$p_1,...,p_n$(其中$p_1=q$, $p_n=p$)使得對於$i=1,2...,n-1$,樣本點$p_i$密度可達
- 密度相連:樣本點p,關於樣本點q對於引數${Eps, MinPts}$密度相連,若存在一個樣本點o,使得p和q均由樣本點o密度可達。
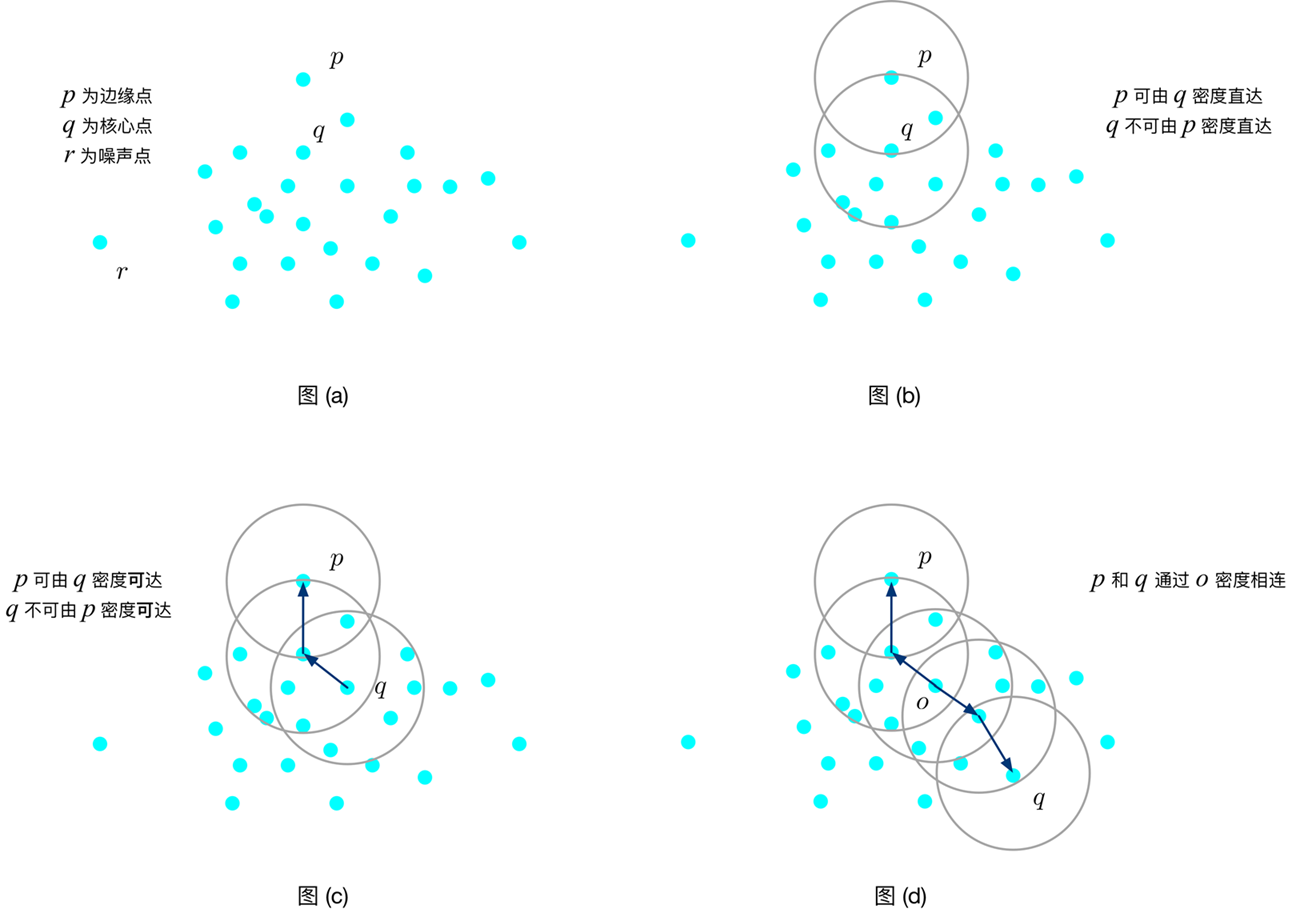
- 具體的演算法流程
首先,將資料集D中的所有物件標記為為處理狀態
for 樣本p in 資料集D do
if p 屬於某個簇 或者 被標記為噪聲 then
continue;
else
檢查p的Eps鄰域 Neighbor(Eps, p)
if |Neighbor(Eps, p)| < MinPts then
標記物件p為邊界點或噪聲點
else
標記樣本p為核心點,並建立新的簇C,並將p鄰域的所有點加入C
for 樣本q in Neighbor(Eps, p)中所有未被處理的物件 do
按照鄰域樣本數量進行判斷
end for
end if
end if
end for4. 層次聚類演算法
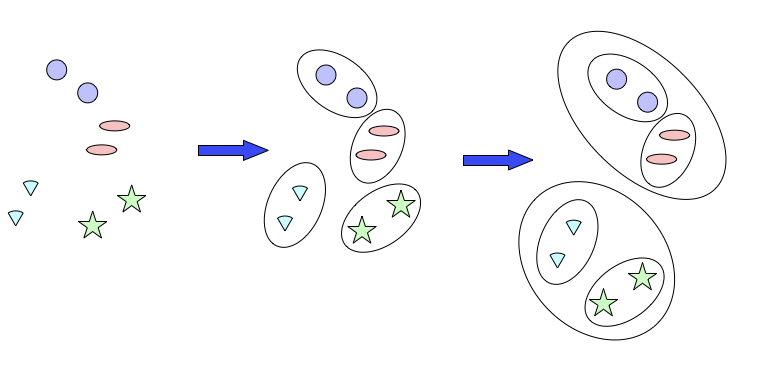
層次聚類是一種很直觀的演算法,就是一層一層的對資料進行聚類操作,可以自低向上進行合併聚類、也可以自頂向下進行分裂聚類。
- 凝聚式:從點作為個體簇開始,每一個步合併兩個最接近的簇
- 分裂式:從包含所有個體的簇開始,每一步分裂一個簇,直到僅剩下單點簇為止
4.1 凝聚層次聚類演算法步驟
- 計算鄰近度量矩陣
-
repeat
- 合併最接近的兩個簇
- 更新鄰近度矩陣,以反映新簇與原來簇之間的鄰近度量值
- Until 僅剩下一個簇或者達到某個終止條件
平臺實驗結果
自動引數選擇的密度聚類演算法
- 呼叫命令
* | select ts_dencity_cluster(stamp, metric_val, metric_name)- 聚類結果
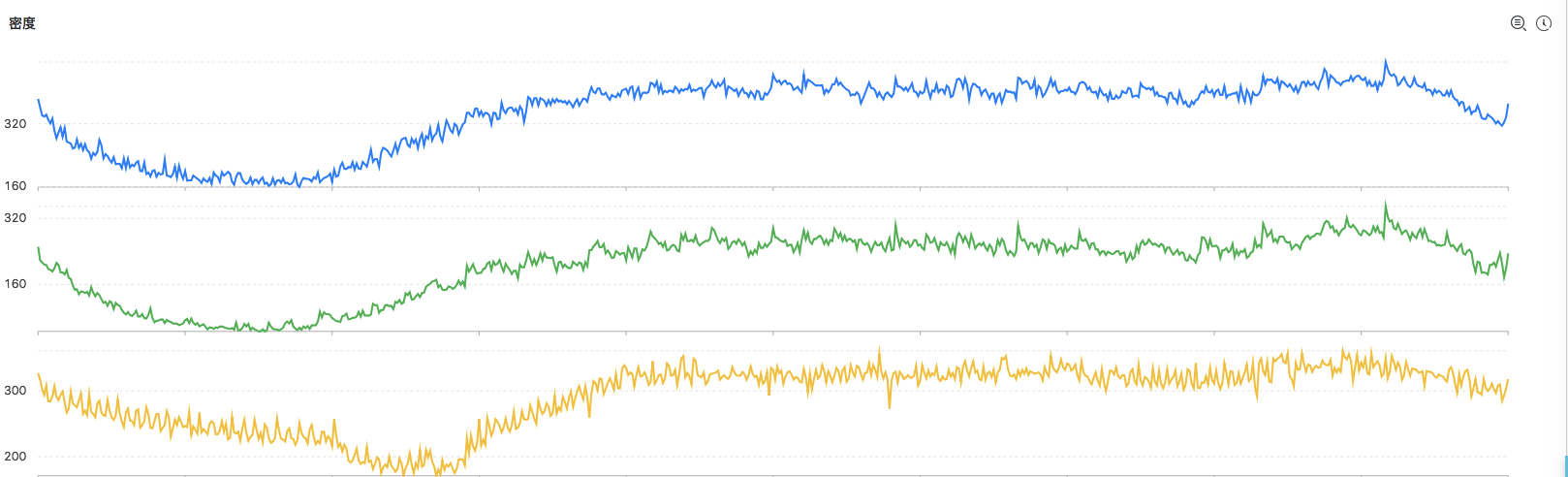
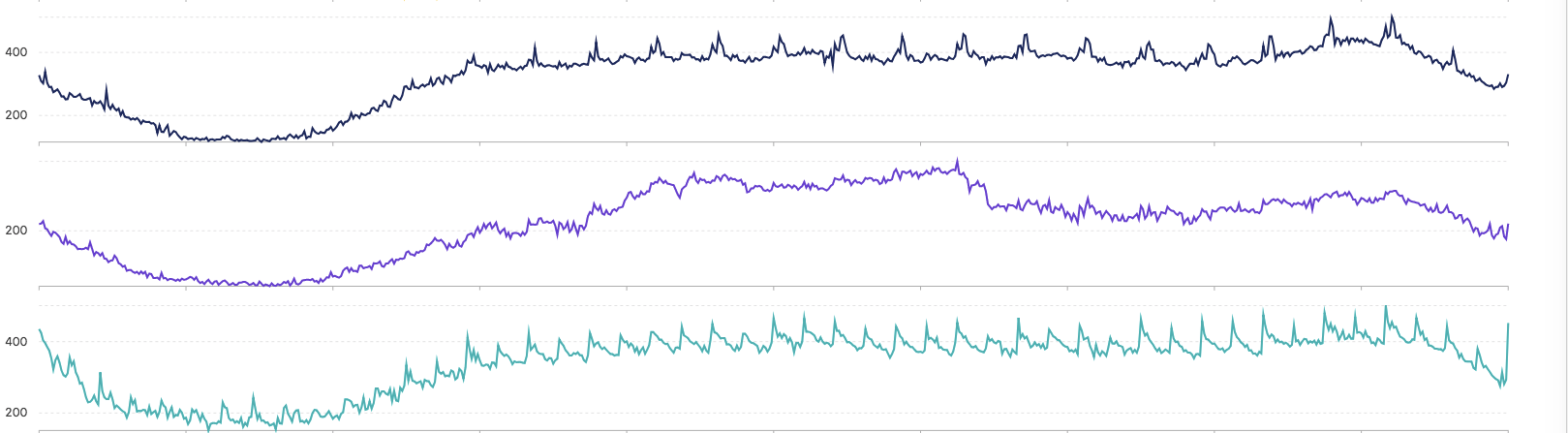
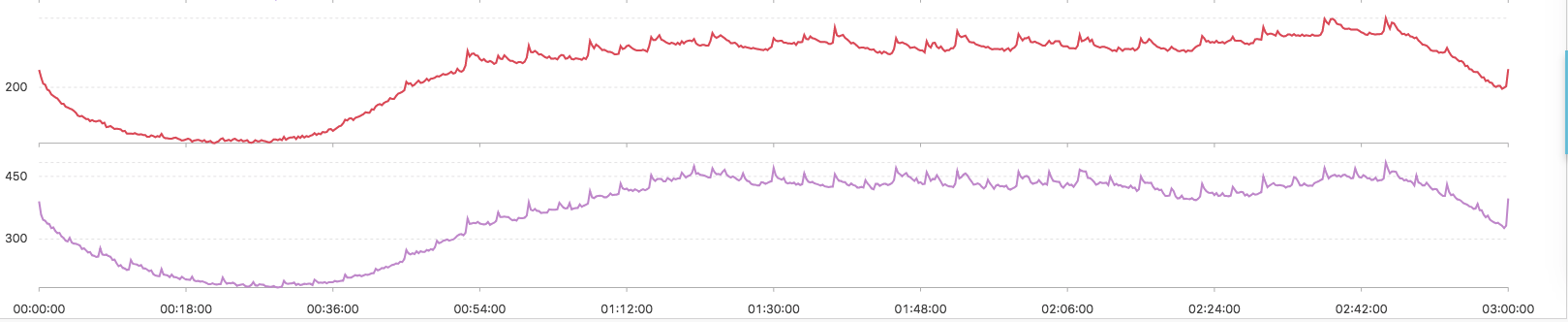
-
上述輸出結果說明
- 聚類的中心的數量有演算法自動生成
- 輸出的結果按照所含有的例項數量降序排列
層次聚類演算法
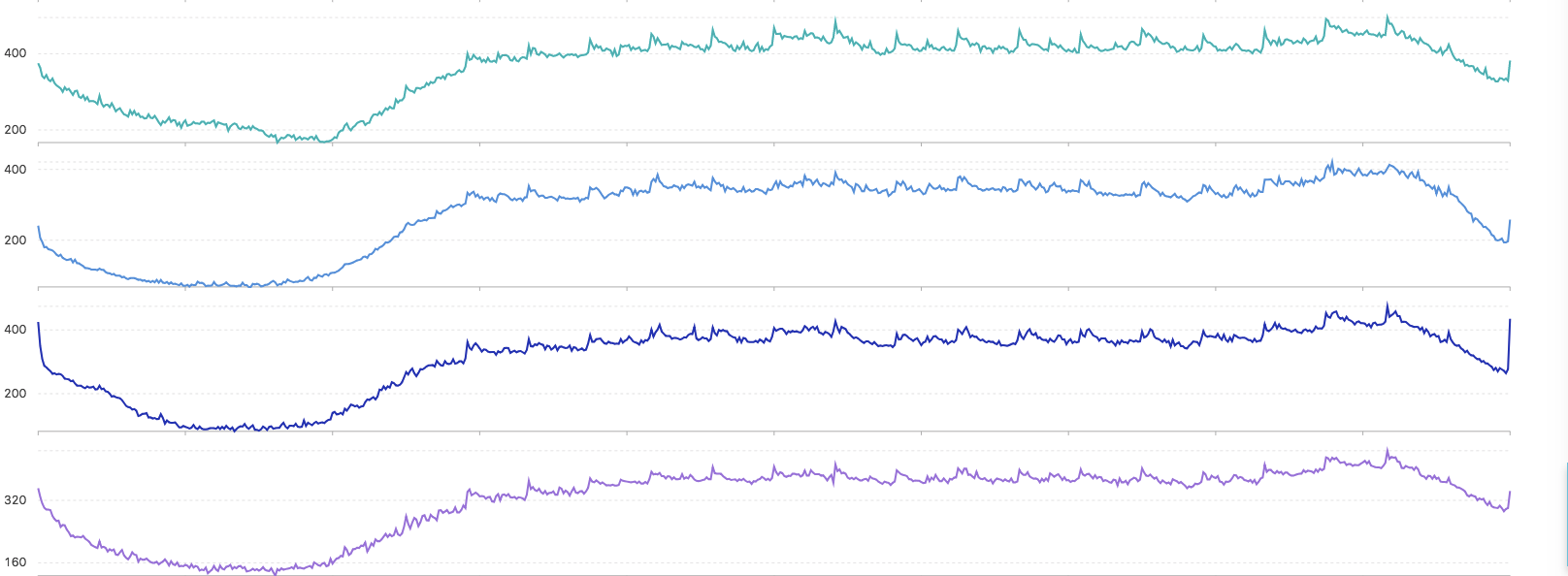
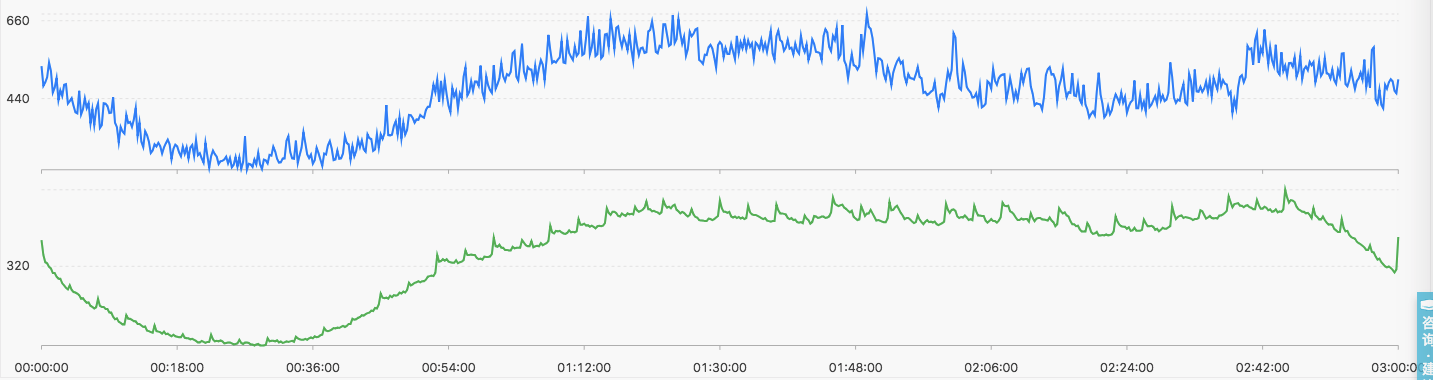
- 呼叫命令
* | select ts_hierarchical_cluster(stamp, metric_val, metric_name, 2)- 聚類結果
- 呼叫命令
* | select ts_hierarchical_cluster(stamp, metric_val, metric_name, 8)- 聚類結果
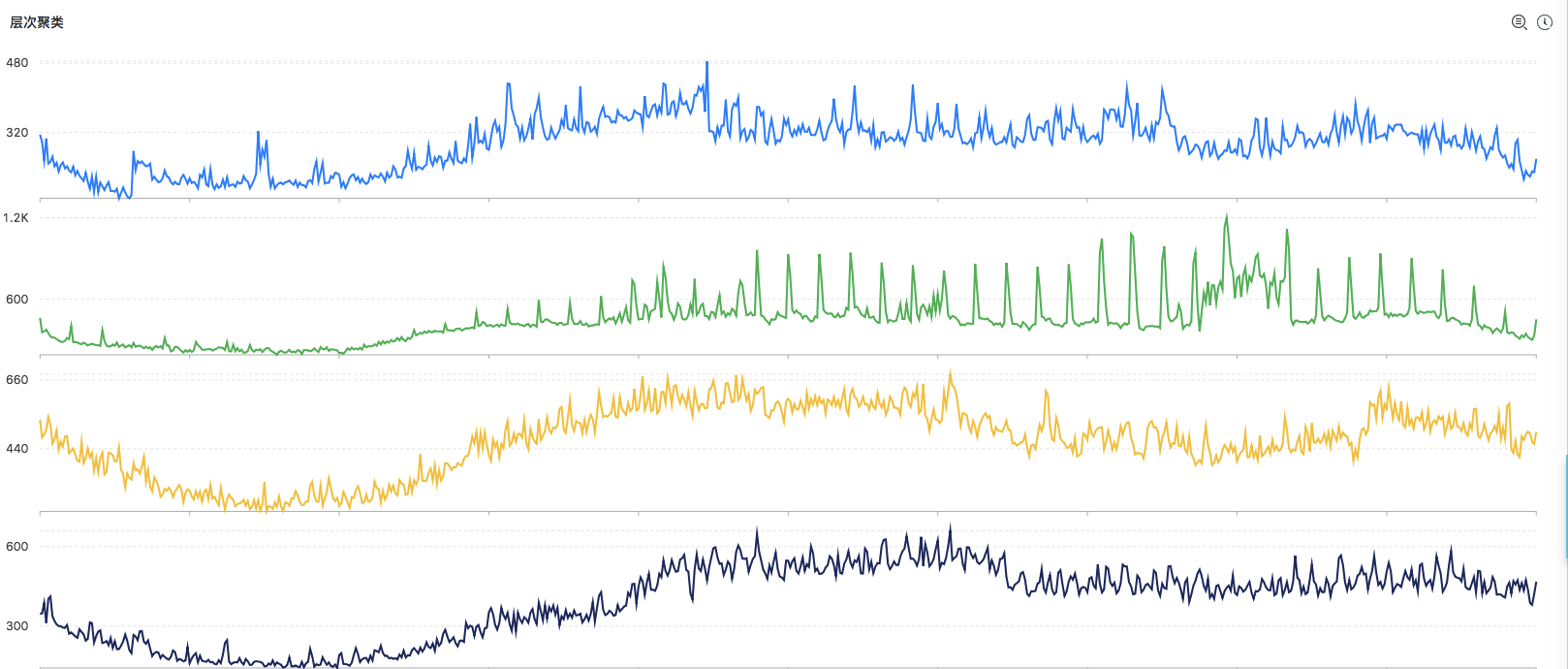
-
上述輸出結果說明
- 聚類的中心的數量的上限使用者可自定義
- 輸出的結果按照所含有的例項數量降序排列
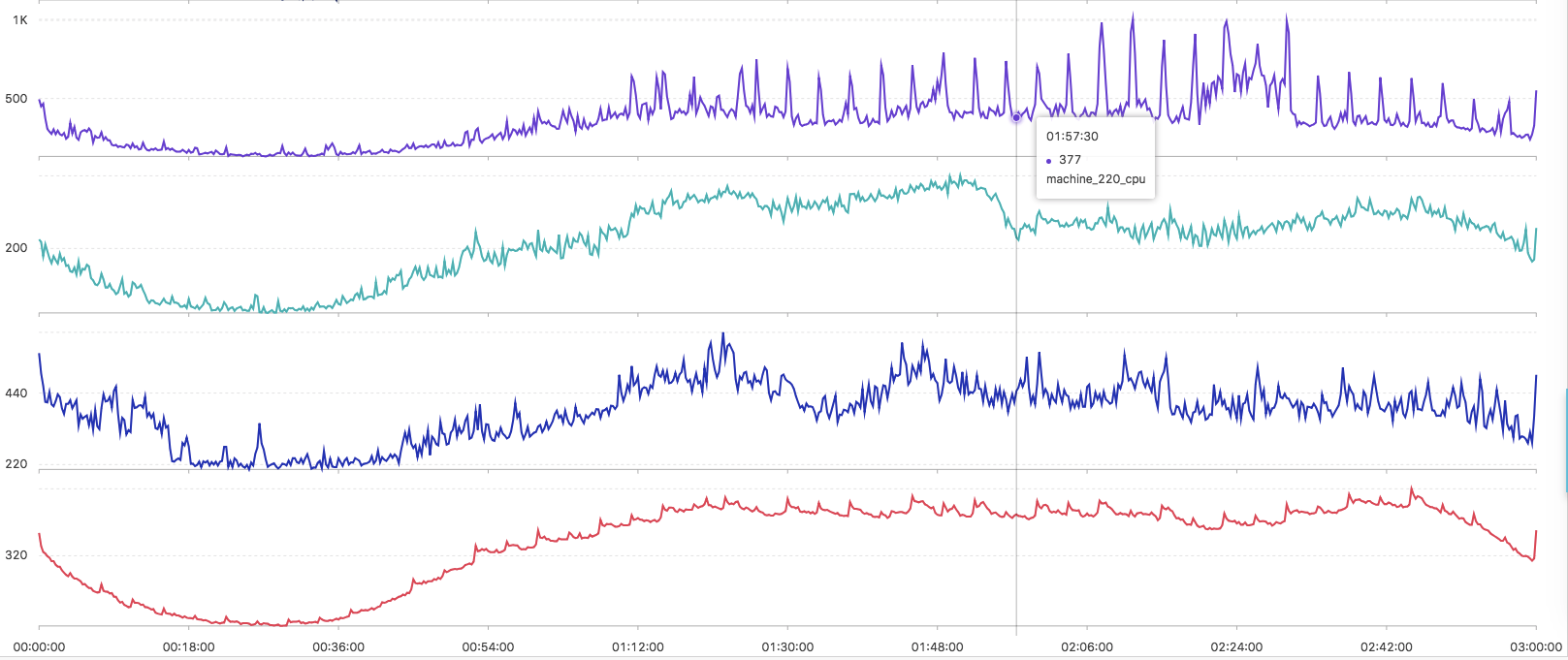
查詢相似曲線
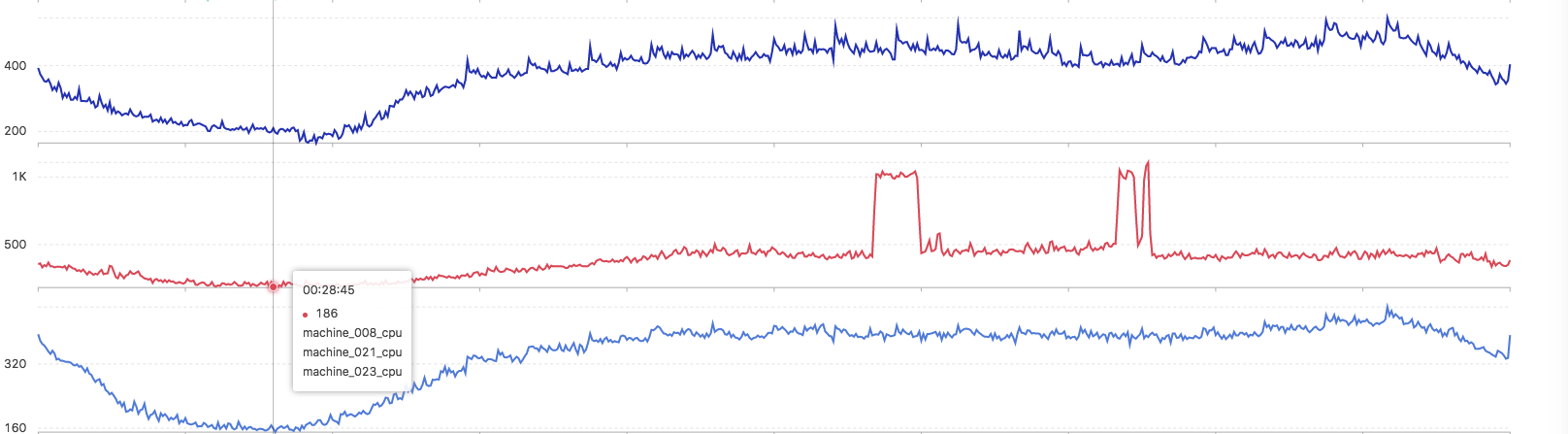
- 呼叫命令
* | select ts_similar_instance(stamp, metric_val, metric_name, 'machine_008_cpu')-
返回結果
- machine_008_cpu
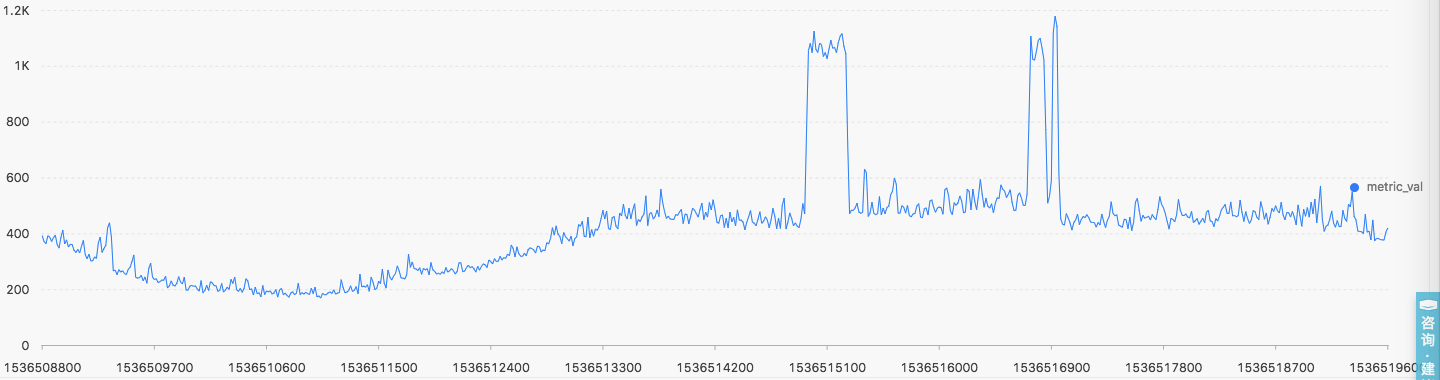
- machine_021_cpu
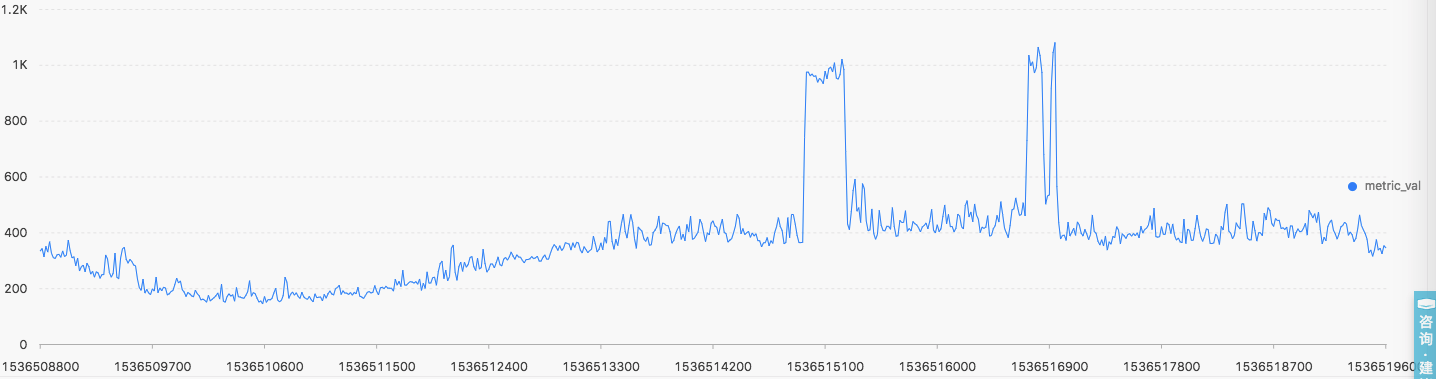
- machine_023_cpu
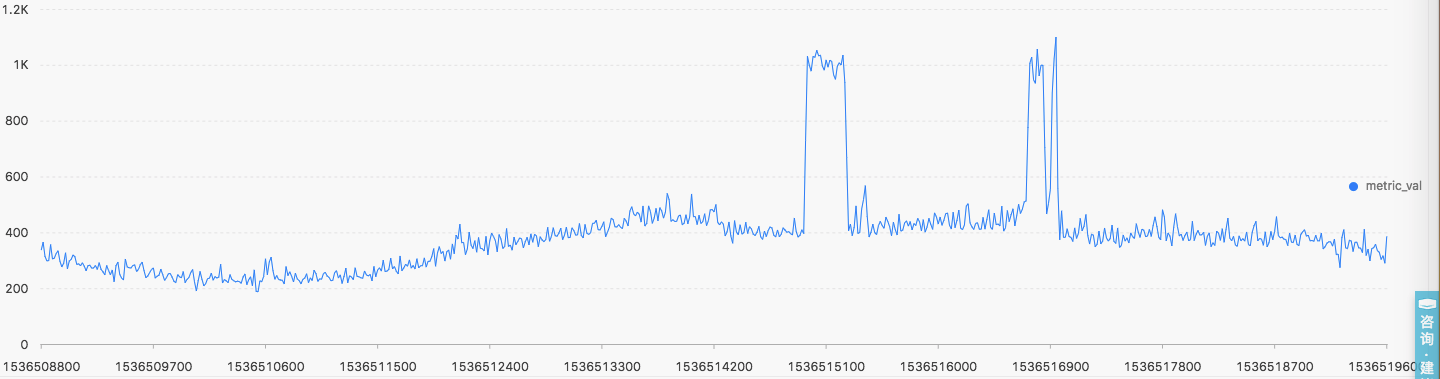
- machine_008_cpu
硬廣時間
日誌進階
阿里雲日誌服務針對日誌提供了完整的解決方案,以下相關功能是日誌進階的必備良藥:
- 機器學習語法與函式:https://help.aliyun.com/document_detail/93024.html
- 日誌上下文查詢:https://help.aliyun.com/document_detail/48148.html
- 快速查詢:https://help.aliyun.com/document_detail/88985.html
- 實時分析:https://help.aliyun.com/document_detail/53608.html
- 快速分析:https://help.aliyun.com/document_detail/66275.html
- 基於日誌設定告警:https://help.aliyun.com/document_detail/48162.html
- 配置大盤:https://help.aliyun.com/document_detail/69313.html
更多日誌進階內容可以參考:日誌服務學習路徑。
聯絡我們
糾錯或者幫助文件以及最佳實踐貢獻,請聯絡:悟冥
問題諮詢請加釘釘群:11775223
Reference
- 微軟亞研院的AIOps底層演算法: KPI快速聚類
- Yading: Fast Clustering of Large-Scale Time Series Data
- 漫談:機器學習中距離和相似性度量方法
- 如何理解K-L散度(相對熵)
- 最小編輯距離演算法
- DTW Algorithm
- A Piecewise Aggregate Approximation Lower-Bound Estimate for Posteriorgram-based Dynamic Time Warping
- 各類降維方法總結
- 68–95–99.7 rule
- Comment on "Clustering by fast search and find of density peaks"
- Clustering by fast search-and-find of density peaks
