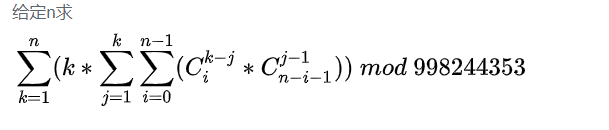
打個暴力查一下OEIS，5min做完

出題人一開始把式子打錯了，一開始的式子的結果為$n * (n + 3) * 2^{n - 3}$

我們考慮化式子

首先考慮

$\sum\limits_{j = 1}^k \sum\limits_{i = 0}^{n - 1} \binom{i}{k- j} * \binom{n - i - 1}{j - 1}$

$= \sum\limits_{i = 0}^{n - 1} \sum\limits_{j = 1}^k \binom{i}{k- j} * \binom{n - i - 1}{j - 1}$

$=  \sum\limits_{i = 0}^{n - 1} \sum\limits_{j = 0}^{k - 1} \binom{i}{k- j - 1} * \binom{n - i - 1}{j}$

我們考慮對後面運用範德蒙德卷積公式$\sum\limits_{i = 0}^k \binom{n}{i} \binom{m}{k - i} = \binom{n + m}{k}$，可以得到

$= \sum\limits_{i = 0}^{n - 1} \binom{n - 1}{k - 1}$

$= n * \binom{n - 1}{k - 1}$

$= k \binom{n}{k}$

因此，原式等於$\sum\limits_{k = 1}^n k^2 \binom{n}{k}$

我們可以對$(1 + x)^n = \sum\limits_{i = 0}^n \binom{n}{i} x^i$連續求導$2$次得到下面的恆等式

$\sum\limits_{k = 1}^n k^2 \binom{n}{k} = n * (n + 1) * 2^{n - 2}$

程式碼實現....算了吧...

複雜度$O(\log n)$