[NOIP2016]憤怒的小鳥（狀壓DP）

阿新 • • 發佈：2018-11-02

[NOIP2016]憤怒的小鳥（狀壓DP）

題目描述

輸入輸出格式

輸入格式：

第一行包含一個正整數 T，表示遊戲的關卡總數。

下面依次輸入這 T個關卡的資訊。每個關卡第一行包含兩個非負整數 n,m，分別表示該關卡中的小豬數量和 Kiana 輸入的神祕指令型別。接下來的 n行中，第 ii 行包含兩個正實數 $xi,yi$ ，表示第 i只小豬座標為 $xi,yi$ 。資料保證同一個關卡中不存在兩隻座標完全相同的小豬。

如果 m=0，表示Kiana輸入了一個沒有任何作用的指令。

如果 m=1，則這個關卡將會滿足：至多用 $\left \lceil n/3+1 \right \rceil$

只小鳥即可消滅所有小豬。

如果 m=2，則這個關卡將會滿足：一定存在一種最優解，其中有一隻小鳥消滅了至少 $\left \lfloor n/3 \right \rfloor$ 只小豬。

保證 $1\leq n\leq 18,0\leq m\leq 2,0<xi,yi<10$

輸出格式：

對每個關卡依次輸出一行答案。

輸出的每一行包含一個正整數，表示相應的關卡中，消滅所有小豬最少需要的小鳥數量。

輸入輸出樣例

輸入樣例#1：

輸出樣例#1：

1
1

輸入樣例#2：

輸出樣例#2:

2
2
3

輸入樣例#3： 複製

輸出樣例#3：

說明

【樣例解釋1】

這組資料中一共有兩個關卡。

第一個關卡與【問題描述】中的情形相同，22只小豬分別位於(1.00,3.00)(1.00,3.00)和 (3.00,3.00)(3.00,3.00)，只需發射一隻飛行軌跡為y = -x^2 + 4xy=−x2+4x的小鳥即可消滅它們。

第二個關卡中有55只小豬，但經過觀察我們可以發現它們的座標都在拋物線 y = -x^2 + 6xy=−x2+6x上，故Kiana只需要發射一隻小鳥即可消滅所有小豬。

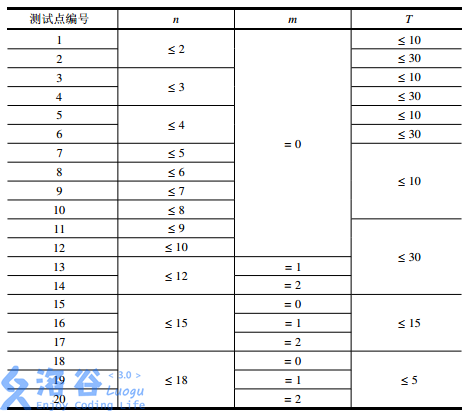
【資料範圍】

Solution

（我們知道三點確定一個拋物線，此處的n<=18）

列舉兩頭豬，設座標為 $(x1,y1),(x2,y2)$ ，以 $(0,0),(x1,y1),(x2,y2)$ 作拋物線，求出拋物線上有哪些豬，記為： $g[i,j]$

於是 $f[i|g[j][k]]=min(f[i|g[j][k]],f[i]+1)$

這顯然是一個 $O(2^{n}n^{2})$ 的做法，似乎不太優秀。

事實上，這個DP有可優化之處：每一次列舉的拋物線必須包含未消滅的第一頭豬！

Because列舉的拋物線的順序與最優解無關，並且未消滅的豬在之後的拋物線中必須被覆蓋到至少一次，那麼與其先覆蓋其他的豬，不如直接先覆蓋第一頭未消滅的豬，這對答案是沒有影響的。因此，每一次轉移只需要列舉能覆蓋第一頭未消滅的豬的拋物線即可。

改變了轉移之後，時間複雜度變為 $O(2^{n}n)$ ，輕鬆AC。

#include <vector>
#include <list>
#include <map>
#include <set>
#include <deque>
#include <queue>
#include <stack>
#include <bitset>
#include <algorithm>
#include <functional>
#include <numeric>
#include <utility>
#include <sstream>
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <cctype>
#include <string>
#include <cstring>
#include <ctime>
#include <cassert>
#include <string.h>
//#include <unordered_set>
//#include <unordered_map>

#define MP(A,B) make_pair(A,B)
#define PB(A) push_back(A)
#define SIZE(A) ((int)A.size())
#define LEN(A) ((int)A.length())
#define FOR(i,a,b) for(int i=(a);i<(b);++i)
#define fi first
#define se second

using namespace std;

template<typename T>inline bool upmin(T &x,T y) { return y<x?x=y,1:0; }
template<typename T>inline bool upmax(T &x,T y) { return x<y?x=y,1:0; }

typedef long long ll;
typedef unsigned long long ull;
typedef long double lod;
typedef pair<int,int> PR;
typedef vector<int> VI;

const lod eps=1e-6;
const lod pi=acos(-1);
const int oo=1<<30;
const ll loo=1ll<<62;
const int mods=1e9+7;
const int MAXN=20;
const int INF=0x3f3f3f3f;//1061109567
/*--------------------------------------------------------------------*/

inline int read() 
{
	int w=0; bool q=1; char c=getchar();
	while ((c<'0'||c>'9')&&c!='-') c=getchar();
	if (c=='-') q=0,c=getchar();
	while (c>='0'&&c<='9') w=w*10+c-'0',c=getchar();
	return q?w:-w;
}

int g[MAXN][MAXN],s[MAXN],f[(1<<MAXN)+5];
double x[MAXN],y[MAXN];
inline bool check(double x,double y){ return abs(x-y)<eps; }
int main(){
    s[0]=1; 
    for (int i=1;i<=19;i++) s[i]=s[i-1]<<1;
    int Case=read();
    while (Case--){
	int n=read(),m=read();
        for (int i=1;i<=n;i++) scanf("%lf%lf",&x[i],&y[i]);
        memset(g,0,sizeof(g));
        memset(f,INF,sizeof(f)); f[0]=0;
        for (int i=1;i<=n;i++)
            for (int j=i+1;j<=n;j++) {
                if (check(x[i],x[j])) continue; double a=(y[j]/x[j]-y[i]/x[i])/(x[j]-x[i]);
                if (a>=0)             continue; double b=y[i]/x[i]-a*x[i];
                for (int k=1;k<=n;k++) g[i][j]+=s[k-1]*(check(a*x[k]+b,y[k]/x[k]));
            }
        for (int i=0;i<=s[n]-1;i++)
            for (int j=1;j<=n;j++)
                if (!(i&s[j-1])){
                    for (int k=j+1;k<=n;k++) upmin(f[i|g[j][k]],f[i]+1);
                    upmin(f[i|s[j-1]],f[i]+1);
                }
        printf("%d\n",f[s[n]-1]);
    }
    return 0;
}

[NOIP2016]憤怒的小鳥（狀壓DP）