20172319 《程式設計與資料結構》 第七週學習總結
阿新 • • 發佈:2018-11-02
20172319 2018.10.27-11.02
《程式設計與資料結構》第7周學習總結
目錄
教材學習內容總結
第十一章 二叉查詢樹
11.1 概述:
- 樹(tree) 是一種非線性 結構,其元素被組織成了一個層次 結構。
- 樹 由一個包含結點 (node) 和邊(edge) 的集構成,其中的元素被儲存在這些結點中,邊則將一個結點和另一個結點連線起來。
- 每一結點都位於該樹層次結構中的某一特定層上。
- 樹的根(root) :即位於該樹頂層 的唯一結點,一棵樹只有一個根結點。
- 位於樹中較低層的結點是上一層結點的孩子(children) , 同一雙親的兩個結點稱為兄弟(sibling) 。
- 沒有任何孩子的結點稱為葉子(leaf) , 一個至少有一個孩子的非根結點 稱為一個內部結點(internal node) 。
- 若某一結點A從根 開始的路徑中位於另一結點B之上,則稱A 為B的祖先(ancestor) , 根是樹中所有結點的最終祖先。
- 沿著起始自某一特定結點的路徑可以到達的結點是該結點的子孫(descendant)。
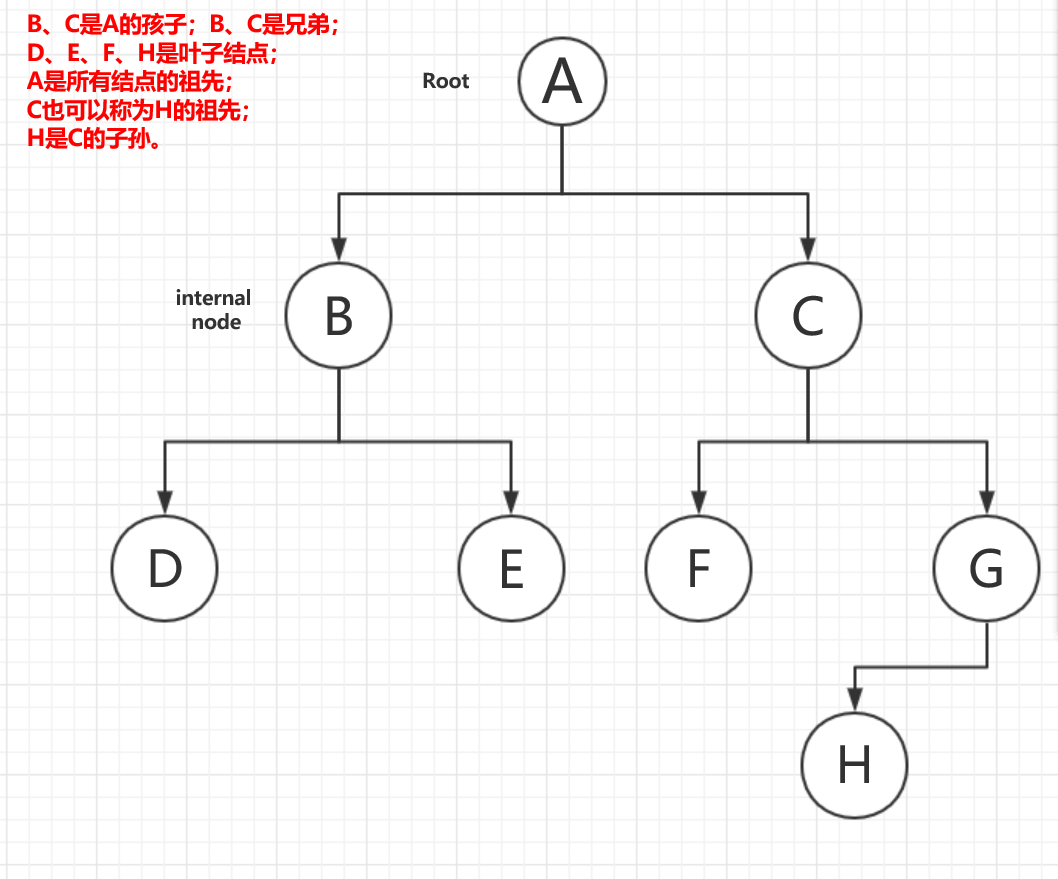
- 結點的層 :從根結點 到該結點的路徑長度。通過計算從根到該結點所必須越過的邊數目,就可以確定其路徑長度(path length) 。
- 樹的高度(height) :指從根到葉子之間最遠路徑的長度。
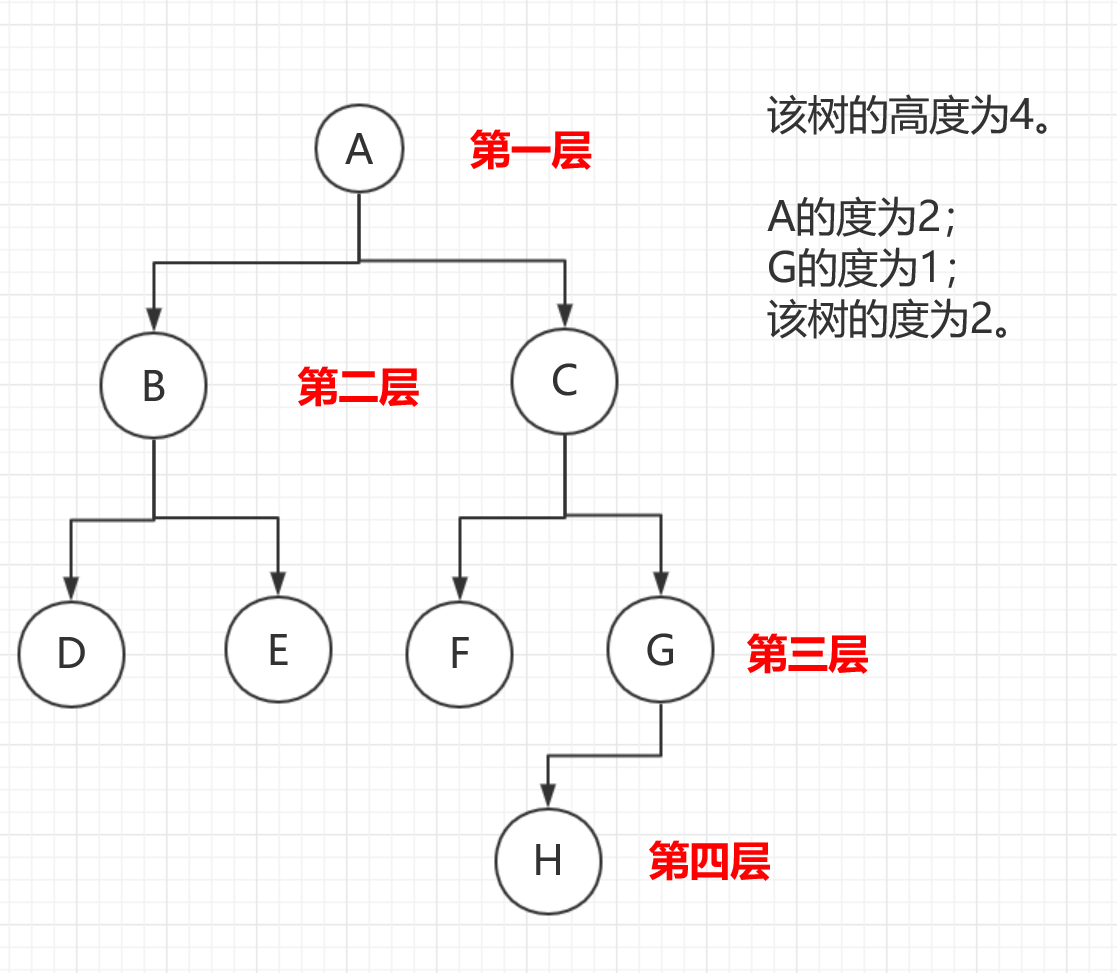
- 10.1.1 樹的分類:
- 分類 方式有很多種:
- 最重要 的一條標準是樹中任一結點可以具有的最大孩子數目。這一值有時候也稱為該樹的度 (order) 。
- 廣義樹(general tree) : 對結點所含有的孩子數目無限制 的樹。
- n元樹(n-ary tree) : 每一結點所含孩子數目不超過n。
- 二叉樹(binary tree) : 結點最多具有兩個孩子。
- 另一種分類方式:
- 判斷該樹是否平衡;粗略地說,如果樹的所有葉子都位於同一層或者至少是彼此相差不超過一層,就稱之為是平衡的。
- 含有m個元素的平衡n元樹具有的高度為lognm。 含有n個結點的平衡二叉樹具有的高度為log2m。
- 完全樹(complete tree) : 如果一棵樹是平衡的,且底層所有葉子都位於樹的左邊,則認為該樹完全。
- 完全二叉樹在每個k層上都具有2k個結點,最後一層除外,在最後一層的結點必須是最左邊結點。

滿樹(full tree) : n元樹的所有葉子都位於同一層且每個結點只有一片葉子或正好具有n個孩子。
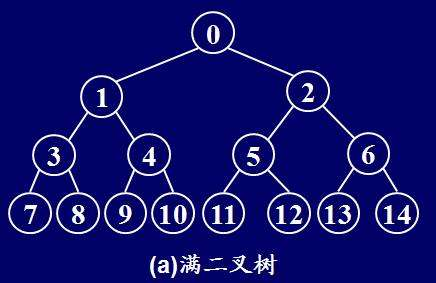
- 11.2 用連結串列實現二叉查詢樹
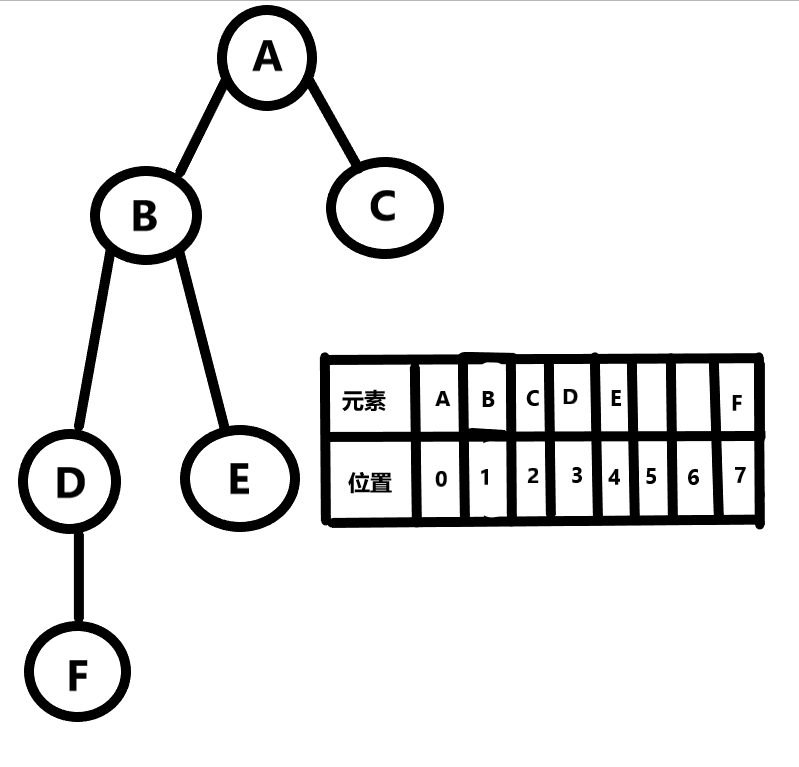
- 10.2.1 樹的陣列實現之計算策略:
- 對於任何儲存在陣列 位置n處的元素而言,該元素的左孩子 將儲存在位置(2 x n +1) 處 ,該元素的右孩子則儲存在位置(2 x (n + 1)) 處。
缺陷 : 浪費儲存空間;其會為不完全樹的無元素位置分配多餘的空間。
- 10.2.2 樹的陣列實現之模擬連結策略:
- 陣列的每一個元素都是一個結點類,每一結點儲存的是每一孩子(可能還有其雙親)的陣列索引,而不是作為指向其孩子(可能還有其雙親)指標的物件引用變數。
- 元素能連續儲存在陣列中,不會浪費儲存空間。
- 增加了刪除樹中元素的成本,要麼對剩餘元素進行移位以維持連續狀態,要麼保留一個空閒列表。
該策略允許連續分配陣列位置而不用考慮該樹的完整性。

- 11.3 用有序列表實現二叉查詢樹
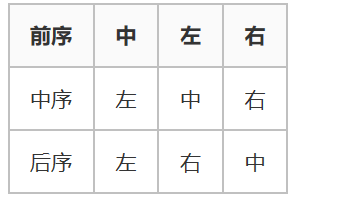
- 10.3.1 前序遍歷(preorder traversal):
- 從根結點開始,訪問每一結點及孩子。

- 10.3.2 中序遍歷(inorder traversal):
從根結點開始,訪問節點的左孩子,然後是該結點,再然後是剩餘任何結點。
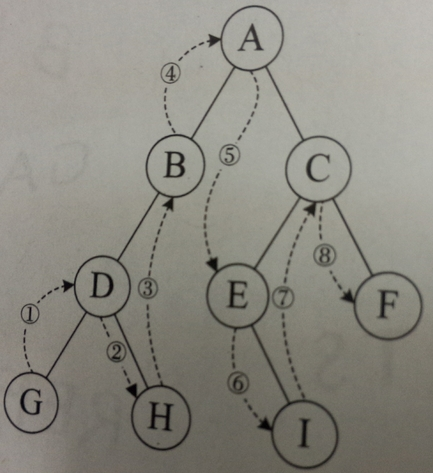
- 10.3.3 後序遍歷(postorder traversal):
從根結點開始,訪問結點的孩子,然後是該結點。

- 10.3.4 層序遍歷(level-order traversal):
從根結點開始,訪問每一層的所有結點,一次一層。

- 11.4 平衡二叉查詢樹
- 二叉樹的操作:
-
操作 說明 getRoot 返回指向二叉樹根的引用 isEmpty 判定該樹是否為空 size 判定樹中的元素數目 contains 判定指定目標是否在樹中 find 如果找到指定元素,則返回指向其引用 toString 返回樹的字串表示 iteratorInOrder 為樹的中序遍歷返回一個迭代器 iteratorPreOrder 為樹的前序遍歷返回一個迭代器 iteratorPostOrder 為樹的後序遍歷返回一個迭代器 iteratorLevelOrder 為樹的層序遍歷返回一個迭代器 11.5 實現二叉查詢樹:AVL樹
11.6 實現二叉查詢樹:紅黑樹
教材學習中的問題和解決過程
- 問題1:無。
- 解決:
程式碼除錯中的問題和解決過程
問題1:如何刪除某一指定結點的子樹。
- 解決:
剛開始的程式碼是:
public LinkedBinaryTree removeRightsubtree(){
LinkedBinaryTree Rightsubtree = new LinkedBinaryTree();
Rightsubtree.root = root;
root.right = null;
return Rightsubtree;
}- 定義一個新二叉樹,將原二叉樹複製,之後將二叉樹根右孩子賦予null,這樣右孩子與其後代便可全部刪除。

- 如果要刪除某一內部結點的子樹怎麼辦?
- 剛開始我寫的方法是這樣的:
public LinkedBinaryTree removeRightsubtree(BinaryTreeNode node){
LinkedBinaryTree Rightsubtree = new LinkedBinaryTree();
Rightsubtree.node = node;
node.right = null;
return Rightsubtree;
}- 然而並不知道具體的元素結點的索引,因此決定換個引數:
public LinkedBinaryTree removeRightsubtree(T Element){
LinkedBinaryTree Rightsubtree = new LinkedBinaryTree();
BinaryTreeNode node = new BinaryTreeNode(Element);
Rightsubtree.node = node;
node.right = null;
return Rightsubtree;
}- 仿造刪除根的子樹的方法,直接給索引結點賦null,然而,node只是我自己新建立的結點,賦值為Element,並非真正想刪除的樹的內部結點。
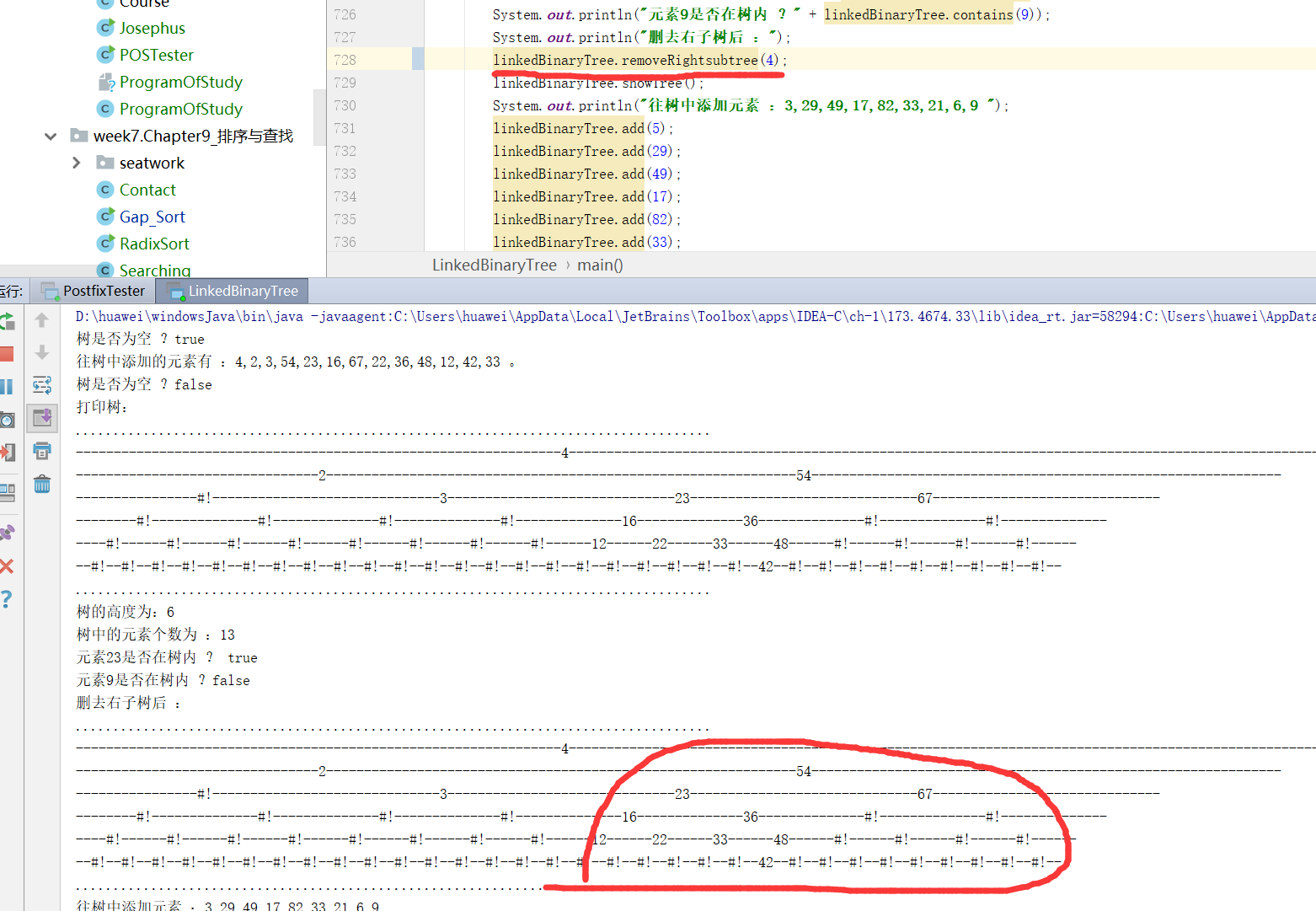
- 顯而易見,沒刪除掉;
- 之後發現首要解決的是找到對應Element元素的位置,然而頭鐵的我剛開始打算自己寫,寫了半天一大堆錯誤之後,才記起有個findNode方法:

- 前面一樣先將原樹複製,後面找到Element所在位置,然後對其子樹進行賦值null,即可刪除。

程式碼託管
上週考試錯題總結
- 錯題1:上週無測試活動。
- 解決:
- 錯題2:
- 解決:
- 錯題3:
- 解決:
結對及互評
點評過的同學部落格和程式碼
- 本週結對學習情況:
- 20172316趙乾宸
- 部落格中值得學習的或存在問題:
- 20172329王文彬
- 部落格中值得學習的或存在問題:
- 部落格內容充實、排版整齊、對教材內容有經過一番認真思考、繼續保持。
- 程式碼截圖做標註時應儘量避免遮擋程式碼。
- Markdown的部分縮排有誤。
- 教材問題2提出得很好,可以看出近斷時間來反覆使用連結串列、陣列去實現同一型別的資料結構起得了一定的成效。
- 20172316趙乾宸
學習進度條
| 程式碼行數(新增/累積) | 部落格量(新增/累積) | 學習時間(新增/累積) | |
|---|---|---|---|
| 目標 | 3000行 | 15篇 | 300小時 |
| 第一週 | 0/0 | 1/1 | 12/12 |
| 第二週 | 935/935 | 1/2 | 24/36 |
| 第三週 | 849/1784 | 1/3 | 34/70 |
| 第四周 | 3600/5384 | 1/5 | 50/120 |
| 第五週 | 2254/7638 | 1/7 | 50/170 |
| 第六週 | 2809/10447 | 1/9 | 45/215 |
參考資料
- ** 樹的定義、分類及儲存 **
- 資料結構及演算法基礎--樹(Tree)(一)基礎詳解
- 【圖解資料結構】 樹
- ** 二叉樹的4種遍歷方法圖解 **
返回目錄
