L1和L2正則化直觀理解
正則化是用於解決模型過擬合的問題。它可以看做是損失函式的懲罰項,即是對模型的引數進行一定的限制。
應用背景:
當模型過於複雜,樣本數不夠多時,模型會對訓練集造成過擬合,模型的泛化能力很差,在測試集上的精度遠低於訓練集。
這時常用正則化來解決過擬合的問題,常用的正則化有L1正則化和L2正則化。
最小平分損失函式的L1正則化:
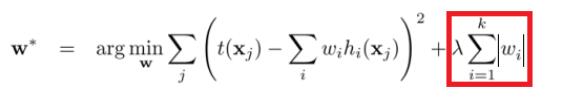
最小平方損失函式的L2正則化:
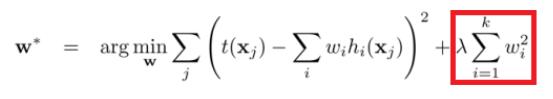
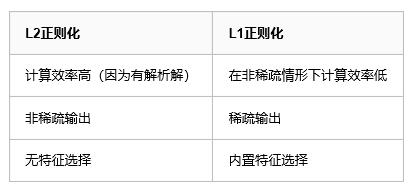
L1正則化與L2正則化的區別:
解的唯一性是一個更簡單的性質,但需要一點想象。首先,看下圖:
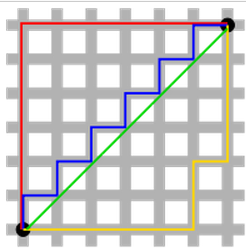
綠色的線(L2範數)是唯一的最短的路徑,而紅色、藍色、黃色線條(L1範數)都是同一路徑,長度一樣(12)。可以將其擴充套件至n-維的情形。這就是為什麼L2範數有唯一解而L1並不是。
內建特徵選擇是L1範數被經常提及的有用的性質,而L2範數並不具備。這是L1範數的自然結果,它趨向於產生稀疏的係數(在後面會解釋)。假設模型有100個係數,但是僅僅只有其中的10個是非零的,這實際上是說“其餘的90個係數在預測目標值時都是無用的”。L2範數產生非稀疏的係數,因此它不具備這個性質。
計算效率。L1範數沒有一個解析解,但是L2範數有。這就允許L2範數在計算上能高效地計算。然而,L1範數的解具備稀疏性,這就允許它可以使用稀疏演算法,以使得計算更加高效
注:解析解是指通過嚴格的公式所求得的解,
例如:方程2y=x
解:
y=0.5x 這是解析解
x=1時,y=0.5 數值解
L1正則化的直觀理解
L1正則化(數學符號表示為 )的公式:在原有的損失函式基礎上加上權重引數的絕對值。 其中 是正則化引數。
中包含了兩部分值,一個是原 ,另一個是 。我們定義 ,這是從幾何上面理解,可以看成是一個正方形。如下圖所述。
藍色的圓代表著原
的損失,圓心代表最佳收斂點,假如沒有正則化的作用,理論上最終會收斂到圓心,但是當存在正則化的作用時,最佳收斂點必須滿足正則化的要求,所以此時的最佳收斂點是正方形與圓的交點。
L1正則化的一個重要特性就是引數稀疏。 對於L1正則化來說,其限定區域為正方形,其與藍色區域(上圖)的交點是頂點的概率很大。也就是說方形的凸點更容易接近
的最優解,而凸點處必有
或
=0,這樣,得到的解
或
為0的概率好大。所以說L1正則化具有稀疏的特性。
L2正則化的直觀理解
L2正則化(數學符號表示為
)的公式:在原有的損失函式基礎上加上權重引數的絕對值。
其中
是正則化引數。
藍色的圓代表著原
的損失,圓心代表最佳收斂點,假如沒有正則化的作用,理論上最終會收斂到圓心,但是當存在正則化的作用時,最佳收斂點必須滿足正則化的要求,所以此時的最佳收斂點是黃色圓與藍色圓的交點。
L2正則化的一個重要特性就是可以獲得很小的引數。 對於L2正則化來說,其限定區域為圓。這樣解的為0的概率很小。
正則化引數
損失函式包含兩個方面:一個是訓練樣本誤差。一個是正則化項。其中,引數 λ 起到了權衡的作用。
以 L2 為例,若 λ 很小,對應上文中的 C 值就很大。這時候,圓形區域很大,能夠讓 w 更接近 最優解的位置。若 λ 近似為 0,相當於圓形區域覆蓋了最優解位置,這時候,正則化失效,容易造成過擬合。相反,若 λ 很大,對應上文中的 C 值就很小。這時候,圓形區域很小,w 離 最優解的位置較遠。w 被限制在一個很小的區域內變化,w 普遍較小且接近 0,起到了正則化的效果。但是,λ 過大容易造成欠擬合。欠擬合和過擬合是兩種對立的狀態。


