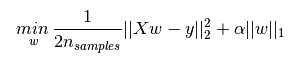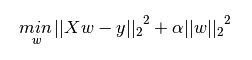理解dropout

from  http://blog.csdn.net/stdcoutzyx/article/details/49022443

• 1
• 2
• 3

開篇明義，dropout是指在深度學習網路的訓練過程中，對於神經網路單元，按照一定的概率將其暫時從網路中丟棄。注意是暫時，對於隨機梯度下降來說，由於是隨機丟棄，故而每一個mini-batch都在訓練不同的網路。

dropout是CNN中防止過擬合提高效果的一個大殺器，但對於其為何有效，卻眾說紛紜。在下讀到兩篇代表性的論文，代表兩種不同的觀點，特此分享給大家。

組合派

參考文獻中第一篇中的觀點，Hinton老大爺提出來的，關於Hinton在深度學習界的地位我就不再贅述了，光是這地位，估計這一派的觀點就是“武當少林”了。注意，派名是我自己起的，各位勿笑。

觀點

該論文從神經網路的難題出發，一步一步引出dropout為何有效的解釋。大規模的神經網路有兩個缺點：

• 費時
• 容易過擬合

這兩個缺點真是抱在深度學習大腿上的兩個大包袱，一左一右，相得益彰，額不，臭氣相投。過擬合是很多機器學習的通病，過擬合了，得到的模型基本就廢了。而為了解決過擬合問題，一般會採用ensemble方法，即訓練多個模型做組合，此時，費時就成為一個大問題，不僅訓練起來費時，測試起來多個模型也很費時。總之，幾乎形成了一個死鎖。

Dropout的出現很好的可以解決這個問題，每次做完dropout，相當於從原始的網路中找到一個更瘦的網路，如下圖所示：

因而，對於一個有N個節點的神經網路，有了dropout後，就可以看做是2n個模型的集合了，但此時要訓練的引數數目卻是不變的，這就解脫了費時的問題。

動機論

雖然直觀上看dropout是ensemble在分類效能上的一個近似，然而實際中，dropout畢竟還是在一個神經網路上進行的，只訓練出了一套模型引數。那麼他到底是因何而有效呢？這就要從動機上進行分析了。論文中作者對dropout的動機做了一個十分精彩的類比：

在自然界中，在中大型動物中，一般是有性繁殖，有性繁殖是指後代的基因從父母兩方各繼承一半。但是從直觀上看，似乎無性繁殖更加合理，因為無性繁殖可以保留大段大段的優秀基因。而有性繁殖則將基因隨機拆了又拆，破壞了大段基因的聯合適應性。

但是自然選擇中畢竟沒有選擇無性繁殖，而選擇了有性繁殖，須知物競天擇，適者生存。我們先做一個假設，那就是基因的力量在於混合的能力而非單個基因的能力。不管是有性繁殖還是無性繁殖都得遵循這個假設。為了證明有性繁殖的強大，我們先看一個概率學小知識。

比如要搞一次恐怖襲擊，兩種方式： 
- 集中50人，讓這50個人密切精準分工，搞一次大爆破。 
- 將50人分成10組，每組5人，分頭行事，去隨便什麼地方搞點動作，成功一次就算。

哪一個成功的概率比較大？ 顯然是後者。因為將一個大團隊作戰變成了游擊戰。

那麼，類比過來，有性繁殖的方式不僅僅可以將優秀的基因傳下來，還可以降低基因之間的聯合適應性，使得複雜的大段大段基因聯合適應性變成比較小的一個一個小段基因的聯合適應性。

dropout也能達到同樣的效果，它強迫一個神經單元，和隨機挑選出來的其他神經單元共同工作，達到好的效果。消除減弱了神經元節點間的聯合適應性，增強了泛化能力。

個人補充一點：那就是植物和微生物大多采用無性繁殖，因為他們的生存環境的變化很小，因而不需要太強的適應新環境的能力，所以保留大段大段優秀的基因適應當前環境就足夠了。而高等動物卻不一樣，要準備隨時適應新的環境，因而將基因之間的聯合適應性變成一個一個小的，更能提高生存的概率。

dropout帶來的模型的變化

而為了達到ensemble的特性，有了dropout後，神經網路的訓練和預測就會發生一些變化。

• 訓練層面

  無可避免的，訓練網路的每個單元要新增一道概率流程。 
  

  對應的公式變化如下如下：

  • 沒有dropout的神經網路 
    
  • 有dropout的神經網路 
    

• 測試層面

  預測的時候，每一個單元的引數要預乘以p。 
  

論文中的其他技術點

• 防止過擬合的方法：

  • 提前終止（當驗證集上的效果變差的時候）
  • L1和L2正則化加權
  • soft weight sharing
  • dropout

• dropout率的選擇

  • 經過交叉驗證，隱含節點dropout率等於0.5的時候效果最好，原因是0.5的時候dropout隨機生成的網路結構最多。
  • dropout也可以被用作一種新增噪聲的方法，直接對input進行操作。輸入層設為更接近1的數。使得輸入變化不會太大（0.8）

• 訓練過程

  • 對引數w的訓練進行球形限制(max-normalization)，對dropout的訓練非常有用。
  • 球形半徑c是一個需要調整的引數。可以使用驗證集進行引數調優
  • dropout自己雖然也很牛，但是dropout、max-normalization、large decaying learning rates and high momentum組合起來效果更好，比如max-norm regularization就可以防止大的learning rate導致的引數blow up。
  • 使用pretraining方法也可以幫助dropout訓練引數，在使用dropout時，要將所有引數都乘以1/p。

• 部分實驗結論

  該論文的實驗部分很豐富，有大量的評測資料。

  • maxout 神經網路中得另一種方法，Cifar-10上超越dropout

  • 文字分類上，dropout效果提升有限，分析原因可能是Reuters-RCV1資料量足夠大，過擬合併不是模型的主要問題

  • dropout與其他standerd regularizers的對比 
    
    • L2 weight decay
    • lasso
    • KL-sparsity
    • max-norm regularization
    • dropout
  • 特徵學習 
    
    • 標準神經網路，節點之間的相關性使得他們可以合作去fix其他節點中得噪聲，但這些合作並不能在unseen data上泛化，於是，過擬合，dropout破壞了這種相關性。在autoencoder上，有dropout的演算法更能學習有意義的特徵（不過只能從直觀上，不能量化）。
    • 產生的向量具有稀疏性。
    • 保持隱含節點數目不變，dropout率變化；保持啟用的隱節點數目不變，隱節點數目變化。
  • 資料量小的時候，dropout效果不好，資料量大了，dropout效果好

  • 模型均值預測

    • 使用weight-scaling來做預測的均值化
    • 使用mente-carlo方法來做預測。即對每個樣本根據dropout率先sample出來k個net，然後做預測，k越大，效果越好。

  • Multiplicative Gaussian Noise 
    使用高斯分佈的dropout而不是伯努利模型dropout

  • dropout的缺點就在於訓練時間是沒有dropout網路的2-3倍。

正則化（Regularization）

機器學習中幾乎都可以看到損失函式後面會新增一個額外項，常用的額外項一般有兩種，一般英文稱作ℓ1-norm和ℓ2-norm，中文稱作L1正則化和L2正則化，或者L1範數和L2範數。

L1正則化和L2正則化可以看做是損失函式的懲罰項。所謂『懲罰』是指對損失函式中的某些引數做一些限制。對於線性迴歸模型，使用L1正則化的模型建叫做Lasso迴歸，使用L2正則化的模型叫做Ridge迴歸（嶺迴歸）。下圖是Python中Lasso迴歸的損失函式，式中加號後面一項α||w||1即為L1正則化項。

下圖是Python中Ridge迴歸的損失函式，式中加號後面一項α||w||22即為L2正則化項。

一般迴歸分析中迴歸w表示特徵的係數，從上式可以看到正則化項是對係數做了處理（限制）。L1正則化和L2正則化的說明如下：

• L1正則化是指權值向量w中各個元素的絕對值之和，通常表示為||w||1
• L2正則化是指權值向量w中各個元素的平方和然後再求平方根（可以看到Ridge迴歸的L2正則化項有平方符號），通常表示為||w||2

一般都會在正則化項之前新增一個係數，Python中用α表示，一些文章也用λ表示。這個係數需要使用者指定。

那新增L1和L2正則化有什麼用？下面是L1正則化和L2正則化的作用，這些表述可以在很多文章中找到。

• L1正則化可以產生稀疏權值矩陣，即產生一個稀疏模型，可以用於特徵選擇
• L2正則化可以防止模型過擬合（overfitting）；一定程度上，L1也可以防止過擬合

稀疏模型與特徵選擇

上面提到L1正則化有助於生成一個稀疏權值矩陣，進而可以用於特徵選擇。為什麼要生成一個稀疏矩陣？

稀疏矩陣指的是很多元素為0，只有少數元素是非零值的矩陣，即得到的線性迴歸模型的大部分系數都是0. 通常機器學習中特徵數量很多，例如文字處理時，如果將一個片語（term）作為一個特徵，那麼特徵數量會達到上萬個（bigram）。在預測或分類時，那麼多特徵顯然難以選擇，但是如果代入這些特徵得到的模型是一個稀疏模型，表示只有少數特徵對這個模型有貢獻，絕大部分特徵是沒有貢獻的，或者貢獻微小（因為它們前面的係數是0或者是很小的值，即使去掉對模型也沒有什麼影響），此時我們就可以只關注係數是非零值的特徵。這就是稀疏模型與特徵選擇的關係。

L1和L2正則化的直觀理解

這部分內容將解釋為什麼L1正則化可以產生稀疏模型（L1是怎麼讓係數等於零的），以及為什麼L2正則化可以防止過擬合。

L1正則化和特徵選擇

假設有如下帶L1正則化的損失函式： 

J=J0+α∑w|w|(1)
其中J0是原始的損失函式，加號後面的一項是L1正則化項，α是正則化係數。注意到L1正則化是權值的絕對值之和，J是帶有絕對值符號的函式，因此J是不完全可微的。機器學習的任務就是要通過一些方法（比如梯度下降）求出損失函式的最小值。當我們在原始損失函式

相關推薦

dropout和L1，L2正則化的理解筆記

理解dropout from http://blog.csdn.net/stdcoutzyx/article/details/49022443 123 開篇明義，dropout是指在深度學習網路的訓練過程中，對於神經網路單元，按照一定的概率將其暫時從網路

L1，L2正則化

正則化引入的思想其實和奧卡姆剃刀原理很相像，奧卡姆剃刀原理：切勿浪費較多東西，去做，用較少的東西，同樣可以做好的事情。 正則化的目的：避免出現過擬合（over-fitting） 經驗風險最小化 + 正則化項 = 結構風險最小化 經驗風險最小化（ERM），是為了讓擬合的誤差足夠小，即：對訓

機器學習筆記（二）L1，L2正則化

2.正則化 2.1 什麼是正則化？ (截自李航《統計學習方法》) 常用的正則項有L1，L2等，這裡只介紹這兩種。 2.2 L1正則項 L1正則，又稱lasso，其公式為： ​ L1=α∑kj=1|θj| 特點：約束θj的大小，並且可以產

機器學習之路： python線性回歸 過擬合 L1與L2正則化

擬合 python sco bsp orm AS score 未知數 spa git：https://github.com/linyi0604/MachineLearning 正則化： 提高模型在未知數據上的泛化能力 避免參數過擬合正則化常用的方法： 在目

l2-loss，l2範數，l2正則化，歐式距離

access src 梯度 com inf content 開平 nbsp alt 歐式距離： l2範數： l2正則化： l2-loss(也叫平方損失函數)： http://openaccess.thecvf.com/content_cvpr_2017/papers

L1與L2正則化

在機器學習中，我們茶廠聽到L1和L2正則化，用他們來防止過擬合，但是在什麼情況下使用它們和它們的原理是什麼樣的可能一知半解。所以在本部落格中將對L1和L2做簡單的介紹和應用場景。 如果引數過多，模型過於複雜，容易造成過擬合（overfit）。即模型在訓練樣本資料上表現的很好

L1、L2正則化

過擬合：對於訓練集擬合效果非常好，但是對於訓練集以外的資料集擬合效果不好。通常發生在變數（特徵）較多的情況，也就是說曲線儘可能的滿足訓練資料集，導致無法泛化（泛化是指模型能夠應用到新樣本的能力）到新資料集中。解決辦法：減少樣本特徵、正則化（通常新增L2正則化） 欠擬合：模型

java手寫邏輯迴歸包括L1，L2正則實現

作為一枚機器學習的愛好者，邏輯迴歸算是一個簡單入門的演算法，原理比較簡單，但是自己手動實現邏輯迴歸有一些要注意的事項： 第一是步長選擇的問題，根據你的資料大小來選擇。 第二是自己手動可選擇加不加入常數項，用於做訓練。 第三是實際寫程式碼用的梯度上升程式碼來求解，演算法原理建

深入剖析迴歸（二）L1，L2正則項，梯度下降

一、迴歸問題的定義 迴歸是監督學習的一個重要問題，迴歸用於預測輸入變數和輸出變數之間的關係。迴歸模型是表示輸入變數到輸出變數之間對映的函式。迴歸問題的學習等價於函式擬合：使用一條函式曲線使其很好的擬合已知函式且很好的預測未知資料。 迴歸問題分為模型的學習和預測兩個

深入理解L1、L2正則化原理與作用

art ida 似的 得來 .net 最優化問題 比較 nor 多維 過節福利，我們來深入理解下L1與L2正則化。 1 正則化的概念 正則化(Regularization) 是機器學習中對原始損失函數引入額外信息，以便防止過擬合和提高模型泛化性能的一類方法的統稱。也就是

L1和L2正則化。L1為什麼能產生稀疏值，L2更平滑

參考部落格：https://zhuanlan.zhihu.com/p/35356992 　　　　　https://zhuanlan.zhihu.com/p/25707761 　　　　　https://www.zhihu.com/question/37096933/answer/70426653 　　首先

L1和L2正則化直觀理解

正則化是用於解決模型過擬合的問題。它可以看做是損失函式的懲罰項，即是對模型的引數進行一定的限制。 應用背景： 當模型過於複雜，樣本數不夠多時，模型會對訓練集造成過擬合，模型的泛化能力很差，在測試集上的精度遠低於訓練集。 這時常用正則化來解決過擬合的問題，常用的正則化有L1正則化和L2

L1正則化和L2正則化

在機器學習中，我們非常關心模型的預測能力，即模型在新資料上的表現，而不希望過擬合現象的的發生，我們通常使用正則化（regularization）技術來防止過擬合情況。正則化是機器學習中通過顯式的控制模型複雜度來避免模型過擬合、確保泛化能力的一種有效方式。如果將模型原始的假設空間比作“天空”，那麼天空飛翔的“鳥

批歸一化（Batch Normalization）、L1正則化和L2正則化

from: https://www.cnblogs.com/skyfsm/p/8453498.html https://www.cnblogs.com/skyfsm/p/8456968.html BN是由Google於2015年提出，這是一個深度神經網路訓練的技巧，它不僅可以加快了

訓練過程--正則化(regularization)技巧(包括L2正則化、dropout，資料增廣，早停)

正則化（regularization）   正則化是解決高方差問題的重要方案之一，也是Reducing Overfiltering（克服過擬合）的方法。   過擬合一直是DeepLearning的大敵，它會導致訓練集的error rate非常小，而測試集的error rate大部分時候很

【通俗易懂】機器學習中 L1 和 L2 正則化的直觀解釋

機器學習中，如果引數過多，模型過於複雜，容易造成過擬合（overfit）。即模型在訓練樣本資料上表現的很好，但在實際測試樣本上表現的較差，不具備良好的泛化能力。為了避免過擬合，最常用的一種方法是使用使用正則化，例如 L1 和 L2 正則化。但是，正則化項是如

L1正則化和L2正則化比較

機器學習監督演算法的基本思路是 讓擬合的模型儘量接近真實資料， 換句更通俗的話, 要讓我們的模型儘量簡單又能很好的反應已知資料之間關係。在這個貼近的過程可能存在兩個截然相反的問題：過擬合和擬合不夠。 擬合不夠是模型預測值與真實值之間誤差較大，上篇文章中提到梯度下降就是討論解決問題（求損失函式最小）。 而正則化

對L1正則化和L2正則化的理解

一、 奧卡姆剃刀(Occam's razor)原理：         在所有可能選擇的模型中，我們應選擇能夠很好的解釋資料，並且十分簡單的模型。從貝葉斯的角度來看，正則項對應於模型的先驗概率。可以假設複雜模型有較小的先驗概率，簡單模型有較大的先驗概率。   二、正則化項   

l1正則化的稀疏表示和l2正則化的協同表示

這些天一直在看稀疏表示和協同表示的相關論文，特此做一個記錄： 這篇文章將主要討論以下的問題： 1.稀疏表示是什麼？ 2.l1正則化對於稀疏表示的幫助是什麼，l0,l1,l2,無窮範數的作用？ 3.稀疏表示的robust為什麼好？ 4.l2正則化的協同表

L1和L2正則化區別

1. L1和L2的定義 L1正則化，又叫Lasso Regression 如下圖所示，L1是向量各元素的絕對值之和 L2正則化，又叫Ridge Regression 如下圖所示，L2是向量各元素的平方和 2. L1和L2的異同點 相同點：都用於避免過擬合 不同點：L