from: https://www.cnblogs.com/skyfsm/p/8453498.html

https://www.cnblogs.com/skyfsm/p/8456968.html

BN是由Google於2015年提出，這是一個深度神經網路訓練的技巧，它不僅可以加快了模型的收斂速度，而且更重要的是在一定程度緩解了深層網路中“梯度彌散”的問題，從而使得訓練深層網路模型更加容易和穩定。所以目前BN已經成為幾乎所有卷積神經網路的標配技巧了。

從字面意思看來Batch Normalization（簡稱BN）就是對每一批資料進行歸一化，確實如此，對於訓練中某一個batch的資料{x1,x2,...,xn}，注意這個資料是可以輸入也可以是網路中間的某一層輸出。在BN出現之前，我們的歸一化操作一般都在資料輸入層，對輸入的資料進行求均值以及求方差做歸一化，但是BN的出現打破了這一個規定，我們可以在網路中任意一層進行歸一化處理，因為我們現在所用的優化方法大多都是min-batch SGD，所以我們的歸一化操作就成為Batch Normalization。

我們為什麼需要BN？

我們知道網路一旦train起來，那麼引數就要發生更新，除了輸入層的資料外(因為輸入層資料，我們已經人為的為每個樣本歸一化)，後面網路每一層的輸入資料分佈是一直在發生變化的，因為在訓練的時候，前面層訓練引數的更新將導致後面層輸入資料分佈的變化。以網路第二層為例：網路的第二層輸入，是由第一層的引數和input計算得到的，而第一層的引數在整個訓練過程中一直在變化，因此必然會引起後面每一層輸入資料分佈的改變。我們把網路中間層在訓練過程中，資料分佈的改變稱之為：“Internal Covariate Shift”。BN的提出，就是要解決在訓練過程中，中間層資料分佈發生改變的情況。

BN怎麼做？

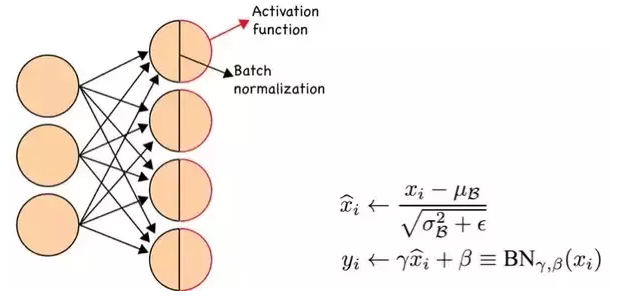
如上圖所示，BN步驟主要分為4步：

1. 求每一個訓練批次資料的均值
2. 求每一個訓練批次資料的方差
3. 使用求得的均值和方差對該批次的訓練資料做歸一化，獲得0-1分佈。其中εε是為了避免除數為0時所使用的微小正數。
4. 尺度變換和偏移：將xixi乘以γγ調整數值大小，再加上ββ增加偏移後得到yiyi，這裡的γγ是尺度因子，ββ是平移因子。這一步是BN的精髓，由於歸一化後的xixi基本會被限制在正態分佈下，使得網路的表達能力下降。為解決該問題，我們引入兩個新的引數：γγ,ββ。 γγ和ββ是在訓練時網路自己學習得到的。

BN到底解決了什麼？

一個標準的歸一化步驟就是減均值除方差，那這種歸一化操作有什麼作用呢？我們觀察下圖，

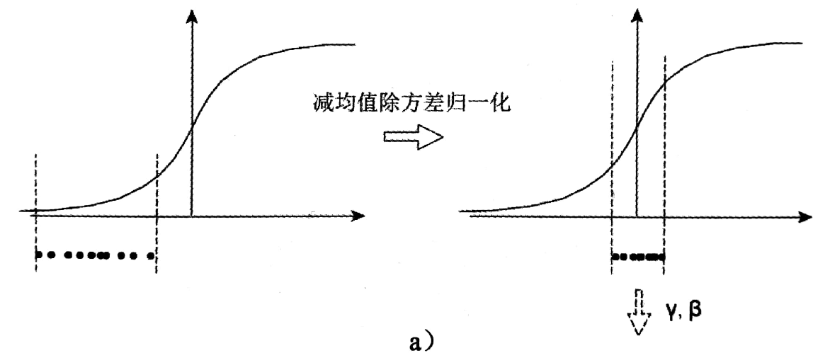
a中左圖是沒有經過任何處理的輸入資料，曲線是sigmoid函式，如果資料在梯度很小的區域，那麼學習率就會很慢甚至陷入長時間的停滯。減均值除方差後，資料就被移到中心區域如右圖所示，對於大多數啟用函式而言，這個區域的梯度都是最大的或者是有梯度的（比如ReLU），這可以看做是一種對抗梯度消失的有效手段。對於一層如此，如果對於每一層資料都那麼做的話，資料的分佈總是在隨著變化敏感的區域，相當於不用考慮資料分佈變化了，這樣訓練起來更有效率。

那麼為什麼要有第4步，不是僅使用減均值除方差操作就能獲得目的效果嗎？我們思考一個問題，減均值除方差得到的分佈是正態分佈，我們能否認為正態分佈就是最好或最能體現我們訓練樣本的特徵分佈呢？不能，比如資料本身就很不對稱，或者啟用函式未必是對方差為1的資料最好的效果，比如Sigmoid啟用函式，在-1~1之間的梯度變化不大，那麼非線性變換的作用就不能很好的體現，換言之就是，減均值除方差操作後可能會削弱網路的效能！針對該情況，在前面三步之後加入第4步完成真正的batch normalization。

BN的本質就是利用優化變一下方差大小和均值位置，使得新的分佈更切合資料的真實分佈，保證模型的非線性表達能力。BN的極端的情況就是這兩個引數等於mini-batch的均值和方差，那麼經過batch normalization之後的資料和輸入完全一樣，當然一般的情況是不同的。

預測時均值和方差怎麼求？

在訓練時，我們會對同一批的資料的均值和方差進行求解，進而進行歸一化操作。但是對於預測時我們的均值和方差怎麼求呢？比如我們預測單個樣本時，那還怎麼求均值和方法呀！其實是這種樣子的，對於預測階段時所使用的均值和方差，其實也是來源於訓練集。比如我們在模型訓練時我們就記錄下每個batch下的均值和方差，待訓練完畢後，我們求整個訓練樣本的均值和方差期望值，作為我們進行預測時進行BN的的均值和方差：

最後測試階段，BN的使用公式就是：

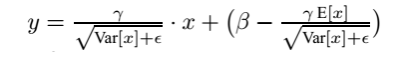
關於BN的使用位置，在CNN中一般應作用與非線性啟用函式之前，s型函式s(x)的自變數x是經過BN處理後的結果。因此前向傳導的計算公式就應該是：

其實因為偏置引數b經過BN層後其實是沒有用的，最後也會被均值歸一化，當然BN層後面還有個β引數作為偏置項，所以b這個引數就可以不用了。因此最後把BN層+啟用函式層就變成了：

CNN中的BN

注意前面寫的都是對於一般情況，對於卷積神經網路有些許不同。因為卷積神經網路的特徵是對應到一整張特徵響應圖上的，所以做BN時也應以響應圖為單位而不是按照各個維度。比如在某一層，batch大小為m，響應圖大小為w×h，則做BN的資料量為m×w×h。

BN在深層神經網路的作用非常明顯：若神經網路訓練時遇到收斂速度較慢，或者“梯度爆炸”等無法訓練的情況發生時都可以嘗試用BN來解決。同時，常規使用情況下同樣可以加入BN來加速模型訓練，甚至提升模型精度。

在機器學習中，我們非常關心模型的預測能力，即模型在新資料上的表現，而不希望過擬合現象的的發生，我們通常使用正則化（regularization）技術來防止過擬合情況。正則化是機器學習中通過顯式的控制模型複雜度來避免模型過擬合、確保泛化能力的一種有效方式。如果將模型原始的假設空間比作“天空”，那麼天空飛翔的“鳥”就是模型可能收斂到的一個個最優解。在施加了模型正則化後，就好比將原假設空間（“天空”）縮小到一定的空間範圍（“籠子”），這樣一來，可能得到的最優解能搜尋的假設空間也變得相對有限。有限空間自然對應複雜度不太高的模型，也自然對應了有限的模型表達能力。這就是“正則化有效防止模型過擬合的”一種直觀解析。

L2正則化

在深度學習中，用的比較多的正則化技術是L2正則化，其形式是在原先的損失函式後邊再加多一項：12λθ2i12λθi2，那加上L2正則項的損失函式就可以表示為：L(θ)=L(θ)+λ∑niθ2iL(θ)=L(θ)+λ∑inθi2，其中θθ就是網路層的待學習的引數，λλ則控制正則項的大小，較大的取值將較大程度約束模型複雜度，反之亦然。

L2約束通常對稀疏的有尖峰的權重向量施加大的懲罰，而偏好於均勻的引數。這樣的效果是鼓勵神經單元利用上層的所有輸入，而不是部分輸入。所以L2正則項加入之後，權重的絕對值大小就會整體傾向於減少，尤其不會出現特別大的值（比如噪聲），即網路偏向於學習比較小的權重。所以L2正則化在深度學習中還有個名字叫做“權重衰減”（weight decay），也有一種理解這種衰減是對權值的一種懲罰，所以有些書裡把L2正則化的這一項叫做懲罰項（penalty）。

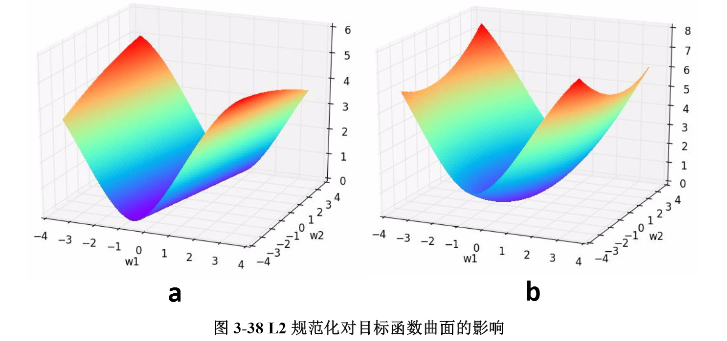
我們通過一個例子形象理解一下L2正則化的作用，考慮一個只有兩個引數w1w1和w2w2的模型，其損失函式曲面如下圖所示。從a可以看出，最小值所在是一條線，整個曲面看起來就像是一個山脊。那麼這樣的山脊曲面就會對應無數個引數組合，單純使用梯度下降法難以得到確定解。但是這樣的目標函式若加上一項0.1×(w21+w22)0.1×(w12+w22)，則曲面就會變成b圖的曲面，最小值所在的位置就會從一條山嶺變成一個山谷了,此時我們搜尋該目標函式的最小值就比先前容易了，所以L2正則化在機器學習中也叫做“嶺迴歸”（ridge regression）。

L1正則化

L1正則化的形式是：λ|θi|λ|θi|,與目標函式結合後的形式就是：L(θ)=L(θ)+λ∑ni|θi|L(θ)=L(θ)+λ∑in|θi|。需注意，L1 正則化除了和L2正則化一樣可以約束數量級外，L1正則化還能起到使引數更加稀疏的作用，稀疏化的結果使優化後的引數一部分為0，另一部分為非零實值。非零實值的那部分引數可起到選擇重要引數或特徵維度的作用，同時可起到去除噪聲的效果。此外，L1正則化和L2正則化可以聯合使用：λ1|θi|+12λ2θ2iλ1|θi|+12λ2θi2。這種形式也被稱為“Elastic網路正則化”。

正則化對偏導的影響

對於L2正則化：C=C0+λ2n∑iω2iC=C0+λ2n∑iωi2，相比於未加正則化之前,權重的偏導多了一項λnωλnω，偏置的偏導沒變化，那麼在梯度下降時ωω的更新變為：

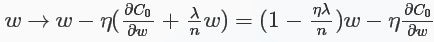
可以看出ωω的係數使得權重下降加速，因此L2正則也稱weight decay(caffe中損失層的weight_decay引數與此有關)。對於隨機梯度下降(對一個mini-batch中的所有x的偏導求平均)：

對於L1正則化：C=C0+λn∑i|ωi|C=C0+λn∑i|ωi|，梯度下降的更新為：

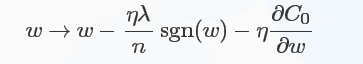
符號函式在ωω大於0時為1，小於0時為-1，在ω=0ω=0時|ω||ω|沒有導數，因此可令sgn(0)=0，在0處不使用L1正則化。
L1相比於L2，有所不同：

• L1減少的是一個常量，L2減少的是權重的固定比例
• 孰快孰慢取決於權重本身的大小，權重剛大時可能L2快，較小時L1快
• L1使權重稀疏，L2使權重平滑，一句話總結就是：L1會趨向於產生少量的特徵，而其他的特徵都是0，而L2會選擇更多的特徵，這些特徵都會接近於0

實踐中L2正則化通常優於L1正則化。