容斥原理及二維字首和
阿新 • • 發佈:2018-11-04
先mk一個容斥原理詳解
容斥原理大概就是 :
要計算幾個集合並集的大小,我們要先將所有單個集合的大小計算出來,然後減去所有兩個集合相交的部分,再加回所有三個集合相交的部分,再減去所有四個集合相交的部分,依此類推,一直計算到所有集合相交的部分。
引用葉學長的例子:
基本思想
A和B出現至少一人的概率(或方案數等)=A出現的概率+B出現的概率-兩人同時出現的概率。
更常見的應用:
A和B都不出現的概率=1-至少出現一人的概率,然後再容斥算後面那個東西。
更高階的應用:
n個A全部鴿鴿的概率=1-至少鴿一個的概率+至少鴿兩個的概率-......=1-至少鴿奇數個的概率+至少鴿偶數個的概率。
考試時如果感覺有點策不清就畫圖吧。。。韋恩圖是特別重要的解題手段
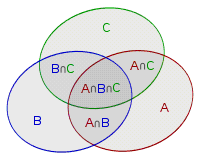
容斥原理基本公式
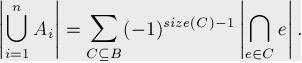
證明看容斥原理詳解
我們來看一道題
簡化後為:
硬幣購物一共有4種硬幣。面值分別為c1,c2,c3,c4。某人去商店買東西,去了tot次。每次帶di枚ci硬幣,買s的價值的東西。請問每次有多少種付款方法。
其中注意資料範圍di,s<=100000,tot<=1000。
本題如何用容斥原理:
引用題解的話:
簡單來說,就是把重複計算的部分去掉,把多去掉的部分加回來
針對本題而言,就是:
不合法數目=1超出的部分+2超出的部分+……1,2共同超出的部分-2,3共同超出的部分……+1,2,3共同超出的部分……(後面以此類推)
程式碼實現就比較容易了
貼上程式碼
#include<bits/stdc++.h>
using namespace std; #define int long long //這道題不開long long會爆int int t,k,n,m; int s; int ans=0; int f[100005],c[5],d[5];//f[i]為預處理的完全揹包 inline int read() //快讀 { char ch=getchar(); int x=0,q=1; while(ch>'9' || ch<'0')q=ch==45?-1:q,ch=getchar(); while(ch>='0' && ch<='9')x=(x<<1)+(x<<3)+(ch^'0'),ch=getchar(); return x*q; } inline void work() { f[0]=1; for(int i=1;i<=4;++i) for(int v=c[i];v<=100000;++v) f[v]+=f[v-c[i]]; } inline void dfs(int now,int s,int b) { if(s<0) return; if(now>4) { ans+=f[s]*b; return; }//剪枝 dfs(now+1,s,b);//求合法的部分 dfs(now+1,s-(d[now]+1)*c[now],-b);//求不合法的部分,b要變號所以乘以-1; } signed main() { for(int i=1;i<=4;++i) c[i]=read(); work(); t=read(); while(t) { --t; ans=0; for(int i=1;i<=4;i++) d[i]=read(); s=read(); dfs(1,s,1); printf("%lld\n",ans); } return 0; } 總結思路
先預處理f[i]表示在不限制硬幣數量的情況下購買價值為i的物品的方案數。於是我們可以跑一個完全揹包。
對於硬幣個數的限制,考慮容斥:欽定若干種硬幣使用di+1次,也就是欽定它超過限制。設被欽定的總費用為x,方案數就是f[s-x]。容斥一下,偶加奇減。
通過容斥原理,可以證明二維字首和的原理
具體證明為畫圖,直觀的表現出容斥原理的思想。
二維字首和,有效減少查詢統計時的複雜度,每一次查詢O(n)O(n)降到O(1),絕對過的了
記住:上加左,減左上,加自己
ans[i][j]=ans[i][j-1]+ans[i-1][j]-ans[i-1][j-1];
此題要用二維字首和優化
優化之後的程式碼
#include<bits/stdc++.h>
using namespace std; int t,k,n,m; long long c[2005][2005],ans[2005][2005];//ans表示二維字首和 inline void work() { c[0][0]=1; for(int i=1;i<=2000;++i) { c[i][0]=1; for(int j=1;j<=i;++j) { c[i][j]=(c[i-1][j]%k+c[i-1][j-1]%k)%k; ans[i][j]=ans[i-1][j]+ans[i][j-1]-ans[i-1][j-1];//二維字首和,上加左,減左上。 if(c[i][j]==0) ans[i][j]++;//加自己 } ans[i][i+1]=ans[i][i]; } } inline int read() { char ch=getchar(); int x=0,q=1; while(ch>'9' || ch<'0')q=ch==45?-1:q,ch=getchar(); while(ch>='0' && ch<='9')x=(x<<1)+(x<<3)+(ch^'0'),ch=getchar(); return x*q; } int main() { t=read(); k=read(); work(); while(t) { n=read(); m=read(); m=min(n,m); cout<<ans[n][m]<<endl; t--; } return 0; } 