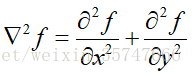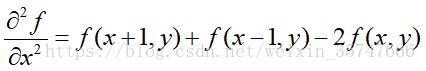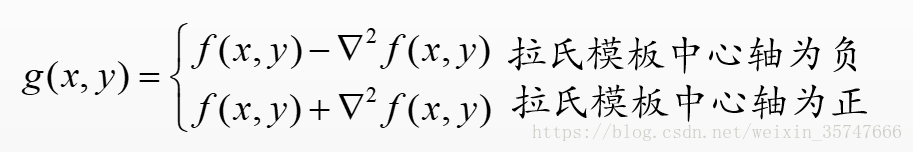上一節中我們講解了灰度變換的原理以及實現方法，本節我們講解空域濾波增強，與灰度變換相同，空域濾波增強是一種空域處理的方法，不過空域濾波不是一種對點做處理的方法，而是利用相鄰畫素間的關係進行增強。空域濾波可以按照增強效果的不同分為平滑與銳化兩類，又都可分為線性與非線性方法，線性濾波利用空域卷積來實現。接下來我們對平滑與銳化一一進行講解。

一、影象平滑

影象平滑的目的是抑制和消除噪聲，我們首先介紹一種線性平滑方法—鄰域平均，平滑運算元為

$A$

import cv2
import numpy as np 
import matplotlib.pyplot as plt 
import pylab

img = cv2.imread('Lena.jpg',1)
kernel = np.ones((5,5),np.float32)/25	#5×5卷積核，鄰域平均
res = cv2.filter2D(img,-1,kernel)
cv2.imshow('res',res)
cv2.waitKey(0)
 

opencv提供cv2.filter2D()函式來對影象進行卷積操作

dst = cv2.filter2D(src, ddepth, kernel[, dst[, anchor[, delta[, borderType]]]])
#dst：輸出影象
#src：輸入影象
#ddepth：輸出影象深度，-1為與原圖相同
#kernel：卷積核
#anchor：錨點，預設為(-1, -1)，指卷積核的中心點
#delta：輸出結果時的附加值，預設為0
#borderType：邊界模式，預設為BORDER_DEFAULT

我們採用不同大小的卷積核，依次對源影象進行卷積操作，結果如下，

卷積核半徑越大，影象平滑的效果越明顯，影象越來越模糊。
除了上述線性平滑方法之外，還有非線性平滑濾波器，包括中值濾波、百分比濾波、最大值濾波、最小值濾波，我們特別講解一下中值濾波，中值濾波是將選定的奇數畫素視窗內的各畫素灰度按大小排隊，用中間的灰度值代替視窗中原影象中間位置的畫素，因此是一種非線性濾波。中值濾波對既保留邊緣又要求去噪的任務很有用，尤其對椒鹽噪聲。
我們為Lena新增椒鹽噪聲，分別對其進行鄰域平均與中值濾波，實現程式碼如下，

import cv2
import numpy as np 
import matplotlib.pyplot as plt 
import random
import pylab

def cvToplt(img):	#經過顏色轉換後plt才能輸出彩色影象
	b,g,r = cv2.split(img)  
	img = cv2.merge([r,g,b])
	return img  
	
def main():	
	img = cv2.imread('Lena.jpg',1)
	x,y,z = img.shape
	for i in range(5000):	#新增椒鹽噪聲
		row = random.randint(0,x-1)
		col = random.randint(0,y-1)
		img[row][col] = 255
	kernel = np.ones((5,5),np.float32)/25
	res = cv2.filter2D(img,-1,kernel)	#鄰域平均
	res2=  cv2.medianBlur(img,5)	#中值濾波
	plt.subplot('131'),plt.imshow(cvToplt(img)),plt.title('Original')
	plt.subplot('132'),plt.imshow(cvToplt(res)),plt.title('mean')
	plt.subplot('133'),plt.imshow(cvToplt(res2)),plt.title('median')
	pylab.show()

if __name__ =="__main__":
	main()

結果如下，

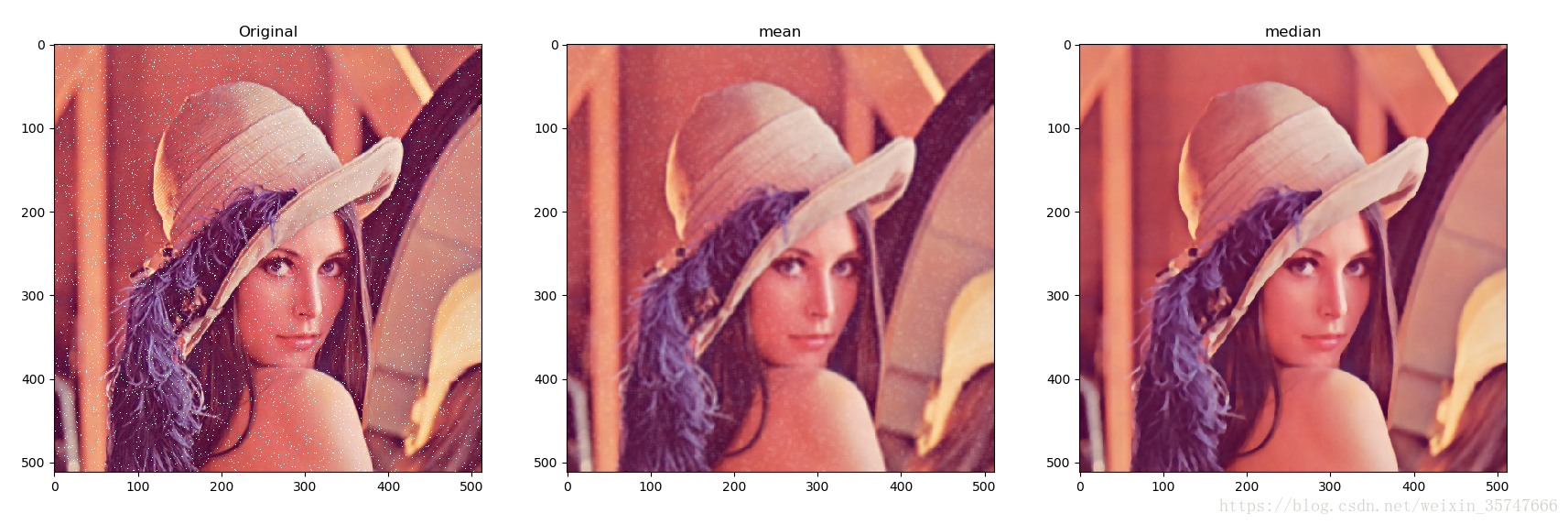
經過對比發現，中值濾波的去噪效果好，且能夠較好的保留影象邊緣，鄰域平均的平滑效果更好但去噪效果相對較差。

二、影象銳化

對正常的影象，通過銳化提取邊緣、輪廓、線條等資訊，供進一步識別。通過加重影象輪廓克服降質，以達到更好的視覺效果。常見的銳化演算法包括Roberts運算元、Sobel運算元、Prewitt運算元、拉普拉斯運算元。

（1）基於一階微分的影象增強—梯度法
我們把影象看成二維離散函式，為了提取影象的邊緣，我們需要計算影象的梯度，梯度是方向導數取最大值的方向的向量 ，影象的邊緣即為影象梯度較大的地方。
梯度用一個二維列向量來定義，

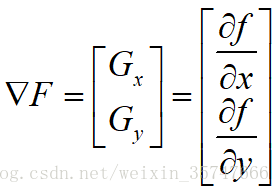
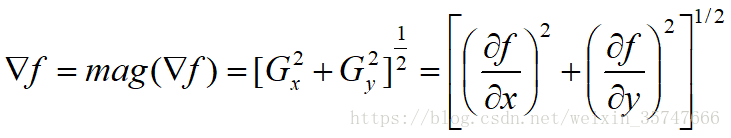
對於離散的二維影象，為計算方便，用絕對值代替幅值，用差分代替微分：
$（1）$
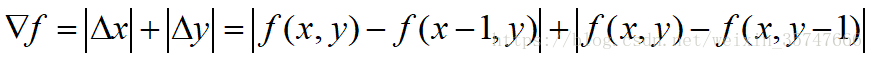
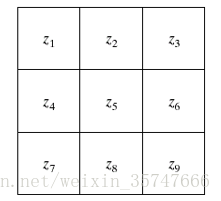
為了更好的理解，我們考慮一個3×3的影象區域，

$z$代表灰度級，由式 $（1）$，在點 $z_5$的 $▽f=|z_6-z_5|+|z_8-z_5|$

接下來我們來看Roberts交叉梯度， $z_5$的 $▽f=|z_9-z_5|+|z_8-z_6|$，我們發現計算方法發生了改變，可以理解為各種梯度運算元就是不同的梯度計算方法，由於上述的梯度公式本來就是近似的，因此沒有絕對的衡量方法，每種梯度運算元的功效各不相同，像第一種方式關注的是影象水平方向和垂直方向上的梯度，而Roberts交叉梯度則關注的是斜對角方向上的梯度。
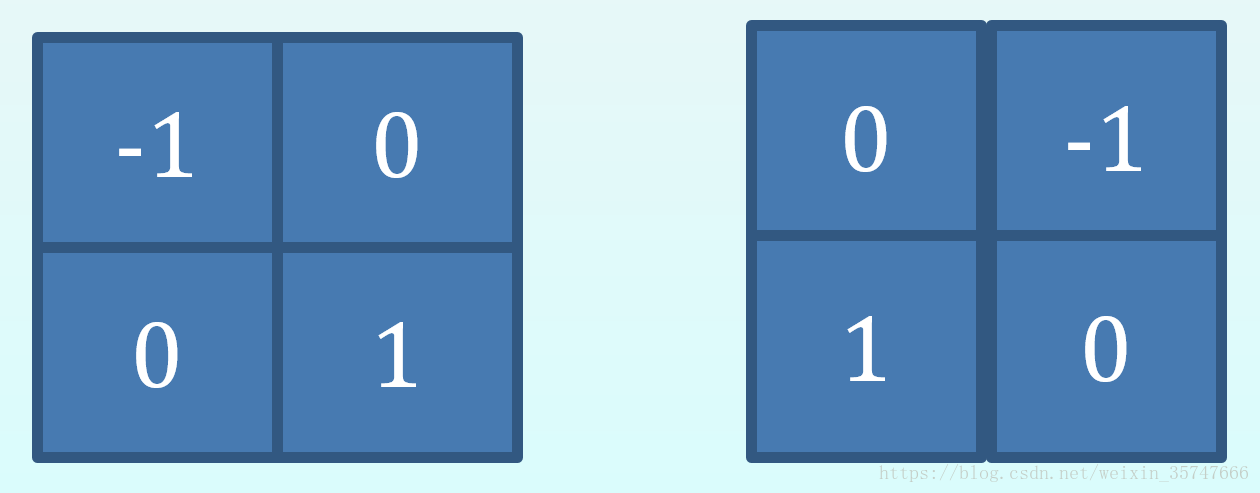
Roberts交叉梯度的計算由兩個模板組成，第一個模板求得梯度的第一項，第二個模板求得梯度的第二項，然後求和，得到梯度。兩個模板稱為Roberts交叉梯度運算元。

利用Roberts交叉梯度運算元對影象進行處理，實現程式碼如下，

import cv2
import numpy as np 
import matplotlib.pyplot as plt 
import pylab

def main():
	img = cv2.imread('Lena.jpg',0)
	plt.imshow(img,'gray')
	kernel_1 = np.array([[-1,0],[0,1]])  #Roberts運算元
	kernel_2 = np.array([[0,-1],[1,0]])
	res = cv2.filter2D(img,-1,kernel_1)
	res2 = cv2.filter2D(img,-1,kernel_2)
	plt.subplot(131),plt.imshow(res,'gray'),plt.title('1')
	plt.subplot(132),plt.imshow(res2,'gray'),plt.title('2')
	plt.subplot(133),plt.imshow(res+res2,'gray'),plt.title('1+2')
	pylab.show()

if __name__ == "__main__":
	main()

實驗結果如下，

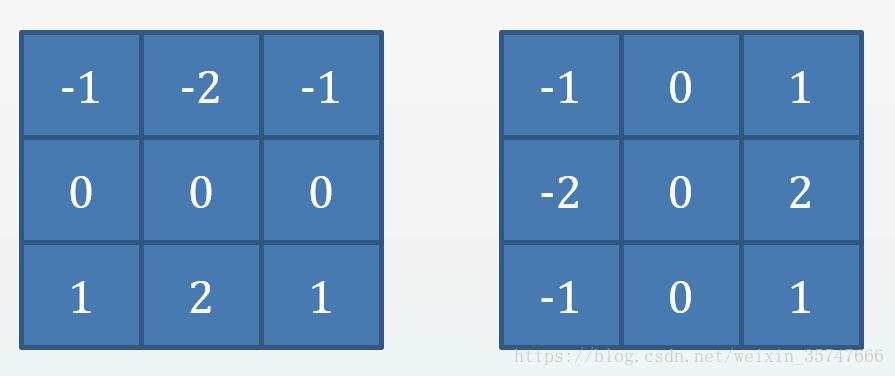
接下來我們學習Sobel梯度運算元，Sobel是一種3×3的梯度模板， $▽f=|(z_7+2z_8+z_9)-(z_1+2z_2+z_3)|+|(z_3+2z_6+z_9)-(z_1+2z_4+z_7)|$，

Sobel關注的是水平方向上與垂直方向上的梯度，這點與Roberts不同，Sobel實現程式碼如下，

import cv2
import numpy as np 
import matplotlib.pyplot as plt 
import pylab

def main():
	img = cv2.imread('Lena.jpg',0)
	kernel_1 = np.array([[-1,-2,-1],[0,0,0],[1,2,1]])	#Sobel運算元
	kernel_2 = np.array([[-1,0,1],[-2,0,2],[-1,0,1]])
	res = cv2.filter2D(img,-1,kernel_1)
	res2 = cv2.filter2D(img,-1,kernel_2)
	plt.subplot(131),plt.imshow(res,'gray'),plt.title('1')
	plt.subplot(132),plt.imshow(res2,'gray'),plt.title('2')
	plt.subplot(133),plt.imshow(res+res2,'gray'),plt.title('1+2')
	pylab.show()

if __name__ == "__main__":
	main()

實驗結果如下，

（2）基於二階微分的影象增強—拉普拉斯運算元
對影象求二階微分（近似），

在 $x$方向上，

在 $y$方向上，

則二階微分為
$▽^2f = [f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)]-4f(x,y)$
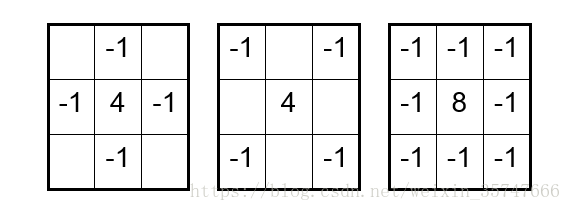
拉普拉斯運算元模板為

由於拉普拉斯是一種微分運算元，它的應用可增強影象中灰度突變的區域，減弱灰度的緩慢變化區域。
我們通常的做法是把原影象和拉普拉斯影象疊加在一起，這樣既能保護拉式銳化效果，同時又能復原背景資訊，具體的做法是：

當然，上述過程也可一步完成，更改拉普拉斯模板即可，如下（注意，此處模板中心只能為正，在以後的應用中，模板中心最好設為正值），

拉普拉斯運算元實現程式碼如下，

import cv2
import numpy as np 
import matplotlib.pyplot as plt 
import pylab

def main():
	img = cv2.imread('Lena.jpg',0)
	kernel = np.array([[0,-1,0],[-1,5,-1],[0,-1,0]])	#拉普拉斯運算元
	res = cv2.filter2D(img,-1,kernel)
	plt.subplot(121),plt.imshow(img,'gray'),plt.title('1')
	plt.subplot(122),plt.imshow(res,'gray'),plt.title('2')
	pylab.show()

if __name__ == "__main__":
	main()

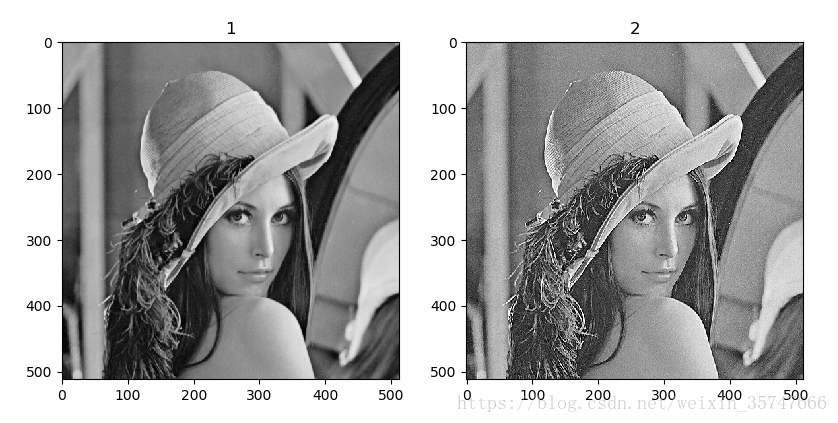
實驗結果如下，

總結一下，我們詳細講解了三種運算元，Roberts運算元、Sobel運算元和拉式運算元，前兩種屬於一階運算元，拉式運算元屬於二階運算元。通常我們在處理影象時，先會用拉式運算元突出影象中的小細節，後用梯度法突出影象的邊緣。

本節我們所講屬於影象增強技術中的空域濾波技術，即利用各種各樣的模板（運算元）對影象進行處理，後邊我們會講到基於頻域的影象處理技術。

未完待續