[HDU3544] Alice's Game(網上有些講解是錯的)
阿新 • • 發佈:2018-11-05
文章目錄
[HDU3544] Alice’s Game
題意:
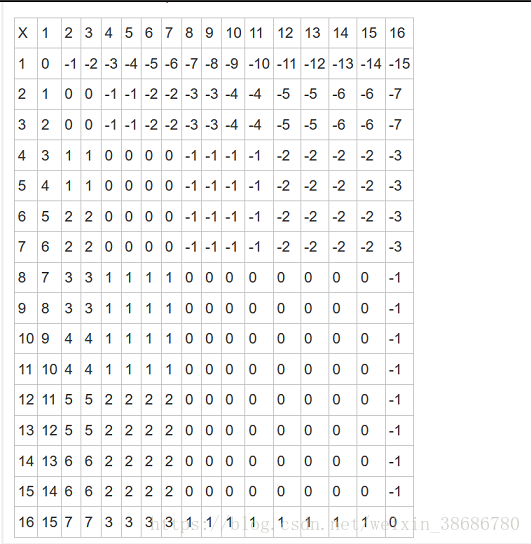
給n塊巧克力,第i塊是 ,Alice只能垂直切,切成 ,並且 ,Bob只能橫切,只能切成 ,並且
分析:
語言表達能力有限
我們採取
表示
的矩形對Alice的可切割次數的貢獻,負數代表對Bob的貢獻,如果所有
,Alice必贏,
,Bob(必贏)
對於HP(i,j) 的計算我們有如下法則
1.
的矩形貢獻為n-1
2.
的矩形貢獻為-(m-1)
3.
的矩形對HP的貢獻為零,因為如果你首先下手切,都會給對手更多的機會,如果你能贏,你不會切這個,如果你輸,那麼切了這個你還會輸。
4. 對於
的矩陣來說與3的狀況相同,對答案的貢獻都是0,首先下手都會給對手更多的機會
5. 貢獻為零的有什麼規律呢,我們發現原來是它們是
&&
6.
的矩形對於Alice來說有貢獻,我們每一次可以選擇都切成
的矩形,這樣不會給對手機會,自己還可以增加一次切的機會,Bob也不會傻到切這個矩形,這樣會給Alice更多機會,所以
的矩形,Alice 可以切
次
這個時候可以總結一下規律:
- 我們每一次切,都會切成 的 兩塊, ,遞迴下去 ,直到 ,這怎麼計算呢
- 我們知道 當且僅當 &&
- 那麼就有
參考程式碼
初級
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL solve(LL x,LL y)
{
LL t = 1;
while(t*2 <= y)
t <<= 1;
return x/t;
}
int main()
{
int T,n;
scanf("%d",&T);
for(int kase = 1; kase <= T; ++kase)
{
scanf("%d",&n);
LL x,y;
LL sum=0;
for(int i=1; i<=n; i++)
{
scanf("%lld%lld",&x,&y);
if(x > y) sum += solve(x,y)-1;
else sum -= solve(y,x) -1;
}
printf("Case %d: ",kase);
if(sum > 0) puts("Alice");
else puts("Bob");
}
return 0;
}
簡化
下面這個版本就是大家在其他部落格上看到的答案了
就是不停的對兩邊除以2,其實原理和
相同
#include <cstdio>
typedef long long LL;
int main()
{
int T; scanf("%d", &T);
for(int kase = 1; kase <= T; kase++)
{
int n; scanf("%d", &n);
LL a = 0, b = 0;
while(n--)
{
int x, y;
scanf("%d%d", &x, &y);
while(x > 1 && y > 1) { x >>= 1; y >>= 1; }
if(y == 1) a += (LL)x - 1;
if(x == 1) b += (LL)y - 1;
}
printf("Case %d: %s\n", kase, a > b ? "Alice" : "Bob");
}
return 0;
}