Net# 是由 Microsoft 開發的一種用於定義神經網路體系結構的語言。 使用 Net# 定義神經網路的結構使定義複雜結構（如深層神經網路或任意維度的卷積）變得可能，這些複雜結構被認為可提高對資料的學習，如映像、音訊或視訊。

在下列上下文中，可以使用 Net# 體系結構規範：

• Microsoft Azure 機器學習工作室中的所有網路模組：多類神經網路、兩類神經網路和神經網路迴歸
• MicrosoftML 中的神經網路函式：R 語言的 NeuralNet 和 rxNeuralNet，以及 Python 的 rx_neural_network
  。

本文介紹了使用 Net# 開發自定義神經網路的基本概念和所需語法：

• 神經網路要求以及如何定義主要元件
• Net# 規範語言的語法和關鍵字
• 使用 Net# 建立的自定義神經網路的示例

神經網路基礎知識

神經網路結構包括了在層中組織的節點，以及節點之間的加權連線（或邊緣）。 連線是有方向的，每個連線具有一個源節點和一個目標節點。

每個可訓練層（隱藏或輸出層）具有一個或多個連線捆綁。 連線捆綁包括一個源層和該源層中的連線規範。 給定捆綁中的所有連線共享同一源層和同一目標層。 在 Net # 中，連線捆綁將視為屬於捆綁的目標層。

Net # 支援各種型別的連線捆綁，可自定義對映到隱藏層和對映到輸出的輸入方式。

預設或標準捆綁是一個完整捆綁，其中源層中的每個節點都連線到目標層中的每個節點。

此外，Net# 支援以下四種高階連線捆綁：

• 篩選捆綁。 使用者可通過使用源層節點和目標層節點的位置來定義一個謂詞。 每當謂詞為 Ture，節點即連線。

• 卷積捆綁。 使用者可在源層中定義節點的小範圍鄰域。 目標層中的每個節點連線到源層中節點的一個鄰域。

• 池捆綁和響應規範化捆綁。 這些與卷積捆綁類似，使用者可在其中定義源層中小範圍的鄰域。 不同之處在於這些捆綁中邊緣的權重不可訓練。 相反，為源節點值應用預定義的函式可確定目標節點值。

支援的自定義項

在 Azure 機器學習中建立的神經網路模型的體系結構可通過使用 Net# 廣泛自定義。 可以：

• 建立隱藏層並控制每層的節點數。
• 指定如何相互連線層。
• 定義特殊的連線結構，如卷積和權重共享捆綁。
• 指定不同的啟用函式。

有關規範語言語法的詳細資訊，請參閱 結構規範。

有關為某些常見機器學習任務定義神經網路的示例（從單一到複雜），請參閱示例。

一般要求

• 必須正好是一個輸出層，至少一個輸入層，以及零個或多個隱藏層。
• 每層都有固定節點數，在任意維度的舉行陣列中按概念排列。
• 輸入層沒有關聯的訓練引數，並表示例項資料進入網路的點。
• 可訓練層（隱藏和輸出層）具有關聯的培訓引數，稱為權重和偏差。
• 源和目標節點必須處於不同的層。
• 連線必須是非迴圈的；換句話說，不能有導回初始源節點的連線鏈。
• 輸出層不能是連線捆綁的源層。

結構規範

神經網路結構規範由三部分組成：常數宣告、層宣告、連線宣告。 還有另一可選部分：共享宣告。 可以按任意順序指定這些部分。

常數宣告

常數宣告是可選的。 它提供了一種方法來定義神經網路定義中其他位置使用的值。 宣告語句包含識別符號（後跟一個等號和值表示式）。

例如，下面的語句定義一個常量 x：

Const X = 28;

要同時定義兩個或多個常量，可將識別符號名稱和值括在括號內，並使用分號隔開。 例如：

Const { X = 28; Y = 4; }

每個賦值表示式的右側可以是整數、實數、 布林值（True 或 False）或數學表示式。 例如：

Const { X = 17 * 2; Y = true; }

層宣告

層宣告是必需的。 它定義層的大小和源，包括其連線捆綁和屬性。 宣告語句以層（輸入、隱藏或輸出）名稱為開頭，後跟層的維度（正整數的元組）。 例如：

input Data auto;
hidden Hidden[5,20] from Data all;
output Result[2] from Hidden all; 

• 維度的乘積是層中節點數。 在此示例中，有兩個維度 [5,20]，這意味著層中有 100 個節點。
• 層可按任意順序進行宣告，但有一個例外：如果定義了多個輸入層，那麼宣告的順序必須與輸入資料中的功能順序匹配。

若要指定自動確定層中節點數，請使用 auto 關鍵字。 auto 關鍵字具有不同的效果，具體取決於層：

• 在輸入層宣告中，節點數是輸入資料中的功能數。
• 在隱藏層宣告中，節點數是隱藏節點數的引數值指定的數。
• 在輸出層宣告中，雙類分類的節點數是 2，迴歸的節點數是 1，最多分類的節點數與輸出節點數相等。

例如，以下網路定義可自動確定所有層的大小：

input Data auto;
hidden Hidden auto from Data all;
output Result auto from Hidden all;  

可訓練層（隱藏或輸出層）的層宣告可選擇包括輸出函式（也稱為啟用函式），這會分類模型預設為 sigmoid，迴歸模型預設為 linear。 即使使用預設值，為了清楚起見，也可以顯式宣告啟用函式。

支援以下輸出函式：

• sigmoid
• linear
• softmax
• rlinear
• square
• sqrt
• srlinear
• abs
• tanh
• brlinear

例如，下面的宣告使用 softmax 函式：

output Result [100] softmax from Hidden all;

連線宣告

定義可訓練層之後，必須宣告已定義的層中的連線。 連線捆綁以關鍵字 from 開頭，後跟捆綁的源層名稱以及要建立的連線捆綁的種類。

當前支援五種型別的連線捆綁：

• 完整捆綁，由關鍵字 all 指示
• 經篩選的捆綁，由後跟謂詞表達式的關鍵字 where 指示
• 卷積捆綁，由後跟卷積屬性的關鍵字 convolve 指示
• 池捆綁，由關鍵字 max pool 或 mean pool 指示
• 響應規範捆綁，由關鍵字 response norm 指示

完整捆綁

完整捆綁包括源層中每個節點到目標層中每個節點的連線。 這是預設網路連線型別。

篩選捆綁

篩選連線捆綁規範包含一個謂詞，在語法表達上，更類似 C# lambda 表示式。 下面的示例定義兩個篩選捆綁：

input Pixels [10, 20];
hidden ByRow[10, 12] from Pixels where (s,d) => s[0] == d[0];
hidden ByCol[5, 20] from Pixels where (s,d) => abs(s[1] - d[1]) <= 1; 

• 在 ByRow 的謂詞中，s 是輸入層 Pixels 的節點的矩形陣列中表示索引的引數，d 是隱藏層 ByRow 的節點的陣列中表示索引的引數。 s 和 d 的型別是長度為 2 的整數元組。 從概念上講，s 涵蓋了 0 <= s[0] < 10 且 0 <= s[1] < 20 的所有整數對，d 涵蓋了 0 <= d[0] < 10 且 0 <= d[1] < 12 的所有整數對。

• 在謂詞表達式的右側端上有一個條件。 在本例中，對於 s 和 d 的每個值，該條件為 True，從源層節點到目標層節點有一個邊緣。 因此，在所有 s[0] 等於 d[0] 的情況下，此篩選表示式指示捆綁包括從由 s 定義的節點到由 d 定義的節點的連線。

或者，可以為篩選的捆綁指定一組權重。 Weights 屬性的值必須是浮點值的元組，其長度與捆繫結義的連線數匹配。 預設情況下，權重是隨機生成的。

權重值按照目標節點索引進行分組。 也就是說，在源索引順序中，如果第一個目標節點連線到 K 源節點，則 Weights 元組的前 K 個元素為第一個目標節點的權重。 這同樣適用於其他目標節點。

可直接將權重指定為常量值。 例如，如果以前瞭解權重，則可以使用此語法將其指定為常量：

const Weights_1 = [0.0188045055, 0.130500451, ...]

卷積捆綁

如果訓練資料具有同類結構，則通常使用卷積捆綁來了解資料的高階功能。 例如，映像、音訊或視訊資料中的空間或臨時維數可以很統一。

卷積捆綁使用通過維度滑動的矩形核心。 實質上，每個核心定義一組在本地鄰域中應用的權重，稱為核心應用程式。 每個核心應用程式對應一個源層中的節點，稱為核心節點。 核心的權重在多個連線中共享。 在卷積捆綁中，每個核心都是矩形狀的，並且所有核心應用程式都具有相同大小。

卷積捆綁支援一下屬性：

InputShape 可定義用於此卷積捆綁的源層維數。 值必須是正整數的元組。 整數的乘積必須等於源層中的節點數，否則，不需要與源層宣告的維數匹配。 此元組的長度會成為卷積捆綁的實引數量值。 通常，實引數量表示函式可採用的引數或操作的數量。

若要定義核心的形狀和位置，可使用屬性 KernelShape、Stride、Padding、LowerPad 或 UpperPad：

• KernelShape：（必需）為卷積捆繫結義每個核心的維數。 值必須是正整數的元組，其長度等於捆綁的實引數量。 此元組的每個元件必須不超過 InputShape 的相應元件。

• Stride：（可選）定義卷積的滑動步大小（每個維度的每步大小），即中央節點之間的距離。 值必須是正整數的元組，其長度為捆綁的實引數量。 此元組的每個元件必須不超過 KernelShape 的相應元件。 預設值為一個元組，其所有元件都等於 1。

• Sharing：（可選）定義卷積的每個維度的權重共享。 值可以是單個布林值或布林值的元組（其長度為捆綁的實引數量）。 單個布林值擴充套件為正確長度的元組，所有元件都等於指定值。 預設值為包含所有 True 值的元組。

• MapCount：（可選）為卷積捆繫結義功能對映數。 值可以是單個正整數或正整數的元組（其長度為捆綁的實引數量）。 單個整數值擴充套件為正確長度的元組，第一個元件等於指定值，其他所有元件等於 1. 預設值為 1。 功能對映的總數是元組元件的乘積。元件之間的總數的因數分解可確定目標節點中功能對映值的分組方式。

• Weights：（可選）定義捆綁的初始權重。 值必須是浮點值的元組，其長度為核心數乘以每個核心的權重數，會在本文後面部分中定義。 預設權重是隨機生成的。

有兩組控制填充的屬性，這兩個屬性相互排斥：

• Padding：（可選）確定是否應該使用預設填充方案來填充輸入。 值可以是單個布林值或布林值的元組（其長度為捆綁的實引數量）。

  單個布林值擴充套件為正確長度的元組，所有元件都等於指定值。

  如果維度值為 True，則使用零值單元格將源按邏輯填充到維度以支援其他核心應用程式，從而使該維度中第一個和最後一個核心的中央節點稱為源層的維度中的第一個和最後一個節點。 因此，每個維度中的“虛擬”節點數將自動確定，以使 (InputShape[d] - 1) / Stride[d] + 1 核心完全符合填充的源層。

  如果維度值為 False，則將定義核心，使留出的每個端上的節點數都相同（最大差值為 1）。 此屬性的預設值為一個元組，其所有元件都等於 False。

• UpperPad 和 LowerPad：（可選）對大量要使用的填充提供更好的控制。 重要提示： 當且僅當沒有定義上述的 Padding 屬性時，才能定義這些屬性。 值必須是正整數值的元組，其長度為繫結的實引數量。 指定這些屬性後，“虛擬”節點將新增到輸入層的每個維度的上下兩端。 每個維度的上下兩端新增的節點數分別由 LowerPad[i] 和 UpperPad[i] 確定。

  若要確保核心只對應“真實”節點而不是“虛擬”節點，則必須符合以下條件：

  • LowerPad 的每個元件必須嚴格小於 KernelShape[d]/2。
  • UpperPad 的每個元件不能大於 KernelShape[d]/2。

  • 這些屬性的預設值為一個元組，其所有元件都等於 0。

    設定 Padding = true 允許儘可能多的填充，使核心的“中心”保持在“真實”輸入內。 這會對數學做出一些更改，以便計算輸出大小。 通常情況下，輸出大小 D 計算為 D = (I - K) / S + 1，其中 I 是輸入大小，K 是核心大小，S 是 stride，/ 表示整數除法（向零舍入）。 如果設定 UpperPad = [1, 1]，則輸入大小 I 實際上是 29，因此 D = (29 - 5) / 2 + 1 = 13。 但是，當 Padding = true 時，I 實際上增長 K - 1，因此 D = ((28 + 4) - 5) / 2 + 1 = 27 / 2 + 1 = 13 + 1 = 14。 通過為 UpperPad 和 LowerPad 指定值，相比只設置 Padding = true，可以更好地控制填充。

有關卷積網路及其應用程式的詳細資訊，請參閱這些文章：

• http://deeplearning.net/tutorial/lenet.html
• http://research.microsoft.com/pubs/68920/icdar03.pdf
• http://people.csail.mit.edu/jvb/papers/cnn_tutorial.pdf

池捆綁

池捆綁適用於類似卷積連線的幾何，但是它使用源節點的預定義函式來派生目標節點值。 因此，池捆綁不具有可訓練狀態（權重或偏差）。 池捆綁支援所有卷積屬性，除了 Sharing、MapCount 和 Weights。

通常情況下，按相鄰池單位彙總的核心不會重疊。 如果在每個維度中 Stride[d] 等於KernelShape[d] ，那麼獲取的層為傳統本地池層，其廣泛應用於卷積神經網路。 每個目標節點將計算源層中其核心的最大活動數或平均值。

以下示例對池捆綁進行了說明：

hidden P1 [5, 12, 12]
  from C1 max pool {
  InputShape  = [ 5, 24, 24];
   KernelShape = [ 1,  2,  2];
   Stride      = [ 1,  2,  2];
  }  

• 捆綁的實引數量為 3，也就是元組 InputShape、KernelShape 和 Stride 的長度。
• 源層中的節點數為 5 * 24 * 24 = 2880。
• 這是傳統本地池層，因為 KernelShape 和 Stride 相等。
• 目標層中的節點數為 5 * 12 * 12 = 1440。

有關池層的詳細資訊，請參閱這些文章：

• http://www.cs.toronto.edu/~hinton/absps/imagenet.pdf（第 3.4 節）
• http://cs.nyu.edu/~koray/publis/lecun-iscas-10.pdf
• http://cs.nyu.edu/~koray/publis/jarrett-iccv-09.pdf

響應規範化捆綁

響應規範化是本地規範化方案，由 Geoffrey Hinton 等人在文章 ImageNet Classification with Deep Convolutional Neural Networks（深層卷積神經網路的 ImageNet 分類）中首次引入。

響應規範化用於避免神經網路中的通用化。 一個神經元在一個非常高的啟用級別中激發時，本地響應規範化層將抑制周圍神經元的啟用級別。 這是通過使用三個引數（α、β 和 k）和一個卷積結構（或鄰域形狀）來完成的。 目標層 y 中的每個神經元對應於源層中神經元 x。 y 的啟用級別由以下公式指定，其中 f 是神經元的啟用級別，Nx 是核心（或包含 x 鄰域中神經元的集），由以下卷積結構定義：

 

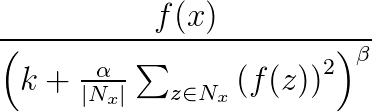
響應規範化捆綁支援所有卷積屬性，除了 Sharing、MapCount 和 Weights。

• 如果核心包含與 x 相同的對映中的神經元，則規範化方案稱為相同對映規範化。 若要定義相同對映規範化，那麼 InputShape 中的第一個座標必須具有值 1.

• 如果核心包含與 x 相同的空間位置中的神經元，但是神經元位於其他對映中，則規範化方案稱為跨對映規範化。 這種型別的響應規範化可實現一種橫向抑制，其靈感來源於從真實神經元中發現的型別，可建立不同對映上計算的神經元輸出之間的大啟用級別的競爭。 若要定義跨對映規範化，第一個座標必須是大於 1 且不大於對映數的正整數，其他座標則必須具有值 1.

因為響應規範化捆綁應用源節點值的預定義函式以確定目標節點值，所以它們不具有可訓練狀態（權重或偏差）。

 備註

目標層中的節點對應於是核心的中央節點的神經元。 例如，如果 KernelShape[d] 為奇數，則 KernelShape[d]/2 對應於中央核心節點。 如果 KernelShape[d] 為偶數，則中央節點位於 KernelShape[d]/2 - 1。 因此，如果 Padding[d] 為 False，則第一個和最後一個 KernelShape[d]/2 節點在目標層中沒有對應節點。 要避免這種情況，可將 Padding 定義為 [true, true, …, true]。

除了前面所述的四個屬性，響應規範化捆綁還支援以下屬性：

• Alpha：（必需）指定一個與前面公式中的 α 對應的浮點值。
• Beta：（必需）指定一個與前面公式中的 β 對應的浮點值。
• Offset：（可選）指定一個與前面公式中的 k 對應的浮點值。 預設為 1。

下面的示例使用這些屬性定義迴應規範化捆綁：

hidden RN1 [5, 10, 10]
from P1 response norm {
  InputShape  = [ 5, 12, 12];
  KernelShape = [ 1,  3,  3];
  Alpha = 0.001;
  Beta = 0.75;
  } 

• 源層包括五個對映，每個具有一個 12x12 維度，總計 1440 個節點。
• 值 KernelShape 指示這是一個相同的對映規範化層，其中鄰域為一個 3x3 矩形。
• Padding 的預設值為 False，因此目標層的每個維度中只有 10 個節點。 要包括一個與源層中每個節點對應的目標層中的節點，可新增 Padding = [true, true, true]；然後將 RN1 的大小更改為 [5, 12, 12]。

共享宣告

Net # 可選擇支援定義具有共享權重的多個捆綁。 如果任意兩個捆綁的結構相同，則其權重可以共享。 以下語法可定義具有共享權重的捆綁：

share-declaration:
  share    {    layer-list    }
  share    {    bundle-list    }
  share    {    bias-list    }

  layer-list:
    layer-name    ,    layer-name
    layer-list    ,    layer-name

  bundle-list:
    bundle-spec    ,    bundle-spec
    bundle-list    ,    bundle-spec

  bundle-spec:
    layer-name    =>     layer-name

  bias-list:
    bias-spec    ,    bias-spec
    bias-list    ,    bias-spec

  bias-spec:
    1    =>    layer-name

  layer-name:
    identifier

例如，以下共享宣告指定層名稱，指示應共享兩個權重和偏差：

Const {
  InputSize = 37;
  HiddenSize = 50;
  }
input {
  Data1 [InputSize];
  Data2 [InputSize];
  }
hidden {
  H1 [HiddenSize] from Data1 all;
  H2 [HiddenSize] from Data2 all;
  }
output Result [2] {
  from H1 all;
  from H2 all;
  }
share { H1, H2 } // share both weights and biases  

• 輸入功能劃分為兩個相等大小的輸入層。
• 隱藏層則計算兩個輸入層上的更高級別的功能。
• 共享宣告指定 H1 和 H2 必須從其各自的輸入中以相同的方式進行計算。

或者，可以使用兩個單獨的共享宣告來指定，如下所示：

share { Data1 => H1, Data2 => H2 } // share weights  
<!-- -->
share { 1 => H1, 1 => H2 } // share biases  

只有在層包含單個捆綁時，才可以使用縮寫形式。 一般情況下，只有在相關結構相同時（即具有相同大小、相同卷積幾何等），才能共享。

Net # 用法的示例

本部分提供了一些示例，可瞭解如何使用 Net# 新增隱藏層，定義隱藏層與其它層互動的方式，以及生成卷積網路。

定義一個簡單的自定義神經網路：“Hello World”示例

這個簡單的示例演示瞭如何建立具有單個隱藏層的神經網路模型。

input Data auto;
hidden H [200] from Data all;
output Out [10] sigmoid from H all;  

該示例闡釋了一些基本的命令，如下所示：

• 第一行定義了輸入層（名為 Data）。 使用 auto 關鍵字時，神經網路會自動包括輸入示例中的所有功能列。
• 第二行建立隱藏層。 為該隱藏層指定了名稱 H，該層有 200 個節點。 這一層完全連線到輸入層。
• 第三行定義了輸出層（名為 O），其中包含 10 個輸出節點。 如果神經網路用於分類，則每個類有一個輸出節點。 關鍵字 sigmoid 指示輸出函式將應用於輸出層。

定義多個隱藏層：計算機影像示例

下面的示例將演示如何使用多個自定義隱藏層，定義稍微複雜一些的神經網路。

// Define the input layers 
input Pixels [10, 20];
input MetaData [7];

// Define the first two hidden layers, using data only from the Pixels input
hidden ByRow [10, 12] from Pixels where (s,d) => s[0] == d[0];
hidden ByCol [5, 20] from Pixels where (s,d) => abs(s[1] - d[1]) <= 1;

// Define the third hidden layer, which uses as source the hidden layers ByRow and ByCol
hidden Gather [100] 
{
from ByRow all;
from ByCol all;
}

// Define the output layer and its sources
output Result [10]  
{
from Gather all;
from MetaData all;
}  

此示例說明了神經網路規範語言的多個功能：

• 此結構中包含兩個輸入層：Pixels 和 MetaData。
• Pixels 層是兩個連線捆綁的源層（目標層為 ByRow 和 ByCol）。
• 層 Gather 和 Result 是多個連線捆綁中的目標層。
• 輸出層 Result 是兩個連線捆綁中的目標層；一個以第二級隱藏層 Gather 作為目標層，另一個以輸入層 MetaData 作為目標層。
• 隱藏層 ByRow 和 ByCol 使用謂詞表達式指定經篩選的連線。 更確切地說，ByRow 中 [x, y] 處的節點連線到 Pixels 中第一個索引座標等於節點的第一個座標 x 的節點。 同樣，ByCol 中 [x, y] 處的節點連線到 Pixels 中第二個索引座標位於節點的第二個座標 y 內的節點。

為多類分類定義卷積網路：數字識別示例

以下網路的定義旨在識別數字，並說明了自定義神經網路的一些高階技術。

input Image [29, 29];
hidden Conv1 [5, 13, 13] from Image convolve 
  {
  InputShape  = [29, 29];
  KernelShape = [ 5,  5];
  Stride      = [ 2,  2];
  MapCount    = 5;
  }
hidden Conv2 [50, 5, 5]
from Conv1 convolve 
  {
  InputShape  = [ 5, 13, 13];
  KernelShape = [ 1,  5,  5];
  Stride      = [ 1,  2,  2];
  Sharing     = [false, true, true];
  MapCount    = 10;
  }
hidden Hid3 [100] from Conv2 all;
output Digit [10] from Hid3 all;  

• 此結構具有單個輸入層 Image。
• 關鍵字 convolve 指示名為 Conv1 和 Conv2 的層是卷積層。 每個這些層宣告都後跟一個卷積屬性列表。
• Net 具有第三個隱藏層 Hid3，該層完全連線到第二個隱藏層 Conv2。
• 輸出層 Digit 僅連線到第三個隱藏層 Hid3。 關鍵字 all 指示輸出層完全連線到 Hid3。
• 卷積的實引數量為 3：元組 InputShape、KernelShape、Stride, and 的長度。
• 每個核心的權重數為 1 + KernelShape\[0] * KernelShape\[1] * KernelShape\[2] = 1 + 1 * 5 * 5 = 26 或 26 * 50 = 1300。

• 可以計算每個隱藏層中的節點，如下所示：

  NodeCount\[0] = (5 - 1) / 1 + 1 = 5 NodeCount\[1] = (13 - 5) / 2 + 1 = 5 NodeCount\[2] = (13 - 5) / 2 + 1 = 5

• 可通過使用層的宣告維數 [50, 5, 5] 來計算節點總數，如下所示：MapCount * NodeCount\[0] * NodeCount\[1] * NodeCount\[2] = 10 * 5 * 5 * 5

• 因為只有 d == 0 時 Sharing[d] 為 False，因此核心數為 MapCount * NodeCount\[0] = 10 * 5 = 50。

 

用於自定義神經網路體系結構的 Net# 語言由 Microsoft 的 Shon Katzenberger（架構師，機器學習）和 Alexey Kamenev（軟體工程師，Microsoft Research）開發。 在內部，其用於機器學習專案和應用程式，其範圍包括從映像檢測到文字分析。 有關詳細資訊，請參閱 Neural Nets in Azure ML - Introduction to Net#（Azure ML 中的神經網路 - Net# 簡介）