轉自：http://www.ruanyifeng.com/blog/2017/07/neural-network.html

眼下最熱門的技術，絕對是人工智慧。

人工智慧的底層模型是"神經網路"（neural network）。許多複雜的應用（比如模式識別、自動控制）和高階模型（比如深度學習）都基於它。學習人工智慧，一定是從它開始。

什麼是神經網路呢？網上似乎缺乏通俗的解釋。

前兩天，我讀到 Michael Nielsen 的開源教材《神經網路與深度學習》（Neural Networks and Deep Learning），意外發現裡面的解釋非常好懂。下面，我就按照這本書，介紹什麼是神經網路。

這裡我要感謝優達學城的贊助，本文結尾有他們的《前端開發（進階）》課程的訊息，歡迎關注。

一、感知器

歷史上，科學家一直希望模擬人的大腦，造出可以思考的機器。人為什麼能夠思考？科學家發現，原因在於人體的神經網路。

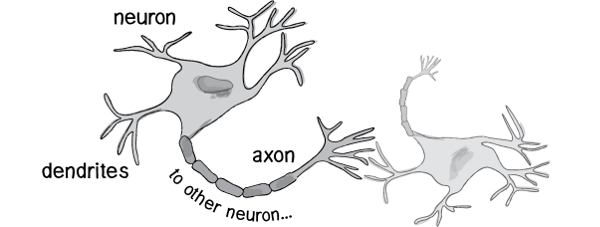
1. 外部刺激通過神經末梢，轉化為電訊號，轉導到神經細胞（又叫神經元）。
2. 無數神經元構成神經中樞。
3. 神經中樞綜合各種訊號，做出判斷。
4. 人體根據神經中樞的指令，對外部刺激做出反應。

既然思考的基礎是神經元，如果能夠"人造神經元"（artificial neuron），就能組成人工神經網路，模擬思考。上個世紀六十年代，提出了最早的"人造神經元"模型，叫做

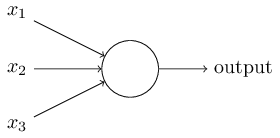
上圖的圓圈就代表一個感知器。它接受多個輸入（x1，x2，x3...），產生一個輸出（output），好比神經末梢感受各種外部環境的變化，最後產生電訊號。

為了簡化模型，我們約定每種輸入只有兩種可能：1 或 0。如果所有輸入都是1，表示各種條件都成立，輸出就是1；如果所有輸入都是0，表示條件都不成立，輸出就是0。

二、感知器的例子

下面來看一個例子。城裡正在舉辦一年一度的遊戲動漫展覽，小明拿不定主意，週末要不要去參觀。

他決定考慮三個因素。

1. 天氣：週末是否晴天？
2. 同伴：能否找到人一起去？
3. 價格：門票是否可承受？

這就構成一個感知器。上面三個因素就是外部輸入，最後的決定就是感知器的輸出。如果三個因素都是 Yes（使用1表示），輸出就是1（去參觀）；如果都是 No（使用0表示），輸出就是0（不去參觀）。

三、權重和閾值

看到這裡，你肯定會問：如果某些因素成立，另一些因素不成立，輸出是什麼？比如，週末是好天氣，門票也不貴，但是小明找不到同伴，他還要不要去參觀呢？

現實中，各種因素很少具有同等重要性：某些因素是決定性因素，另一些因素是次要因素。因此，可以給這些因素指定權重（weight），代表它們不同的重要性。

• 天氣：權重為8
• 同伴：權重為4
• 價格：權重為4

上面的權重表示，天氣是決定性因素，同伴和價格都是次要因素。

如果三個因素都為1，它們乘以權重的總和就是 8 + 4 + 4 = 16。如果天氣和價格因素為1，同伴因素為0，總和就變為 8 + 0 + 4 = 12。

這時，還需要指定一個閾值（threshold）。如果總和大於閾值，感知器輸出1，否則輸出0。假定閾值為8，那麼 12 > 8，小明決定去參觀。閾值的高低代表了意願的強烈，閾值越低就表示越想去，越高就越不想去。

上面的決策過程，使用數學表達如下。

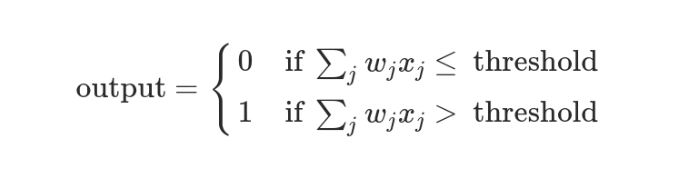
上面公式中，x表示各種外部因素，w表示對應的權重。

四、決策模型

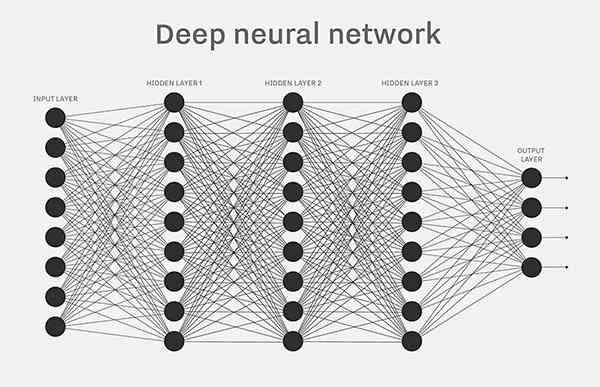
單個的感知器構成了一個簡單的決策模型，已經可以拿來用了。真實世界中，實際的決策模型則要複雜得多，是由多個感知器組成的多層網路。

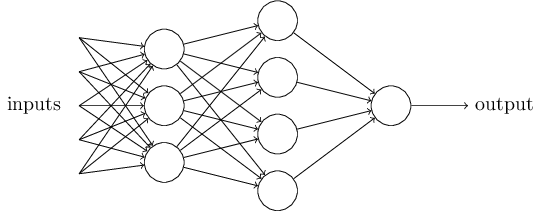
上圖中，底層感知器接收外部輸入，做出判斷以後，再發出訊號，作為上層感知器的輸入，直至得到最後的結果。（注意：感知器的輸出依然只有一個，但是可以傳送給多個目標。）

這張圖裡，訊號都是單向的，即下層感知器的輸出總是上層感知器的輸入。現實中，有可能發生迴圈傳遞，即 A 傳給 B，B 傳給 C，C 又傳給 A，這稱為"遞迴神經網路"（recurrent neural network），本文不涉及。

五、向量化

為了方便後面的討論，需要對上面的模型進行一些數學處理。

• 外部因素 x1、x2、x3 寫成向量 <x1, x2, x3>，簡寫為 x
• 權重 w1、w2、w3 也寫成向量 (w1, w2, w3)，簡寫為 w
• 定義運算 w⋅x = ∑ wx，即 w 和 x 的點運算，等於因素與權重的乘積之和
• 定義 b 等於負的閾值 b = -threshold

感知器模型就變成了下面這樣。

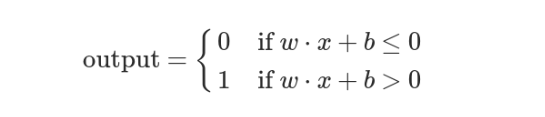
六、神經網路的運作過程

一個神經網路的搭建，需要滿足三個條件。

• 輸入和輸出
• 權重（w）和閾值（b）
• 多層感知器的結構

也就是說，需要事先畫出上面出現的那張圖。

其中，最困難的部分就是確定權重（w）和閾值（b）。目前為止，這兩個值都是主觀給出的，但現實中很難估計它們的值，必需有一種方法，可以找出答案。

這種方法就是試錯法。其他引數都不變，w（或b）的微小變動，記作Δw（或Δb），然後觀察輸出有什麼變化。不斷重複這個過程，直至得到對應最精確輸出的那組w和b，就是我們要的值。這個過程稱為模型的訓練。

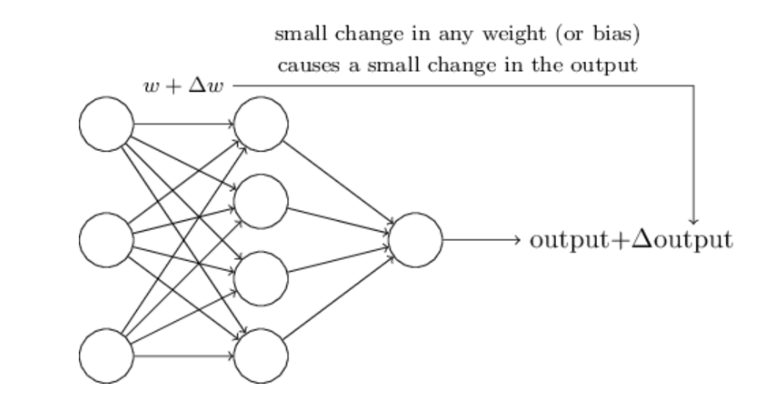
因此，神經網路的運作過程如下。

1. 確定輸入和輸出
2. 找到一種或多種演算法，可以從輸入得到輸出
3. 找到一組已知答案的資料集，用來訓練模型，估算w和b
4. 一旦新的資料產生，輸入模型，就可以得到結果，同時對w和b進行校正

可以看到，整個過程需要海量計算。所以，神經網路直到最近這幾年才有實用價值，而且一般的 CPU 還不行，要使用專門為機器學習定製的 GPU 來計算。

七、神經網路的例子

下面通過車牌自動識別的例子，來解釋神經網路。

所謂"車牌自動識別"，就是高速公路的探頭拍下車牌照片，計算機識別出照片裡的數字。

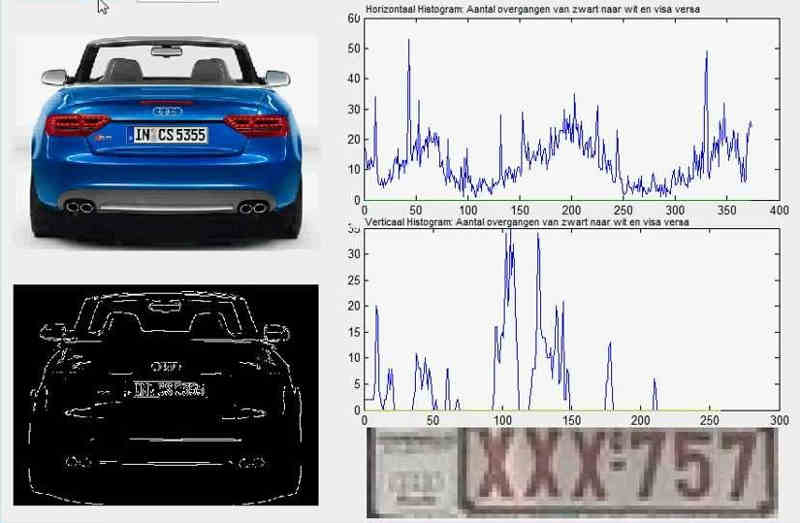
這個例子裡面，車牌照片就是輸入，車牌號碼就是輸出，照片的清晰度可以設定權重（w）。然後，找到一種或多種影象比對演算法，作為感知器。演算法的得到結果是一個概率，比如75%的概率可以確定是數字1。這就需要設定一個閾值（b）（比如85%的可信度），低於這個門檻結果就無效。

一組已經識別好的車牌照片，作為訓練集資料，輸入模型。不斷調整各種引數，直至找到正確率最高的引數組合。以後拿到新照片，就可以直接給出結果了。

八、輸出的連續性

上面的模型有一個問題沒有解決，按照假設，輸出只有兩種結果：0和1。但是，模型要求w或b的微小變化，會引發輸出的變化。如果只輸出0和1，未免也太不敏感了，無法保證訓練的正確性，因此必須將"輸出"改造成一個連續性函式。

這就需要進行一點簡單的數學改造。

首先，將感知器的計算結果wx + b記為z。

z = wx + b

然後，計算下面的式子，將結果記為σ(z)。

σ(z) = 1 / (1 + e^(-z)) 

這是因為如果z趨向正無窮z → +∞（表示感知器強烈匹配），那麼σ(z) → 1；如果z趨向負無窮z → -∞（表示感知器強烈不匹配），那麼σ(z) → 0。也就是說，只要使用σ(z)當作輸出結果，那麼輸出就會變成一個連續性函式。

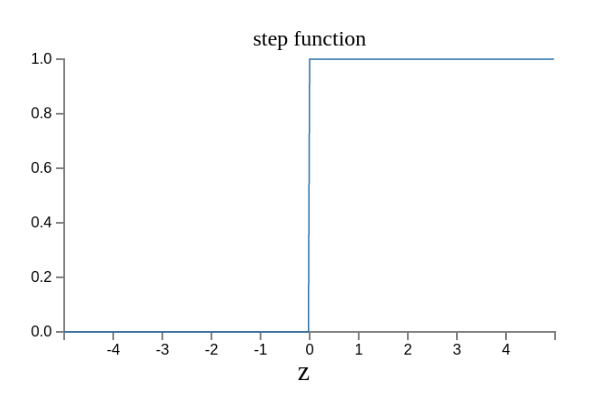
原來的輸出曲線是下面這樣。

現在變成了這樣。

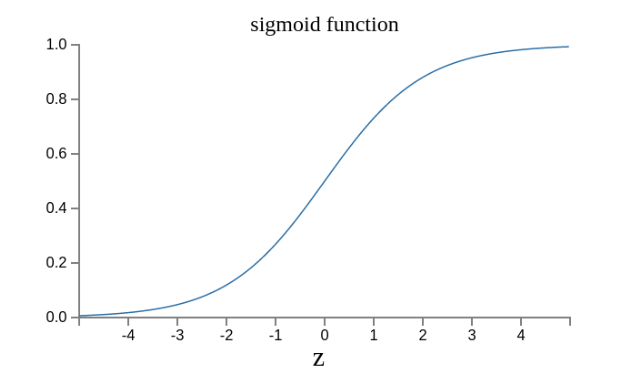
實際上，還可以證明Δσ滿足下面的公式。

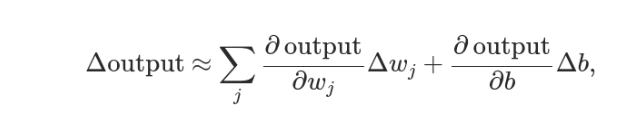
即Δσ和Δw和Δb之間是線性關係，變化率是偏導數。這就有利於精確推算出w和b的值了。