農民John的農場裡有很多牧區。有的路徑連線一些特定的牧區。一片所有連通的牧區稱為一個牧場。但是就目前而言，你能看到至少有兩個牧區不連通。現在，John想在農場裡新增一條路徑 ( 注意，恰好一條 )。對這條路徑有這樣的限制：一個牧場的直徑就是牧場中最遠的兩個牧區的距離 ( 本題中所提到的所有距離指的都是最短的距離 )。考慮如下的兩個牧場，圖１是有5個牧區的牧場，牧區用“*”表示，路徑用直線表示。每一個牧區都有自己的座標：

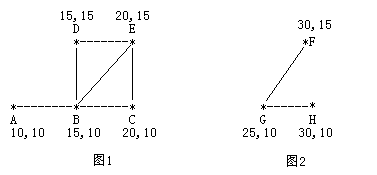
圖１所示的牧場的直徑大約是12.07106, 最遠的兩個牧區是A和E，它們之間的最短路徑是A-B-E。

這兩個牧場都在John的農場上。John將會在兩個牧場中各選一個牧區，然後用一條路徑連起來，使得連通後這個新的更大的牧場有最小的直徑。注意，如果兩條路徑中途相交，我們不認為它們是連通的。只有兩條路徑在同一個牧區相交，我們才認為它們是連通的。

現在請你程式設計找出一條連線兩個不同牧場的路徑，使得連上這條路徑後，這個更大的新牧場有最小的直徑。

輸入

第 1 行：一個整數N (1 ≤ N ≤ 150), 表示牧區數；

第 2 到 N+1 行：每行兩個整數X，Y ( 0 ≤ X，Y≤ 100000 )， 表示N個牧區的座標。每個牧區的座標都是不一樣的。

第 N+2 行到第 2*N+1 行：每行包括N個數字 ( 0或1 ) 表示一個對稱鄰接矩陣。

例如，題目描述中的兩個牧場的矩陣描述如下：

8
10 10
15 10
20 10
15 15
20 15
30 15
25 10
30 10
01000000
10111000
01001000
01001000
01110000
00000010
00000101
00000010
 

22.071068