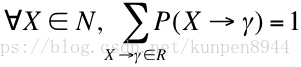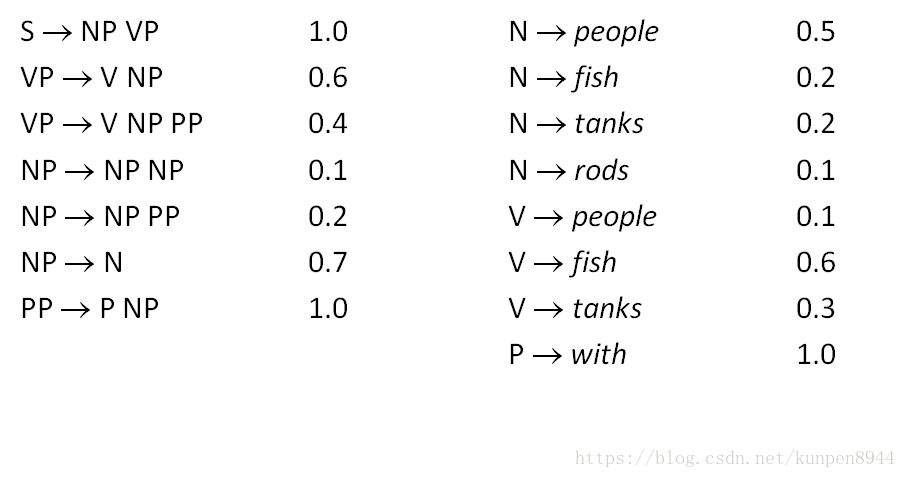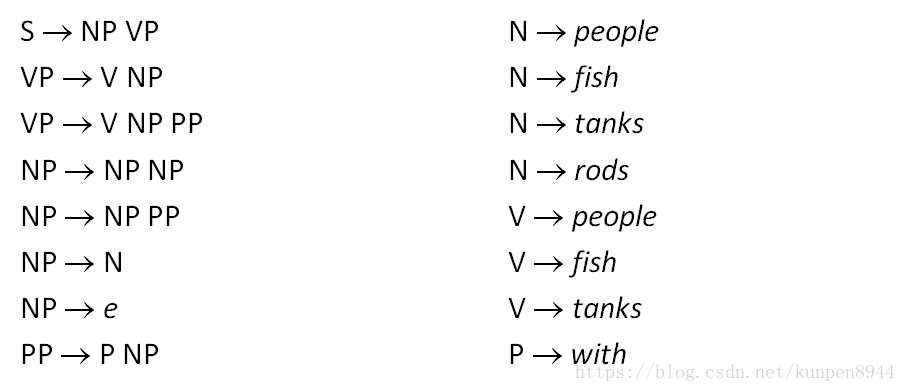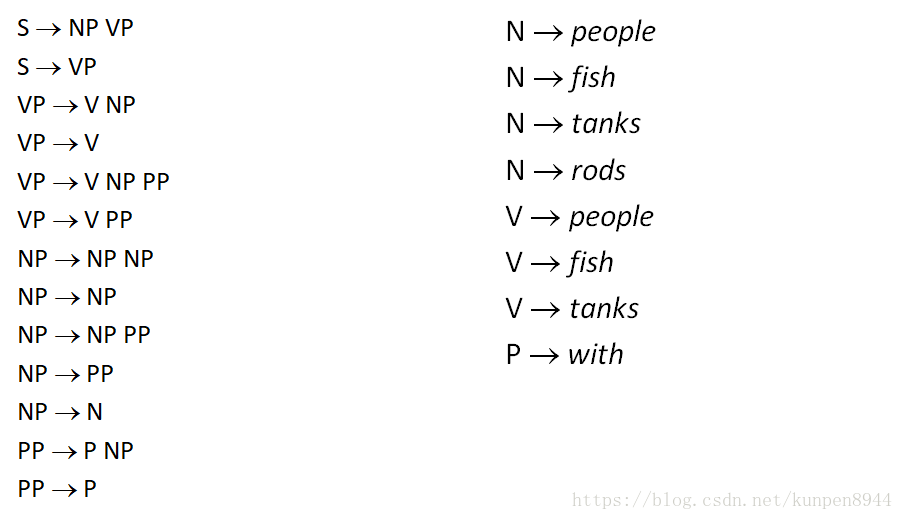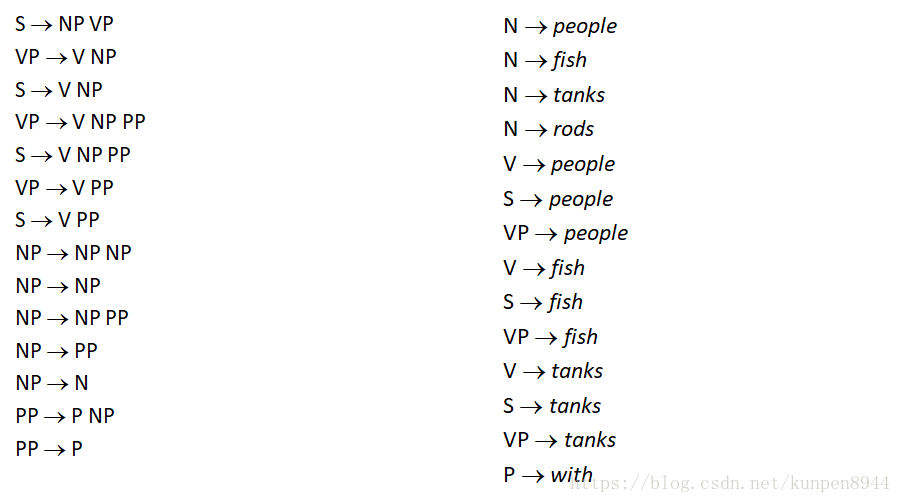一、概率上下文無關文法（(Probabilistic) Context-Free Grammars）

1、上下文無關文法（Context-Free Grammars）

• 我們也可以稱之為片語結構語法(Phrase structure grammars)
• 由四個成分構成G=（T，N，S，R）
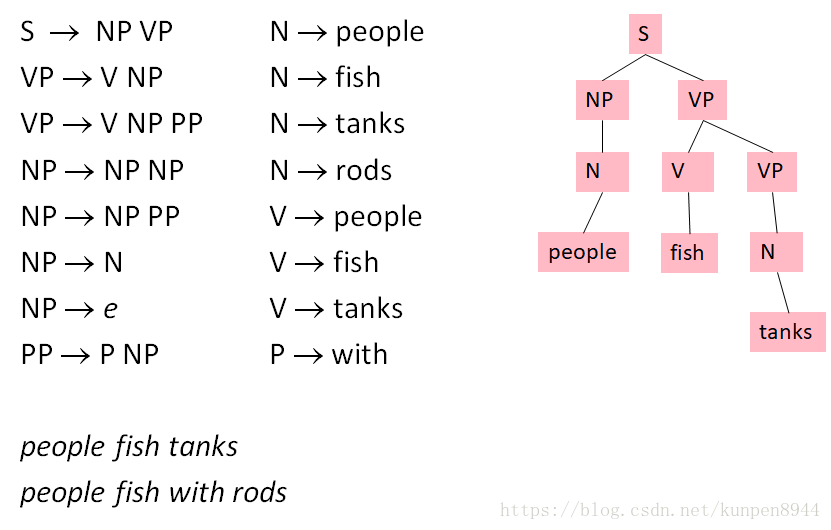
  • T表示最終端（terminal），如下圖粉色部分的子節點
  • N表示非最終端（nonpreterminal），如下圖粉色部分的中間節點
  • S表示開始（S∈N），如下圖粉色部分的根節點
  • R表示一系列的規則，格式為X→γ，其中X∈N，γ∈（N∪T），例子如下圖左邊的規則
    

2、NLP的上下文無關文法（Context-Free Grammars）

• 在NLP的背景下，我們對上下文無關文法的定義進行了一定的修改
• 由六個成分組成G=（T，C，N，S，L，R）
  • T表示最終端（terminal），如上圖粉色部分的子節點，和上面定義一致
  • C表示次終端（preterminal），如上圖粉色部分的子節點的父節點
  • N表示非最終端（nonpreterminal），如上圖粉色部分的中間節點，和上面定義一致
  • S表示開始（S∈N），如上圖粉色部分的根節點，和上面定義一致
  • L表示字典（lexicon），格式為X→x，其中X∈C並且x∈T，如上圖中間的規則
  • R表示一系列的語法規則，格式為X→γ，其中X∈N，γ∈（N∪C），如上圖左邊的規則
• 按照慣例，S表示開始。但是，在統計自然語言中，我們在最開始還會使用另外一個節點（ROOT，TOP）
• 對空序列，我們會用e來表示

3、概率上下文無關文法（Probabilistic/stochastic Context-Free Grammars

• 概率上下文無關文法是上下文無關文法的拓展，在原來的四個元素上增加了一個元素P
• 由五個成分構成G=（T，N，S，R，P）
  • T表示最終端（terminal），如下圖粉色部分的子節點
  • N表示非最終端（nonpreterminal），如下圖粉色部分的中間節點
  • S表示開始（S∈N），如下圖粉色部分的根節點
  • R表示一系列的規則，格式為X→γ，其中X∈N，γ∈（N∪T），例子如下圖左邊的規則
  • P表示概率函式，P的範圍是[0,1]，並且和為1，公式如下：
    
• 文法規則表示如下（增加了概率）：
  
• 概率計算
  • 句法結構樹的概率P(t)計算：生成它的規則的概率的乘積
  • 字串的概率P(s)計算: 有這個字串的句法結構樹的和
    
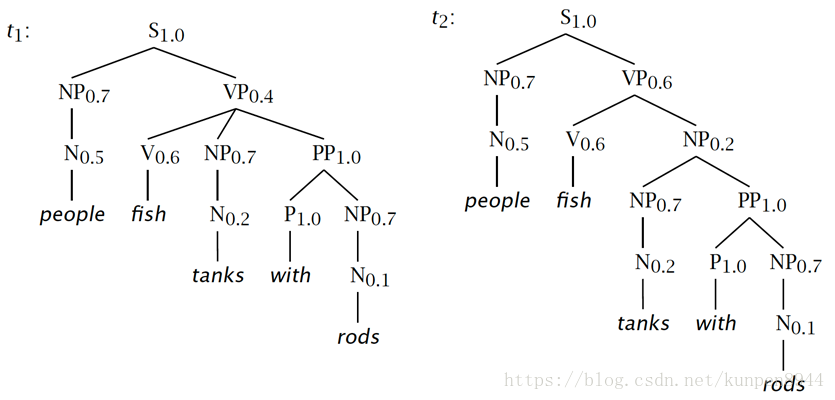
  • 例子：同一個句子的兩個不同的句法結構樹
    
    第一顆樹是動詞附屬（verb attach），概率計算是0.0008232，第二顆樹是名詞附屬(noun attach)，概率計算是0.00024696。字串的概率是兩者之和0.00107016
    

二、語法轉化

1、Chomsky Normal Form

• 我們可以把上下文無關文法（Context-Free Grammars）轉化為Chomsky Normal Form的形式。這種形式不會改變語言本身，但是呈現出的句法結構樹可能會有所不同。可以使得句法分析更加高效。
• 在這種形式中，所有的規則可以轉化為兩種形式：X→Y Z或者是X→w，其中X，Y，Z∈N，w∈T
• 為了實現這種形式，空和一對一的規則（X→Y）會被遞迴地消除
• 一對N的規則（N>2）則會被拆解成新的非終端項（nonterminals）

2、一個轉化的例子

• 初始的上下文無關文法（Context-Free Grammars）
  
• 第一步：消除空（e），由於NP→e，要把這一條刪除同時保留下這一條的資訊，我們可以把左邊規則中箭頭右側出現NP的規則做兩種假設，比如S→NP VP可以改進為兩條規則：S→NP VP和S→VP
  
• 第二步：消除一對一的規則（X→Y）。把一對一的規則轉化為字典形式放在字典（lexicon）中。具體如VP→V，則和字典（lexicon）中V在左側的規則一起生成新規則，如VP→people。並進行迭代消除。
  
  
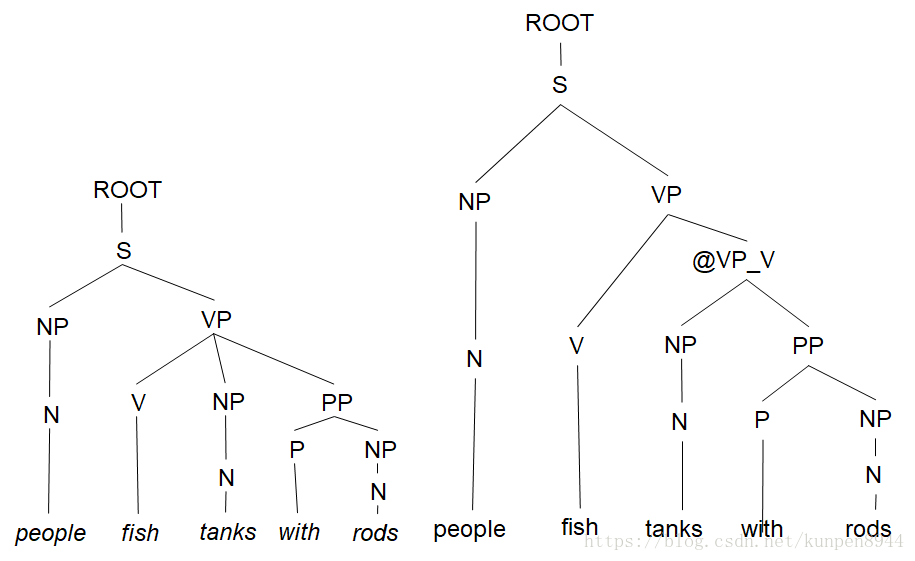
• 第三步：一對N的規則拆成一對二的規則，比如VP→V NP PP拆成兩個規則VP → V @VP_V，@VP_V →NP PP
  
• 在實踐中，完整的Chomsky Normal Form轉換是很痛苦的，一對N的規則拆分是很容易的，但是空（e）和一對一規則的消除非常麻煩。對於上下文無關文法（CFG）句法分析而言，一對N的規則拆分可以幫助建立二叉樹，可以有效降低複雜度。而其他操作不是必要的，充其量就是會使得演算法更乾淨更快而已。下圖右邊就是一對N的規則拆分的句法分析樹。
  
  下圖有顏色的部分表示了同一個短語的不同的四個句法結構樹，第一個是初始，第二個是去掉了空，第三個是去掉了一對一保留了最高的父節點，第四個是去掉了一對一保留了最低的父節點（三四比起來我們更傾向於四，因為可以保留完整的字典）
  

三、CKY演算法

1、演算法介紹

• 我們採用CKY演算法來進行句法分析的時間複雜度是在O（N³）
• 大致來說，計算方法是一個動態規劃的方法。如下圖，從最底層開始，最底層的每一格代表對應的一個單詞，其中包含若干種可能以及對應的概率。次底層的每一格代表的是次終端（preterminal），包含左下角和右下角兩個底層的格子對應的單詞構成的成分（constituency）。
  
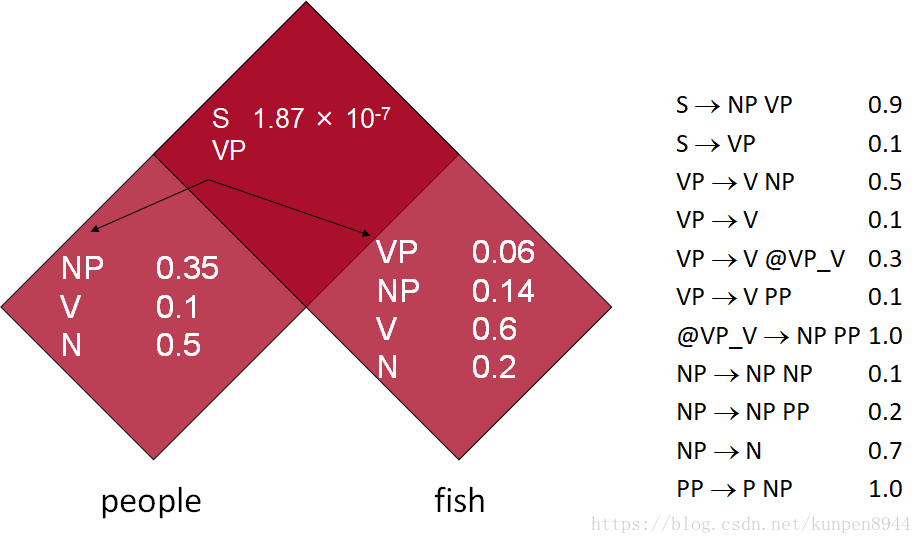
• 舉例而言：下面的例子中有兩個詞people fish，根據字典（lexicon），people對應三種成分（NP，V，N），fish對應四種成分（VP，NP，V，N）。接下來，計算的是兩個單詞組合的成分。根據規則NP→ NP NP，people fish的成分是NP的時候概率是=P(NP→people)*P(NP→fish)*P(NP→ NP NP)=0.350.140.1=0.0049。當有兩種組合的結果成分是相同的時候，我們選取最大的概率放入對應的格子中。
  

2、演算法拓展

• 一對一規則：可以整合進演算法。雖然可能會使得演算法比較混亂，但是不會影響到演算法的複雜度
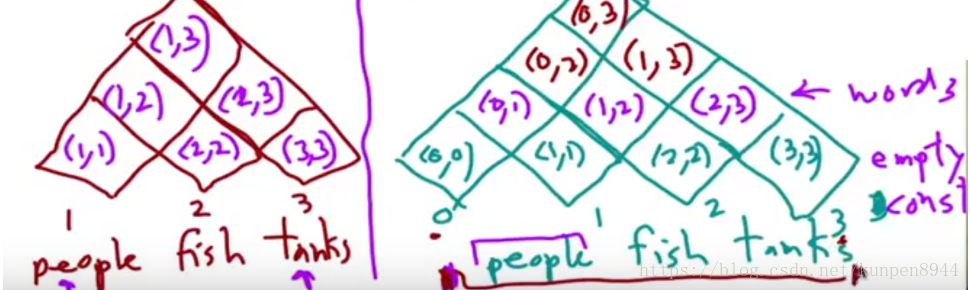
• 空：可以使用fencepost整合進演算法，並且不會影響演算法的複雜度。例子如下，假設有n個單詞，底層構建的時候選用0-n位置，在每個整數位都可以插入空，在整數之間的位置則是單詞。
  
• 二分化，即去掉一對N規則是很有必要的。這是使得演算法複雜度降低從指數級到O（N³）的關鍵，所以在進行CKY演算法之前，一定要進行二分化。

3、程式碼

function CKY(words, grammar) returns [most_probable_parse,prob]
  score = new double[#(words)+1][#(words)+1][#(nonterms)]  //儲存格子中所有可能成分和對應的概率
  back = new Pair[#(words)+1][#(words)+1][#nonterms]] //指標，指出最佳的成分
  
  ****接下來主要處理字典lexicon*****
  for i=0; i<#(words); i++ 對每個單詞
    for A in nonterms 對每個非終端
      if A -> words[i] in grammar 如果A指向對應的單詞的話，就在score中儲存
        score[i][i+1][A] = P(A -> words[i])
    //handle unaries 下面部分處理一對一規則
    boolean added = true
    while added 
      added = false
      for A, B in nonterms
        if score[i][i+1][B] > 0 && A->B in grammar 一對一規則搜尋
          prob = P(A->B)*score[i][i+1][B]
          if prob > score[i][i+1][A] 判斷一對一的概率是否會比原來的大，如果是的話就覆蓋原來的概率
            score[i][i+1][A] = prob
            back[i][i+1][A] = B
            added = true
            
   ****接下來主要處理語法規則*****
	for span = 2 to #(words)
	  for begin = 0 to #(words)- span
	    end = begin + span
	    for split = begin+1 to end-1 對一串語句而言，選擇二分的節點
	      for A,B,C in nonterms
	            prob=score[begin][split][B]*score[split][end][C]*P(A->BC) 計算對應的概率
	        if prob > score[begin][end][A] 如果概率大於原來的概率就覆蓋，修改back指標
	          score[begin]end][A] = prob
	          back[begin][end][A] = new Triple(split,B,C)
	    //handle unaries  下面部分處理一對一規則
	    boolean added = true
	    while added
	      added = false
	      for A, B in nonterms
	        prob = P(A->B)*score[begin][end][B];
	        if prob > score[begin][end][A]  判斷一對一的概率是否會比原來的大，如果是的話就覆蓋原來的概率
	          score[begin][end][A] = prob
	          back[begin][end][A] = B
	          added = true
return buildTree(score, back)

四、例子

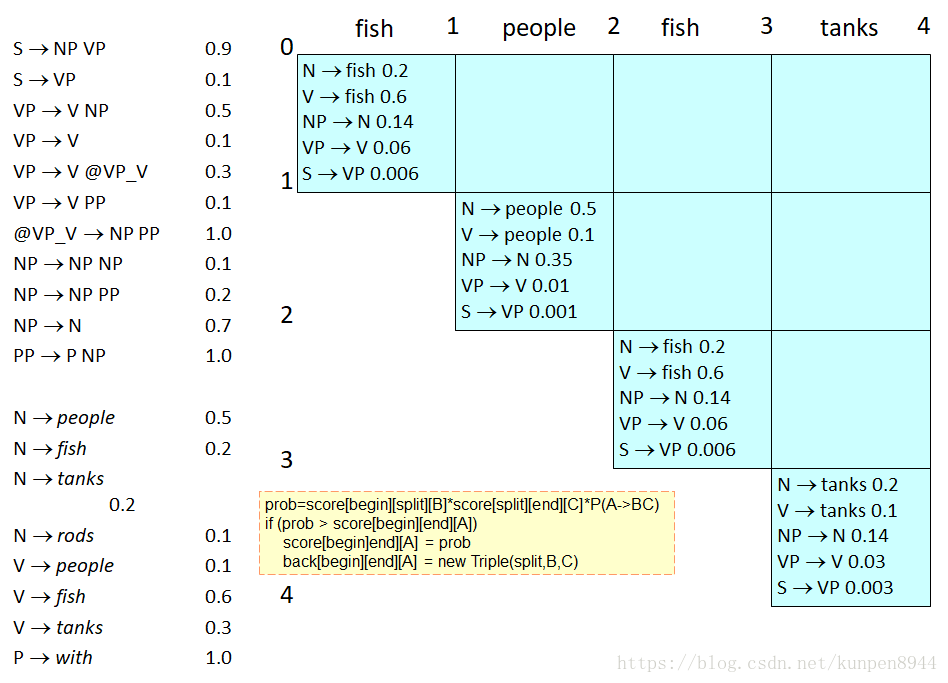
• 沒有空（e）的規則
  
• socre陣列，行數和列數都是單詞數
  
• 第一步：利用lexicon在score中寫入規則：以0-1的fish為例，對應的lexicon是N→fish 0.2和V→fish 0.6（下面每一步的結果都在下一步的圖中給出）
  
• 第二步：處理字典部分的一對一規則。以0-1的fish為例，已有的lexicon是N→fish 0.2和V→fish 0.6。可以找到一對一語法規則VP→V（概率是0.60.1），NP→N（概率是0.70.2），因為原來的概率是0，所以對其直接進行覆蓋。對一共四個的語法規則再迭代，可以找到一對一的語法規則S→VP（概率為0.60.10.1）
  
• 第三步：處理語法規則。計算次底層的概率，以fish和people為例
  • NP -> NP NP : P(NP->N)*P(NP->N)*P(NP -> NP NP)=0.14*0.35*0.1
  • VP ->V NP: P(V->fish)*P(NP->N)*P(VP ->V NP)=0.6*0.35*0.5
  • S->NP VP: P(NP->N)*P(VP->V)*P(S->NP VP)=0.14*0.01*0.9=0.00126
    
• 第四步：處理一對一語法規則。以fish和people為例，S->VP:P(VP ->V NP)*P(S->VP)=0.6*0.35*0.5*0.1=0.0105，比之前算出的概率大，覆蓋S的概率
  
• 第五步，計算第三層的語法規則。以fish people fish為例，可能存在兩種可能：二元分割點在1，二元分割點在2。分別計算可能的概率，並進行一對一規則的處理。
  
• 第六步：計算最後一層。
  
• 結果
  

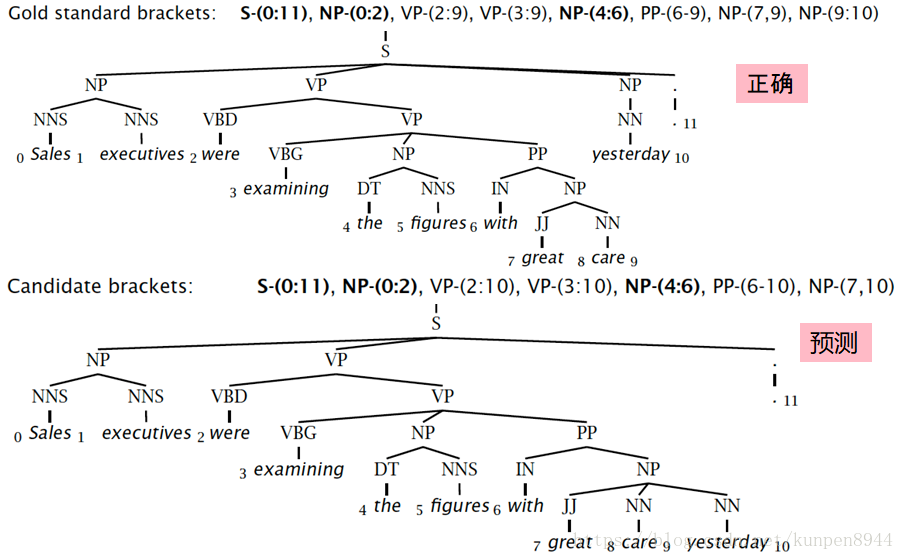
五、成分句法分析評估方法

• 計算方法：對每一格單詞間隔進行索引，將每個巢狀的成分，從上到小從左到右用索引表示出來。比如下面的句法分析，第一層的S是0-11，接下來NP是0-2，VP是2-9。
  
  基於上面的成分索引，計算對應的precision和recall。標註評價是另外給出的一個正確率。
  
• PCFGs模型的優點